CAT LR Puzzles Questions PDF [Most Important]
CAT LR Puzzles is one of the most important topics in the CAT Logical Reasoning & Data Interpretation Section. You can check out these CAT LR Puzzles Questions from the CAT previous year papers. This article will look into some very important LR Puzzles questions PDF(with solutions) for CAT. If you want to practice these questions, you can download this CAT LR Puzzles Questions PDF (most important) along with the solutions below, which is completely Free.
Download LR Puzzles Questions for CAT
Instructions
Ten objects o1, o2, …, o10 were distributed among Amar, Barat, Charles, Disha, and Elise. Each item went to exactly one person. Each person got exactly two of the items, and this pair of objects is called her/his bundle.
The following table shows how each person values each object.

The value of any bundle by a person is the sum of that person’s values of the objects in that bundle. A person X envies another person Y if X values Y’s bundle more than X’s own bundle.
For example, hypothetically suppose Amar’s bundle consists of o1 and o2, and Barat’s bundle consists of o3 and o4. Then Amar values his own bundle at 4 + 9 = 13 and Barat’s bundle at 9 + 3 = 12. Hence Amar does not envy Barat. On the other hand, Barat values his own bundle at 7 + 5 = 12 and Amar’s bundle at 5 + 9 = 14. Hence Barat envies Amar.
The following facts are known about the actual distribution of the objects among the five people.
1. If someone’s value for an object is 10, then she/he received that object.
2. Objects o1, o2, and o3 were given to three different people.
3. Objects o1 and o8 were given to different people.
4. Three people value their own bundles at 16. No one values her/his own bundle at a number higher than 16.
5. Disha values her own bundle at an odd number. All others value their own bundles at an even number.
6. Some people who value their own bundles less than 16 envy some other people who value their own bundle at 16. No one else envies others.
Question 1: What BEST can be said about the distribution of object o1?
a) o1 was given to Disha
b) o1 was given to Charles
c) o1 was given to Charles, Disha, or Elise
d) o1 was given to Charles or Disha
1) Answer (A)
Solution:
We have the following table :

o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1 :
o1 is given to Elise
Now the total valuation of Elise = 12
Valuation of Disha is an odd number
So we can say Amar , Bharat and Charles values their bundles at 16 .
So for Bharat the valuation to be 16, o7 will be given to him
so we get
Bharat – o9 and o7 and Elise -o10 and o1
For charles to have valuation 16
the only way = 8+8
so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together )
Now for Amart to have a valuation of 16
the only way possible = 9+7
Now so we can say
Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6
So if Disha receives o4 and o6
The valuation of Disha will be 5+3 =8 which is not an odd number
so this case is discarded.
Case 2 Elise receives o5 or o7 .
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat
received o9 and we know the evaluation of Bharat is an even number and
the minimum even number possible for valuation of Bharat is 16 and no
one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5 .
So we have
Bharat – o9 ,o7
Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha .
Now As per Amar
he values Bharat at 17 so he envy him
So Amar will value his bundle less than 16
So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 .
Now
o8 will be given to Charu, and he cannot have o1 , also he cannot have
o2 because if he has o2 he will value Bharat’s bundle as 17 and will
envy him which is not possible so Charu will have o3,o8
Now Amar will have o2 and Disha will have o1.
Now
Amar will not have o4 because in that case Charles will envy Amar and
is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following :
Amar – o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
So o1 is given to Disha
Question 2: Object o5 was given to
a) Disha
b) Elise
c) Amar
d) Charles
2) Answer (B)
Solution:
We have the following table :

o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1 :
o1 is given to Elise
Now the total valuation of Elise = 12
Valuation of Disha is an odd number
So we can say Amar , Bharat and Charles values their bundles at 16 .
So for Bharat the valuation to be 16, o7 will be given to him
so we get
Bharat – o9 and o7 and Elise -o10 and o1
For charles to have valuation 16
the only way = 8+8
so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together )
Now for Amart to have a valuation of 16
the only way possible = 9+7
Now so we can say
Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6
So if Disha receives o4 and o6
The valuation of Disha will be 5+3 =8 which is not an odd number
so this case is discarded.
Case 2 Elise receives o5 or o7 .
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat
received o9 and we know the evaluation of Bharat is an even number and
the minimum even number possible for valuation of Bharat is 16 and no
one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5 .
So we have
Bharat – o9 ,o7
Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha .
Now As per Amar
he values Bharat at 17 so he envy him
So Amar will value his bundle less than 16
So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 .
Now
o8 will be given to Charu, and he cannot have o1 , also he cannot have
o2 because if he has o2 he will value Bharat’s bundle as 17 and will
envy him which is not possible so Charu will have o3,o8
Now Amar will have o2 and Disha will have o1.
Now
Amar will not have o4 because in that case Charles will envy Amar and
is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following :
Amar – o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
o5 is given to Elise
Question 3: Object o4 was given to
a) Elise
b) Barat
c) Charles
d) Disha
3) Answer (D)
Solution:
We have the following table :

o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1 :
o1 is given to Elise
Now the total valuation of Elise = 12
Valuation of Disha is an odd number
So we can say Amar , Bharat and Charles values their bundles at 16 .
So for Bharat the valuation to be 16, o7 will be given to him
so we get
Bharat – o9 and o7 and Elise -o10 and o1
For charles to have valuation 16
the only way = 8+8
so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together )
Now for Amart to have a valuation of 16
the only way possible = 9+7
Now so we can say
Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6
So if Disha receives o4 and o6
The valuation of Disha will be 5+3 =8 which is not an odd number
so this case is discarded.
Case 2 Elise receives o5 or o7 .
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat
received o9 and we know the evaluation of Bharat is an even number and
the minimum even number possible for valuation of Bharat is 16 and no
one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5 .
So we have
Bharat – o9 ,o7
Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha .
Now As per Amar
he values Bharat at 17 so he envy him
So Amar will value his bundle less than 16
So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 .
Now
o8 will be given to Charu, and he cannot have o1 , also he cannot have
o2 because if he has o2 he will value Bharat’s bundle as 17 and will
envy him which is not possible so Charu will have o3,o8
Now Amar will have o2 and Disha will have o1.
Now
Amar will not have o4 because in that case Charles will envy Amar and
is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following :
Amar – o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
o4 is given to Disha
Question 4: What is Amar’s value for his own bundle?
4) Answer: 12
Solution:
We have the following table :

o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1 :
o1 is given to Elise
Now the total valuation of Elise = 12
Valuation of Disha is an odd number
So we can say Amar , Bharat and Charles values their bundles at 16 .
So for Bharat the valuation to be 16, o7 will be given to him
so we get
Bharat – o9 and o7 and Elise -o10 and o1
For charles to have valuation 16
the only way = 8+8
so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together )
Now for Amart to have a valuation of 16
the only way possible = 9+7
Now so we can say
Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6
So if Disha receives o4 and o6
The valuation of Disha will be 5+3 =8 which is not an odd number
so this case is discarded.
Case 2 Elise receives o5 or o7 .
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat
received o9 and we know the evaluation of Bharat is an even number and
the minimum even number possible for valuation of Bharat is 16 and no
one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5 .
So we have
Bharat – o9 ,o7
Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha .
Now As per Amar
he values Bharat at 17 so he envy him
So Amar will value his bundle less than 16
So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 .
Now
o8 will be given to Charu, and he cannot have o1 , also he cannot have
o2 because if he has o2 he will value Bharat’s bundle as 17 and will
envy him which is not possible so Charu will have o3,o8
Now Amar will have o2 and Disha will have o1.
Now
Amar will not have o4 because in that case Charles will envy Amar and
is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following :
Amar – o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
Amar’s own valuation = 9+3 =12
Question 5: Who among the following envies someone else?
a) Barat
b) Charles
c) Amar
d) Elise
5) Answer (C)
Solution:
We have the following table :

o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1 :
o1 is given to Elise
Now the total valuation of Elise = 12
Valuation of Disha is an odd number
So we can say Amar , Bharat and Charles values their bundles at 16 .
So for Bharat the valuation to be 16, o7 will be given to him
so we get
Bharat – o9 and o7 and Elise -o10 and o1
For charles to have valuation 16
the only way = 8+8
so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together )
Now for Amart to have a valuation of 16
the only way possible = 9+7
Now so we can say
Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6
So if Disha receives o4 and o6
The valuation of Disha will be 5+3 =8 which is not an odd number
so this case is discarded.
Case 2 Elise receives o5 or o7 .
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat
received o9 and we know the evaluation of Bharat is an even number and
the minimum even number possible for valuation of Bharat is 16 and no
one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5 .
So we have
Bharat – o9 ,o7
Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha .
Now As per Amar
he values Bharat at 17 so he envy him
So Amar will value his bundle less than 16
So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 .
Now
o8 will be given to Charu, and he cannot have o1 , also he cannot have
o2 because if he has o2 he will value Bharat’s bundle as 17 and will
envy him which is not possible so Charu will have o3,o8
Now Amar will have o2 and Disha will have o1.
Now
Amar will not have o4 because in that case Charles will envy Amar and
is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following :
Amar – o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
So Amar envies someone else
Checkout: CAT Free Practice Questions and Videos
Question 6: What BEST can be said about object o8?
a) o8 was given to Amar, Charles, or Disha
b) o8 was given to Disha
c) o8 was given to Charles
d) o8 was given to Charles or Disha
6) Answer (C)
Solution:
We have the following table :

o10 is given to Elise and o9 is given to Bharat .
Now as Elise values his own bundle at an even number so the only two objects which can be given to Elise is o1 or o5 or o7.
Case 1 :
o1 is given to Elise
Now the total valuation of Elise = 12
Valuation of Disha is an odd number
So we can say Amar , Bharat and Charles values their bundles at 16 .
So for Bharat the valuation to be 16, o7 will be given to him
so we get
Bharat – o9 and o7 and Elise -o10 and o1
For charles to have valuation 16
the only way = 8+8
so we can say o8 is given to charles along with either o2 or o3 .(o1 and o8 cannot be together )
Now for Amart to have a valuation of 16
the only way possible = 9+7
Now so we can say
Amar will receive either o2 or o3 and o5 .
Now we are left with 04 and o6
So if Disha receives o4 and o6
The valuation of Disha will be 5+3 =8 which is not an odd number
so this case is discarded.
Case 2 Elise receives o5 or o7 .
Now Valuation of Elise = 16 .
And Elise receives o10 and o5/o7.
Bharat received o9 and we know the evaluation of Bharat is an even number and the minimum even number possible for valuation of Bharat is 16 and no one can have evaluation more than 16 so Bharat received o7 .
So Elise received o5 .
So we have
Bharat – o9 ,o7
Elise -o10,o5.
Now as we know o1 ,o2 and o3 are given to three different persons so they are Amar, Charles and Disha .
Now As per Amar
he values Bharat at 17 so he envy him
So Amar will value his bundle less than 16
So the only possibility for Amar to value his bundle less than 16 = 12 =9+3.
Now we can say Charu will have 16 as his own valuation so he will get 8+8 .
Now o8 will be given to Charu, and he cannot have o1 , also he cannot have o2 because if he has o2 he will value Bharat’s bundle as 17 and will envy him which is not possible so Charu will have o3,o8
Now Amar will have o2 and Disha will have o1.
Now Amar will not have o4 because in that case Charles will envy Amar and is not possible so we can say Amar will have o6 and Disha will have o4.
So we have the following :
Amar – o2,o6
Bharat -o9,o7
Charu -o3,o8
Disha o1,o4
Elise -o10,o5
So o8 is given to Charu.
Instructions
Sixteen patients in a hospital must undergo a blood test for a disease. It is known that exactly one of them has the disease. The hospital has only eight testing kits and has decided to pool blood samples of patients into eight vials for the tests. The patients are numbered 1 through 16, and the vials are labelled A, B, C, D, E, F, G, and H. The following table shows the vials into which each patient’s blood sample is distributed.
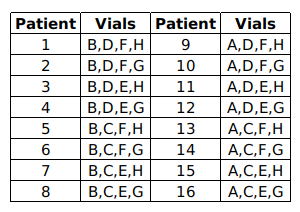
If a patient has the disease, then each vial containing his/her blood sample will test positive. If a vial tests positive, one of the patients whose blood samples were mixed in the vial has the disease. If a vial tests negative, then none of the patients whose blood samples were mixed in the vial has the disease.
Question 7: Suppose one of the lab assistants accidentally mixed two patients’ blood samples before they were distributed to the vials. Which of the following correctly represents the set of all possible numbers of positive test results out of the eight vials?
a) {5,6,7,8}
b) {4,5,6,7}
c) {4,5,6,7,8}
d) {4,5}
7) Answer (C)
Solution:
Let one of the patients, patient 1 or patient 16 has the disease and his blood is mixed with other them all 8 vials will tests positive. ⇒
8 has to be one of the answers.
If patient 2 and patients 16’s blood is mixed of one of them has the disease then 7 of the 8 vials will test positive. So 7 has to be there
in the option.
If 1 has the disease and 1, 7 are mixed then 6 out the 8 vials tests positive.
IF 1 has the disease and 1,9 are mixed then 5 of the 8 vials tests positive,
Now, let us assume that patient 1 has the disease if his blood is not mixed,
then 4 vials will definitely show positive.
Hence 3 is the correct answer.
Question 8: Which of the following combinations of test results is NOT possible?
a) Vials A and E positive, vials C and D negative
b) Vial B positive, vials C, F and H negative
c) Vials A and G positive, vials D and E negative
d) Vials B and D positive, vials F and H negative
8) Answer (A)
Solution:
The patients in
Vial A: 9, 10, 11, 12, 13, 14, 15, 16
Vial B: 1, 2, 3, 4, 5, 6, 7, 8.
Vial C: 5,6,7,8,13,14,15,16
Vial D:1,2,3,4,9,10,11,12
Vial E:3,4,7,8,11,12,15,16
Vial F:1,2,5,6,9,10,13,14
Vial G:2,4,6,8,10,12,14,16
Vial H:1,3,5,7,9,11,13,15
If vials C and D negative then no patient could test negative. Hence A is correct answer.
Question 9: Suppose vial A tests positive and vials D and G test negative. Which of the following vials should we test next to identify the patient with the disease?
a) Vial B
b) Vial E
c) Vial C
d) Vial H
9) Answer (B)
Solution:
The patients in
Vial A: 9, 10, 11, 12, 13, 14, 15, 16
Vial B: 1, 2, 3, 4, 5, 6, 7, 8.
Vial C: 5,6,7,8,13,14,15,16
Vial D:1,2,3,4,9,10,11,12
Vial E:3,4,7,8,11,12,15,16
Vial F:1,2,5,6,9,10,13,14
Vial G:2,4,6,8,10,12,14,16
Vial H:1,3,5,7,9,11,13,15
Suppose vial A tests positive and vials D and G test negative then the patient who tested positive must be one of patient 13 or 15.
Patient 13 or 15 are not present in vial B. So, A is not the answer.
Both patients present in vial C. Even if tested positive or negative we can’t know who has got the disease. So, C is not the answer.
Both patients present in vial H. Even if tested positive or negative we can’t know who has got the disease. So, H is not the answer.
only patient 15 is present in vial E, if tested positive then patient 15 has the disease else patient 13 as disease.
Hence Option 2 is correct.
Question 10: Suppose vial C tests positive and vials A, E and H test negative. Which patient has the disease?
a) Patient 14
b) Patient 8
c) Patient 6
d) Patient 2
10) Answer (C)
Solution:
The patients in
Vial A: 9, 10, 11, 12, 13, 14, 15, 16
Vial B: 1, 2, 3, 4, 5, 6, 7, 8.
Vial C: 5,6,7,8,13,14,15,16
Vial D:1,2,3,4,9,10,11,12
Vial E:3,4,7,8,11,12,15,16
Vial F:1,2,5,6,9,10,13,14
Vial G:2,4,6,8,10,12,14,16
Vial H:1,3,5,7,9,11,13,15
If vial C tests positive and vials A, E and H test negative then Patient 6 must have disease as all other patients in Vial C expect patient 6 are present in at least one of A, E, H.




![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)
