CAT Averages and Mixtures Questions PDF

Averages and Mixtures questions are very important in the Arithmetic concept of the CAT Quants section. These questions are not very tough; make sure you are aware of all the Important Formulas in CAT Averages and Mixtures. You can also check out these CAT Averages and Mixture questions from the CAT Previous year papers. Practice a good number of questions in CAT Average and Mixture so that you can easily answer these questions in the exam. This post will look into some important Averages and Mixtures Questions for CAT. These are a good source of practice for CAT 2022 preparation; If you want to practice these questions, you can download these Important Average and Mixture Questions for CAT (with detailed answers) PDF along with the video solutions below, which is completely Free.

Download Averages and Mixtures Questions for CAT

Enroll to CAT Mocks at just Rs. 299

Question 1: Consider the set S = {2, 3, 4, …., 2n+1}, where n is a positive integer larger than 2007. Define X as the average of the odd integers in S and Y as the average of the even integers in S. What is the value of X – Y ?

a) 0

b) 1

c) (1/2)*n

d) (n+1)/2n

e) 2008

1) Answer (B)

View Video Solution

Solution:

The odd numbers in the set are 3, 5, 7, …2n+1

Sum of the odd numbers = 3+5+7+…+(2n+1) = $n^2 + 2n$

Average of odd numbers = $n^2 + 2n$/n = n+2

Sum of even numbers = 2 + 4 + 6 + … + 2n = 2(1+2+3+…+n) = 2*n*(n+1)/2 = n(n+1)

Average of even numbers = n(n+1)/n = n+1

So, difference between the averages of even and odd numbers = 1

Question 2: Three classes X, Y and Z take an algebra test.
The average score in class X is 83.
The average score in class Y is 76.
The average score in class Z is 85.
The average score of all students in classes X and Y together is 79.
The average score of all students in classes Y and Z together is 81.
What is the average for all the three classes?

a) 81

b) 81.5

c) 82

d) 84.5

2) Answer (B)

View Video Solution

Solution:

Let x , y and z be no. of students in class X, Y ,Z respectively.

From 1st condition we have

83*x+76*y = 79*x+79*y which give 4x = 3y.

Next we have 76*y + 85*z = 81(y+z) which give 4z = 5y .

Now overall average of all the classes can be given as $\frac{83x+76y+85z}{x+y+z}$

Substitute the relations in above equation we get,

$\frac{83x+76y+85z}{x+y+z}$  = (83*3/4 + 76 + 85*5/4)/(3/4 + 1 + 5/4) = 978/12 = 81.5

Question 3: Consider a sequence of seven consecutive integers. The average of the first five integers is n. The average of all the seven integers is:
[CAT 2000]

a) n

b) n+1

c) kn, where k is a function of n

d) n+(2/7)

3) Answer (B)

View Video Solution

Solution:

The first five numbers could be n-2, n-1, n, n+1, n+2. The next two number would then be, n+3 and n+4, in which case, the average of all the 7 numbers would be $\frac{(5n+2n+7)}{7}$ = n+1

Question 4: The average marks of a student in 10 papers are 80. If the highest and the lowest scores are not considered, the average is 81. If his highest score is 92, find the lowest.

a) 55

b) 60

c) 62

d) Cannot be determined

4) Answer (B)

View Video Solution

Solution:

Total marks = 80 x 10 = 800
Total marks except highest and lowest marks = 81 x 8 = 648
So Summation of highest marks and lowest marks will be = 800 – 648 = 152
When highest marks is 92, lowest marks will be = 152-92 = 60

Instructions

DIRECTIONS for the following two questions: The following table presents the sweetness of different items relative to sucrose, whose sweetness is taken to be 1.00.

Question 5: What is the maximum amount of sucrose (to the nearest gram) that can be added to one-gram of saccharin such that the final mixture obtained is atleast 100 times as sweet as glucose?

a) 7

b) 8

c) 9

d) 100

5) Answer (B)

View Video Solution

Solution:

For the mixture to be 100 times as sweet as glucose, its sweetness relative to the mixture should be at least 74.

1 gm of saccharin = 675

Let the number of grams of sucrose to be added be N. Thus, the total weight of the mixture = N + 1.

So, (675 + N) / (N+1) = 74

=> 675 + N = 74N + 74

=> 601 = 73N => N = 8.23

When N=9, sweetness will be S = (675+9)/10 = 684/10 = 68.4

When N=8, sweetness will be S = (675+8)/9 = 683/9 = 75.8

So, option b) is the correct answer.

Question 6: Approximately how many times sweeter than sucrose is a mixture consisting of glucose, sucrose and fructose in the ratio of 1: 2: 3?

a) 1.3

b) 1

c) 0.6

d) 2.3

6) Answer (A)

View Video Solution

Solution:

The relative sweetness of the mixture is (1*0.74 + 2*1 + 3*1.7) / (1+2+3) = 7.84/6 = 1.30

Option a) is the correct answer.

Checkout: CAT Free Practice Questions and Videos

Question 7: A class consists of 20 boys and 30 girls. In the mid-semester examination, the average score of the girls was 5 higher than that of the boys. In the final exam, however, the average score of the girls dropped by 3 while the average score of the entire class increased by 2. The increase in the average score of the boys is

a) 9.5

b) 10

c) 4.5

d) 6

7) Answer (A)

View Video Solution

Solution:

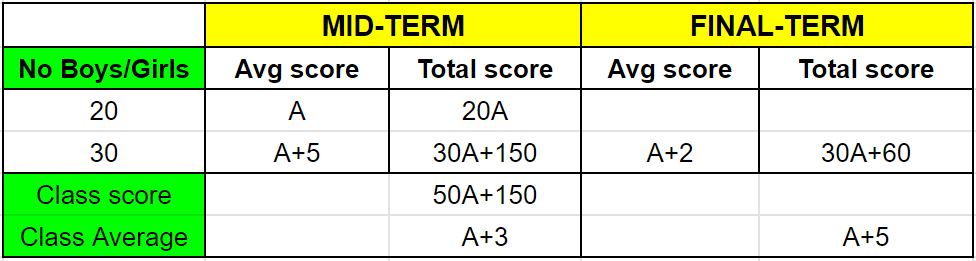
Let, the average score of boys in the mid semester exam is A.
Therefore, the average score of girls in the mid semester exam be A+5.
Hence, the total marks scored by the class is $20\times (A) + 30\times (A+5) = 50\times A + 150$

The average score of the entire class is $\dfrac{(50\times A + 150)}{50} = A + 3$

wkt, class average increased by 2, class average in final term $= (A+3) + 2 = A + 5$

Given, that score of girls dropped by 3, i.e $(A+5)-3 = A+2$
Total score of girls in final term $= 30\times(A+2) = 30A + 60$

Total class score in final term $= (A + 5)\times50 = 50A + 250$

the total marks scored by the boys is $(50A + 250) – (30A – 60) = 20A + 190$
Hence, the average of the boys in the final exam is $\dfrac{(20G + 190)}{20} = A + 9.5$

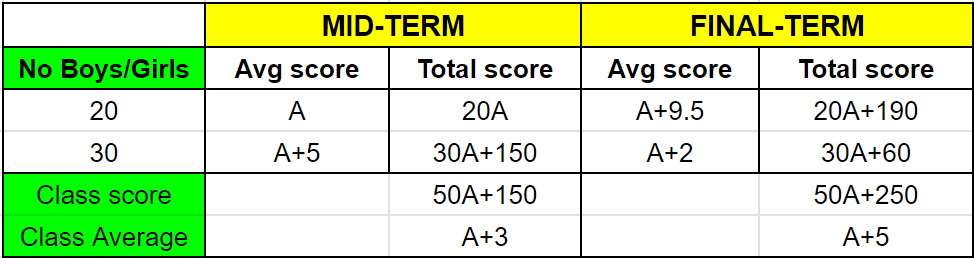
Hence, the increase in the average marks of the boys is $(A+9.5) – A = 9.5$

Question 8: Bottle 1 contains a mixture of milk and water in 7: 2 ratio and Bottle 2 contains a mixture of milk and water in 9: 4 ratio. In what ratio of volumes should the liquids in Bottle 1 and Bottle 2 be combined to obtain a mixture of milk and water in 3:1 ratio?

a) 27:14

b) 27:13

c) 27:16

d) 27:18

8) Answer (B)

View Video Solution

Solution:

The ratio of milk and water in Bottle 1 is 7:2 and the ratio of milk and water in Bottle 2 is 9:4
Therefore, the proportion of milk in Bottle 1 is $\frac{7}{9}$ and the proportion of milk in Bottle 2 is $\frac{9}{13}$

Let the ratio in which they should be mixed be equal to X:1.

Hence, the total volume of milk is $\frac{7X}{9}+\frac{9}{13}$
The total volume of water is $\frac{2X}{9}+\frac{4}{13}$
They are in the ratio 3:1

Hence, $\frac{7X}{9}+\frac{9}{13} = 3*(\frac{2X}{9}+\frac{4}{13})$
Therefore, $91X+81=78X+108$

Therefore $X = \frac{27}{13}$

Question 9: The average height of 22 toddlers increases by 2 inches when two of them leave this group. If the average height of these two toddlers is one-third the average height of the original 22, then the average height, in inches, of the remaining 20 toddlers is

a) 30

b) 28

c) 32

d) 26

9) Answer (C)

View Video Solution

Solution:

Let the average height of 22 toddlers be 3x.
Sum of the height of 22 toddlers = 66x
Hence average height of the two toddlers who left the group = x
Sum of the height of the remaining 20 toddlers = 66x – 2x = 64x
Average height of the remaining 20 toddlers = 64x/20 = 3.2x
Difference = 0.2x = 2 inches => x = 10 inches
Hence average height of the remaining 20 toddlers = 3.2x = 32 inches

Question 10: Consider three mixtures — the first having water and liquid A in the ratio 1:2, the second having water and liquid B in the ratio 1:3, and the third having water and liquid C in the ratio 1:4. These three mixtures of A, B, and C, respectively, are further mixed in the proportion 4: 3: 2. Then the resulting mixture has

a) The same amount of water and liquid B

b) The same amount of liquids B and C

c) More water than liquid B

d) More water than liquid A

10) Answer (C)

View Video Solution

Solution:

The proportion of water in the first mixture is $\frac{1}{3}$
The proportion of Liquid A in the first mixture is $\frac{2}{3}$

The proportion of water in the second mixture is $\frac{1}{4}$
The proportion of Liquid B in the second mixture is $\frac{3}{4}$

The proportion of water in the third mixture is $\frac{1}{5}$
The proportion of Liquid C in the third mixture is $\frac{4}{5}$

As they are mixed in the ratio 4:3:2, the final amount of water is $4 \times \frac{1}{3} + 3 \times \frac{1}{4} + 2 \times \frac{1}{5} = \frac{149}{60}$
The final amount of Liquid A in the mixture is $4\times\frac{2}{3} = \frac{8}{3}$
The final amount of Liquid B in the mixture is $3\times\frac{3}{4} = \frac{9}{4}$
The final amount of Liquid C in the mixture is $2\times\frac{4}{5} = \frac{8}{5}$

Hence, the ratio of Water : A : B : C in the final mixture is $\frac{149}{60}:\frac{8}{3}:\frac{9}{4}:\frac{8}{5} = 149:160:135:96$

From the given choices, only option C  is correct.

Question 11: A trader sells 10 litres of a mixture of paints A and B, where the amount of B in the mixture does not exceed that of A. The cost of paint A per litre is Rs. 8 more than that of paint B. If the trader sells the entire mixture for Rs. 264 and makes a profit of 10%, then the highest possible cost of paint B, in Rs. per litre, is

a) 16

b) 26

c) 20

d) 22

11) Answer (C)

View Video Solution

Solution:

Let the price of paint B be x.
Price of paint A = x+8

We know that the amount of paint B in the mixture does not exceed the amount of paint A. Therefore, paint B can at the maximum compose 50% of the mixture.

The seller sells 10 litres of paint at Rs.264 earning a profit of 10%.
=> The cost price of 10 litres of the paint mixture = Rs. 240

Therefore, the cost of 1 litre of the mixture = Rs.24

We have to find the highest possible cost of paint B.
When we increase the cost of paint B, the cost of paint A will increase too. If the cost price of the mixture is closer to the cost of paint B, then the amount of paint B present in the mixture should be greater than the amount of paint A present in the mixture.
The highest possible cost of paint B will be obtained when the volumes of paint A and paint B in the mixture are equal.

=> (x+x+8)/2 = 24
2x = 40
x = Rs. 20

Therefore, option C is the right answer.

Question 12: A CAT aspirant appears for a certain number of tests. His average score increases by 1 if the first 10 tests are not considered, and decreases by 1 if the last 10 tests are not considered. If his average scores for the first 10 and the last 10 tests are 20 and 30, respectively, then the total number of tests taken by him is

12) Answer: 60

View Video Solution

Solution:

Let the total number of tests be ‘n’ and the average by ‘A’
Total score = n*A
When 1st 10 tests are excluded, decrease in total value of scores = (nA – 20 * 10) = (nA – 200)
Also, (n – 10)(A + 1) = (nA – 200)
On solving, we get 10A – n = 190……….(i)
When last 10 tests are excluded, decrease in total value of scores = (nA – 30 * 10) = (nA – 300)
Also, (n – 10)(A – 1) = (nA – 300)
On solving, we get 10A + n = 310……….(ii)
From (i) and (ii), we get n = 60
Hence, 60 is the correct answer.

Question 13: A jar contains a mixture of 175 ml water and 700 ml alcohol. Gopal takes out 10% of the mixture and substitutes it by water of the same amount. The process is repeated once again. The percentage of water in the mixture is now

a) 30.3

b) 35.2

c) 25.4

d) 20.5

13) Answer (B)

View Video Solution

Solution:

Final quantity of alcohol in the mixture = $\dfrac{700}{700+175}*(\dfrac{90}{100})^2*[700+175]$ = 567 ml

Therefore, final quantity of water in the mixture = 875 – 567 = 308 ml

Hence, we can say that the percentage of water in the mixture = $\dfrac{308}{875}\times 100$ = 35.2 %

Question 14: There are two drums, each containing a mixture of paints A and B. In drum 1, A and B are in the ratio 18 : 7. The mixtures from drums 1 and 2 are mixed in the ratio 3 : 4 and in this final mixture, A and B are in the ratio 13 : 7. In drum 2, then A and B were in the ratio

a) 251 : 163

b) 239 : 161

c) 220 : 149

d) 229 : 141

14) Answer (B)

View Video Solution

Solution:

It is given that in drum 1, A and B are in the ratio 18 : 7.

Let us assume that in drum 2, A and B are in the ratio x : 1.

It is given that drums 1 and 2 are mixed in the ratio 3 : 4 and in this final mixture, A and B are in the ratio 13 : 7.

By equating concentration of A

$\Rightarrow$ $\dfrac{3*\dfrac{18}{18+7}+4*\dfrac{x}{x+1}}{3+4} = \dfrac{13}{13+7}$

$\Rightarrow$ $\dfrac{54}{25}+\dfrac{4x}{x+1} = \dfrac{91}{20}$

$\Rightarrow$ $\dfrac{4x}{x+1} = \dfrac{239}{100}$

$\Rightarrow$ $x = \dfrac{239}{161}$

Therefore, we can say that in drum 2, A and B are in the ratio $\dfrac{239}{161}$ : 1 or 239 : 161.

Question 15: The average of 30 integers is 5. Among these 30 integers, there are exactly 20 which do not exceed 5. What is the highest possible value of the average of these 20 integers?

a) 3.5

b) 5

c) 4.5

d) 4

15) Answer (C)

View Video Solution

Solution:

It is given that the average of the 30 integers = 5

Sum of the 30 integers = 30*5=150

There are exactly 20 integers whose value is less than 5.

To maximise the average of the 20 integers, we have to assign minimum value to each of the remaining 10 integers

So the sum of 10 integers = 10*6=60

The sum of the 20 integers = 150-60= 90

Average of 20 integers = $\ \frac{\ 90}{20}$ = 4.5

Question 16: A chemist mixes two liquids 1 and 2. One litre of liquid 1 weighs 1 kg and one litre of liquid 2 weighs 800 gm. If half litre of the mixture weighs 480 gm, then the percentage of liquid 1 in the mixture, in terms of volume, is

a) 80

b) 70

c) 85

d) 75

16) Answer (A)

View Video Solution

Solution:

The weight/volume(g/L) for liquid 1 = 1000

The weight/volume(g/L) for liquid 2 = 800

The weight/volume(g/L) of the mixture = 480/(1/2) = 960

Using alligation the ratio of liquid 1 and liquid 2 in the mixture = (960-800)/(1000-960) = 160/40 = 4:1

Hence the percentage of liquid 1 in the mixture = 4*100/(4+1)=80

Question 17: Two alcohol solutions, A and B, are mixed in the proportion 1:3 by volume. The volume of the mixture is then doubled by adding solution A such that the resulting mixture has 72% alcohol. If solution A has 60% alcohol, then the percentage of alcohol in solution B is

a) 90%

b) 94%

c) 92%

d) 89%

17) Answer (C)

View Video Solution

Solution:

Initially let’s consider A and B as one component

The volume of the mixture is doubled by adding A(60% alcohol) i.e they are mixed in 1:1 ratio and the resultant mixture has 72% alcohol.

Let the percentage of alcohol in component 1 be ‘x’.

Using allegations , $\frac{\left(72-60\right)}{x-72}=\frac{1}{1}$ => x= 84

Percentage of alcohol in A = 60% => Let’s percentage of alcohol in B = x%

The resultant mixture has 84% alcohol. ratio = 1:3

Using allegations , $\frac{\left(x-84\right)}{84-60}=\frac{1}{3}$

=> x= 92%