CAT Time and Work Questions [Most Important]

Time and Work questions are very important in the Arithmetic concept of the CAT Quants section. These questions are not very tough; make sure you are aware of all the Important Formulas in CAT Time and Work. You can also check out these CAT Time and Work questions from the CAT Previous year papers. Practice a good number of questions in CAT Time and Work so that you can easily answer these questions in the exam. This post will look into some important Time and Work Questions for CAT. These are a good source of practice for CAT 2022 preparation; If you want to practice these questions, you can download these Important Time and Work Questions for CAT (with detailed answers) PDF along with the video solutions below, which is completely Free.

Download Time and Work Questions for CAT

Enroll to CAT Mocks at just Rs. 299

Question 1: Anil can paint a house in 12 days while Barun can paint it in 16 days. Anil, Barun, and Chandu undertake to paint the house for ₹ 24000 and the three of them together complete the painting in 6 days. If Chandu is paid in proportion to the work done by him, then the amount in INR received by him is

1) Answer: 3000

View Video Solution

Solution:

Now Anil Paints in 12 Days
Barun paints in 16 Days
Now together Arun , Barun and Chandu painted in 6 Days
Now let total work be W
Now each worked for 6 days
So Anil’s work = 0.5W
Barun’s work = $\frac{6W}{16}=\frac{3W}{8}$
Therefore Charu’s work = $\frac{W}{2}-\frac{3W}{8}=\ \frac{W}{8}$
Therefore proportion of charu =$\frac{24000}{8}=\ 3,000$

Question 2: Mira and Amal walk along a circular track, starting from the same point at the same time. If they walk in the same direction, then in 45 minutes, Amal completes exactly 3 more rounds than Mira. If they walk in opposite directions, then they meet for the first time exactly after 3 minutes. The number of rounds Mira walks in one hour is

2) Answer: 8

View Video Solution

Solution:

Considering the distance travelled by Mira in one minute = M,

The distance traveled by Amal in one minute = A.

Given if they walk in the opposite direction it takes 3 minutes for both of them to meet. Hence 3*(A+M) = C. (1)

C is the circumference of the circle.

Similarly, it is mentioned that if both of them walk in the same direction Amal completes 3 more rounds than Mira :

Hence 45*(A-M) = 3C. (2)

Multiplying (1)*15 we have :

45A + 45M = 15C.

45A – 45M = 3C.

Adding the two we have A = $\frac{18C}{90}$

Subtracting the two M = $\frac{12C}{90}$

Since Mira travels $\frac{12C}{90}$ in one minute, in one hour she travels :$\frac{12C}{90}\cdot60\ =\ 8C$

Hence a total of 8 rounds.

Alternatively,

Let the length of track be L
and velocity of Mira be a and Amal be b
Now when they meet after 45 minutes Amal completes 3 more rounds than Mira
so we can say they met for the 3rd time moving in the same direction
so we can say they met for the first time after 15 minutes
So we know Time to meet = Relative distance /Relative velocity
so we get $\frac{15}{60}=\frac{L}{a-b}$     (1)
Now When they move in opposite direction
They meet after 3 minutes
so we get $\frac{3}{60}=\frac{L}{a+b}$    (2)
Dividing (1) and (2)
we get $\frac{\left(a+b\right)}{\left(a-b\right)}=5$
or 4a =6b
or a = 3b/2
Now substituting in (1)
we get :
$\frac{L}{b}\times\ 2=\ \frac{15}{60}$
so $\frac{L}{b}\ =\frac{1}{8}$
So we can say 1 round is covered in $\frac{1}{8}$ hours
so in 1-hour total rounds covered = 8.

Question 3: One day, Rahul started a work at 9 AM and Gautam joined him two hours later. They then worked together and completed the work at 5 PM the same day. If both had started at 9 AM and worked together, the work would have been completed 30 minutes earlier. Working alone, the time Rahul would have taken, in hours, to complete the work is

a) 11.5

b) 10

c) 12.5

d) 12

3) Answer (B)

View Video Solution

Solution:

Let Rahul work at a units/hr and Gautam at b units/hour
Now as per the condition :
8a+6b =7.5a+7.5b
so we get 0.5a=1.5b
or a=3b
Therefore total work = 8a +6b = 8a +2a =10a
Now Rahul alone takes 10a/10 = 10 hours.

Question 4: Two pipes A and B are attached to an empty water tank. Pipe A fills the tank while pipe B drains it. If pipe A is opened at 2 pm and pipe B is opened at 3 pm, then the tank becomes full at 10 pm. Instead, if pipe A is opened at 2 pm and pipe B is opened at 4 pm, then the tank becomes full at 6 pm. If pipe B is not opened at all, then the time, in minutes, taken to fill the tank is

a) 144

b) 140

c) 264

d) 120

4) Answer (A)

View Video Solution

Solution:

Let A fill the tank at x liters/hour and B drain it at y liters/hour
Now as per Condition 1 :
We get Volume filled till 10pm = 8x-7y       (1) .
Here A operates for 8 hours and B operates for 7 hours .
As per condition 2
We get Volume filled till 6pm = 4x-2y        (2)
Here A operates for 4 hours and B operates for 2 hours .
Now equating (1) and (2)
we get 8x-7y =4x-2y
so we get 4x =5y
y =4x/5
So volume of tank = $8x-7\times\ \frac{4x}{5}=\frac{12x}{5}$
So time taken by A alone to fill the tank = $\frac{\frac{12x}{5}}{x}=\frac{12}{5}hrs\ $
= 144 minutes

Question 5: Anil can paint a house in 60 days while Bimal can paint it in 84 days. Anil starts painting and after 10 days, Bimal and Charu join him. Together, they complete the painting in 14 more days. If they are paid a total of ₹ 21000 for the job, then the share of Charu, in INR, proportionate to the work done by him, is

a) 9000

b) 9200

c) 9100

d) 9150

5) Answer (C)

View Video Solution

Solution:

Let Entire work be W
Now Anil worked for 24 days
Bimal worked for 14 days and Charu worked for 14 days .
Now Anil Completes W in 60 days
so in 24 days he completed 0.4W
Bimal completes W in 84 Days
So in 14 Days Bimal completes = $\frac{W}{6}$
Therefore work done by charu = $W-\frac{W}{6}-\frac{4W}{10}$= $\frac{26W}{10}$=$\frac{13W}{30}$
Therefore proportion of Charu = $\frac{13}{30}\times\ 21000$=9100

Checkout: CAT Free Practice Questions and Videos

Question 6: Amar, Akbar and Anthony are working on a project. Working together Amar and Akbar can complete the project in 1 year, Akbar and Anthony can complete in 16 months, Anthony and Amar can complete in 2 years. If the person who is neither the fastest nor the slowest works alone, the time in months he will take to complete the project is

6) Answer: 32

View Video Solution

Solution:

Let the total work be 48 units. Let Amar do ‘m’ work, Akbar do ‘k’ work, and Anthony do ‘n’ units of work in a month.

Amar and Akbar complete the project in 12 months. Hence, in a month they do $\frac{48}{12}$=4 units of work.

m+k = 4.

Similarly, k+n = 3, and m+n = 2.

Solving the three equations, we get $m=\frac{3}{2},\ k=\frac{5}{2},\ n=\frac{1}{2}$.

Here, Amar works neither the fastest not the slowest, and he does 1.5 units of work in a month. Hence, to complete the work, he would take $\frac{48}{1.5}=32$months.

Question 7: Anu, Vinu and Manu can complete a work alone in 15 days, 12 days and 20 days, respectively. Vinu works everyday. Anu works only on alternate days starting from the first day while Manu works only on alternate days starting from the second day. Then, the number of days needed to complete the work is

a) 5

b) 8

c) 6

d) 7

7) Answer (D)

View Video Solution

Solution:

Let the total amount of work be 60 units.

Then Anu, Vinu, and Manu do 4, 5, and 3 units of work per day respectively.

On the 1st day, Anu and Vinu work. Work done on the 1st day = 9 units

On the 2nd day, Manu and Vinu work. Work done on the 2nd day = 8 units

This cycle goes on. And in 6 days, the work completed is 9+8+9+8+9+8 = 51 units.

On the 7th day, again Anu and Vinu work and complete the remaining 9 units of work. Thus, the number of days taken is 7 days.

Question 8: Two circular tracks T1 and T2 of radii 100 m and 20 m, respectively touch at a point A. Starting from A at the same time, Ram and Rahim are walking on track T1 and track T2 at speeds 15 km/hr and 5 km/hr respectively. The number of full rounds that Ram will make before he meets Rahim again for the first time is

a) 5

b) 3

c) 2

d) 4

8) Answer (B)

View Video Solution

Solution:

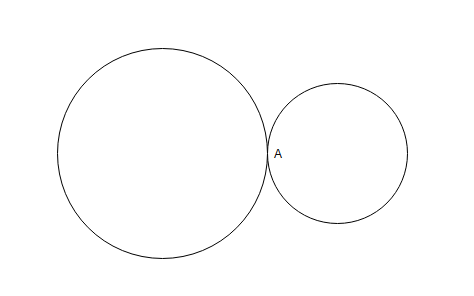
To complete one round Ram takes 100m/15kmph and Rahim takes 20m/5kmph

They meet for the first time after L.C.M of (100m/15kmph , 20m/5kmph) = 100m/5kmph=20m/kmph.

Distance traveled by Ram =20m/kmph * 15kmph =300m.

So, he must have ran 300/100=3 rounds.

Note:

CAT gave both 2 and 3 as correct answers because of the word ‘before‘.

Question 9: A and B are two points on a straight line. Ram runs from A to B while Rahim runs from B to A. After crossing each other. Ram and Rahim reach their destination in one minute and four minutes, respectively. if they start at the same time, then the ratio of Ram’s speed to Rahim’s speed is

a) $\frac{1}{2}$

b) $\sqrt{2}$

c) $2$

d) $2\sqrt{2}$

9) Answer (C)

View Video Solution

Solution:

Let the speed of Ram be v(r) and the speed of Rahim be v(h) respectively. Let them meet after time “t” from the beginning.

Hence Ram will cover v(r)(t) during that time and Rahim will cover v(h)t respectively.

Now after meeting Ram reaches his destination in 1 min i.e. Ram covered v(h)t in 1 minute or v(r)(1)= v(h)(t)

Similarly Rahim reaches his destination in 4 min i.e. Rahim covered v(r)t in 4 minutes or v(h)(4)= v(r)(t)

Dividing both the equations we get $\frac{v\left(r\right)}{4v\left(h\right)}=\frac{v\left(h\right)}{v\left(r\right)}\ or\ \frac{v\left(r\right)}{v\left(h\right)}=2$ Hence the ratio is 2.

Question 10: John takes twice as much time as Jack to finish a job. Jack and Jim together take one-thirds of the time to finish the job than John takes working alone. Moreover, in order to finish the job, John takes three days more than that taken by three of them working together. In how many days will Jim finish the job working alone?

10) Answer: 4

View Video Solution

Solution:

Let Jack take “t” days to complete the work, then John will take “2t” days to complete the work. So work done by Jack in one day is (1/t) and John is (1/2t) .

Now let Jim take “m” days to complete the work. According to question, $\frac{1}{t}+\frac{1}{m}=\frac{3}{2t}\ or\ \frac{1}{m}=\frac{1}{2t\ }or\ m=2t$ Hence Jim takes “2t” time to complete the work.

Now let the three of them complete the work in “p” days. Hence John takes “p+3” days to complete the work.

$\frac{1}{2t}\left(m+3\right)=\left(\frac{4}{2t}\right)m$

$\frac{1}{2t}\left(m+3\right)=\left(\frac{4}{2t}\right)m$

or m=1. Hence JIm will take (1+3)=4 days to complete the work. Similarly John will also take 4 days to complete the work