Average Questions for SSC-CHSL Set-2 PDF
Download SSC CHSL Average Questions with answers Set-2 PDF based on previous papers very useful for SSC CHSL Exams. Top-15 Very Important Questions for SSC Exam
Download Average Questions Set-2 PDF
Get 200 SSC mocks for just Rs. 249. Enroll here
Take a free mock test for SSC CHSL
Download SSC CHSL Previous Papers
More SSC CHSL Important Questions and Answers PDF
Question 1: The average of odd numbers up to 100 is
a) 50.5
b) 50
c) 49.5
d) 49
Instructions
Directions: The pie chart given below show the spending of a family on various heads during a month. Study the graph and answer the questions.

Question 2: If the total income of the family is Rs. 25,000, then the amount spent on Rent and Food together is
a) Rs. 17,250
b) Rs. 14,750
c) Rs. 11,250
d) Rs. 8,500
Question 3: The average of three consecutive odd numbers is 12 more than one-third of the first of these numbers. What is the last of the three numbers?
a) 15
b) 17
c) 19
d) Data inadequate
Instructions
Directions: Population of the five adjacent areas of a town, in the year of 2020, are represented in the following Pie-chart. The ratio of the numbers of males to that of females in these areas are stated in the table below. The total of the population in all the five areas is 72 lakh. Study the Pie-chart and the table and then answer the questions.
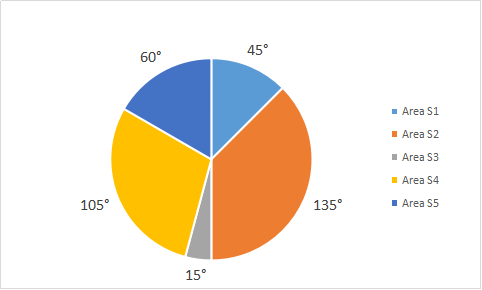
The ratio of number of males(M) to females(F)
Question 4: The average of female population in all the five areas is lower than the female population in each of the areas
a) S1 and S2
b) S2 and S5
c) S2 and S4
d) S4 and S5
Question 5: The average of the first nine integral multiples of 3 is
a) 12
b) 15
c) 18
d) 21
SSC CHSL Study Material (FREE Tests)
Question 6: The average of 6 consecutive natural numbers is K. If the next two natural numbers are also included, how much more than K will the average of these 8 numbers be?
a) 3
b) 1
c) 2
d) 1.8
Question 7: What is the Arithmetic mean of the first ‘n’ natural numbers ?
a) $\frac{n+1}{3}$
b) $\frac{n+1}{2}$
c) $\frac{n+1}{4}$
d) 2(n + 1)
Question 8: Out of four numbers the average of the first three is 16 and that of the last three is 15. If the last number is 20 then the first number is
a) 23
b) 25
c) 28
d) 21
Question 9: The average of 7, 11, 15, x, 14, 21, 25 is 15, then the value of x is
a) 13.3
b) 12
c) 3
d) 14.5
Question 10: The average marks obtained by a student in 6 subjects is 88. On subsequent verification it was found that the marks obtained by him in a subject was wrongly copied as 86 instead of 68. The correct average of the marks obtained by him is
a) 87
b) 85
c) 84
d) 86
Instructions
Given here is a multiple bar diagram of the scores of four players in two innings. Study the diagram and answer the questions:
Question 11: The average runs in two innings of the player who has scored minimum in the second innings are :
a) 30
b) 60
c) 50
d) 40
Question 12: The average marks obtained by 40 students of a class is 86. If the 5 highest marks are removed, the average reduces by one mark. The average marks of the top 5 students is
a) 92
b) 96
c) 93
d) 97
Question 13: The average salary, per head, of all the workers of an institution is 60. The average salary of 12 officers is = 400; the average salary, per head, of the rest is 56. The total number of workers in the institution is
a) 1030
b) 1035
c) 1020
d) 1032
Question 14: The average of 50 numbers is 38. If two numbers, namely 45 and 55 are discarded, the average of the remaining numbers is
a) 37.5
b) 37.9
c) 36.5
d) 37.0
Question 15: The average of 20 numbers is 15 and the average of first five is 12. The average of the rest is
a) 16
b) 15
c) 14
d) 13
Answers & Solutions:
1) Answer (B)
Require sum of 1+3+5+7+9….99
Applying formula for summation of n digits with a as first digit and d is the difference
sum = $\frac{n}{2} (2a + (n-1) d)$
or this formula can be reduced to $\frac{n}{2} \frac{a + l}{2} $hence for calculating avg. it will be
$\frac{a + l}{2}$ (where $l$ is last term)
so $\frac{1 + 99}{2}$ = 50
2) Answer (B)
Total share percentage on food and rent = 45+14 = 59%
Hence price will be = $25000 \times {59}{100} = 14750$
3) Answer (C)
Let’s say numbers are $a, a+2, a+4$
So avg. will be $\frac{(a+a+2+a+4)}{3} = \frac{a}{3} +12$
Or a = 15
So numbers will be 15, 17, 19
4) Answer (A)
5) Answer (B)
As we know average of numbers which are in A.P. is = $\frac{a+l}{2}$ (where a is first term and l is last term)
Here a=3
and l= 27
Hence average will be 15
6) Answer (B)
Let the 6 consecutive numbers be a-3,a-2,a-1,a,a+1,a+2
average = $\frac{SumofElements}{NumberofElements}$
It is given that average of 6 consecutive numbers be k and hence
k = $\frac{a-3+a-2+a-1+a+a+1+a+2}{6}$ = $\frac{6a-3}{6}$ = a – $\frac{1}{2}$
now next two numbers (a+3, a+4) are also added
Sum of 8 numbers = a-3+a-2+a-1+a+a+1+a+2+a+3+a+4 = 8a +4
average of 8 numbers = $\frac{8a+4}{8}$ = a + $\frac{1}{2}$ = k + 1
so average of 8 numbers is more than average of 6 numbers by = k+1 – K = 1
7) Answer (B)
Arithmetic Mean = $\frac{Sumof Elements}{NumberofElements}$
Sum of first n natural numbers = $\frac{n(n+1)}{2}$
Arithmetic Mean of first n natural numbers = $\frac{n(n+1)}{2\times n}$ = $\frac{n+1}{2}$
8) Answer (A)
let the four numbers be a,b,c,d
Using formula average = $\frac{SumofElements}{NumberofElements}$
Now, the average of first 3 numbers = 16
=> Sum of first 3 numbers=a+b+c = 16 × 3 = 48………. (1)
Also, average of last three numbers = 15
=> Sum of last three numbers = b+c+d = 15 × 3 = 45……(2)
Subtracting equation (2) from (1)
=> a – d = 3
Since, d = 20
=> a – 20 = 3
=> a = 23
9) Answer (B)
we know that average =$\frac {sum of elements}{numberof elements} $
Number of elements =7
Sum of elements = 7+11+15+14+21+25+x = 93+x
=> Average = $\frac {93+x}{7} $
=> 15 = $\frac {93+x}{7} $
=> x = 12
10) Answer (B)
Average = $\frac{Sum of Elements}{Number of Elements}$
Number of subjects = 6
wrong average = 88
sum of marks calculated wrongly in all subjects = 88 x 6 = 528
Correct Marks = 528 – 86 + 68 = 510
Correct Average of marks = $\frac{510}{6}$ = 85
11) Answer (D)
In 2nd inning Cheteswar Pujara has scored minimum ,
runs in 1st innings = 70
runs in 2nd innings = 10
Average = $\frac{SumofElements}{NumberofElements}$
average runs = $\frac{70+10}{2}$ = 40
12) Answer (C)
Average = $\frac{SumofElements}{NumberofElements}$
Given that average marks of 40 students in a class = 86
Hence total marks of 40 students = 40 x 86 = 3440
Now when the top 5 highest marks are removed than the average reduces by 1 and hence it become = 86-1 = 85
and number of students now becomes = 40-5 = 35
So total of remaining students = 35 x 85 = 2975
So total marks of top 5 students = 3440 – 2975 = 465
average of 5 students = $\frac{465}{5}$ = 93
13) Answer (D)
Let the total number of members in the institution be z
average = $\frac{SumofElements}{NumberofElements}$
Average salary of institution = Rs 60
total salary of Institution =Rs 60z
Given that out of z persons , there are 12 officers and there average salary is = Rs 400
and so total salary of 12 officers = 12 x 400 =Rs 4800
So total salary of other (z-12) members =Rs ( 60z – 4800 )…………..(1)
It is given that average salary of (z-12) persons = Rs 56
and hence from here the total salary of (z-12) people = Rs 56(z-12)……….(2)
Equation 1 and 2 are equal
60z – 4800 = 56z – 672
4z = 4128
z = 1032
14) Answer (A)
Average = $\frac{Sum of Elements}{Number of Elements}$
Given that Initially Number of Elements = 50
Initial Average = 38
Sum of Elements = 50 x 38 = 1900
Now as two numbers are discarded, hence number of elements left = 48
Sum of elements after discarding numbers = 1900 – 55 – 45 = 1800
Hence New Average = $\frac{1800}{48}$ = 37.5
15) Answer (A)
Given that average of 20 numbers = 15
using average = $\frac{Sum}{Numberof Elements}$
Sum of all numbers = 20 x 15 = 300
Average of first five numbers = 12
So sum of first five numbers = 12×5 = 60
Sum of numbers left = 300 – 60 = 240
Number of numbers left = 20 – 5 = 15
So average of left numbers = $\frac{240}{15}$ = 16
DOWNLOAD APP TO ACESSES DIRECTLY ON MOBILE
We hope this Average Questions for SSC CHSL Exam preparation is so helpful to you.







