Area Questions for CAT
Download important CAT Area Problems with Solutions PDF based on previously asked questions in CAT exam. Practice Area Problems with Solutions for CAT exam.
Download Area Questions for CAT
Download CAT Quant Questions PDF
Question 1: There are two concentric circles such that the area of the outer circle is four times the area of the inner circle. Let A, B and C be three distinct points on the perimeter of the outer circle such that AB and AC are tangents to the inner circle. If the area of the outer circle is 12 square centimeters then the area (in square centimeters) of the triangle ABC would be
a) $\pi\sqrt{12}$
b) $9/\pi$
c) $9\sqrt3/\pi$
d) $6\sqrt3/\pi$
Question 2: In the figure below, ABCDEF is a regular hexagon and $\angle{AOF}$ = 90° . FO is parallel to ED. What is the ratio of the area of the triangle AOF to that of the hexagon ABCDEF?
a) 1/12
b) 1/6
c) 1/24
d) 1/18
Instructions
A punching machine is used to punch a circular hole of diameter two Units from a square sheet of aluminium of width 2 units, as shown below. The hole is punched such that the circular hole touches one corner P of the square sheet and the diameter of the hole originating at P is in line with a diagonal of the square:
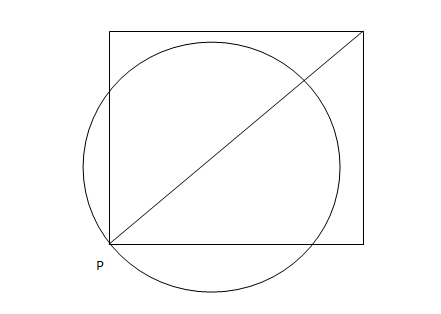
Question 3: Find the area of the part of the circle (round punch) falling outside the square sheet.
a) $\pi$ /4
b) ($\pi$ -1)/2
c) ($\pi$ -1)/4
d) ($\pi$ -2)/2
e) ($\pi$ -2)/4
Question 4: Two identical circles intersect so that their centres, and the points at which they intersect, form a square of side 1 cm. The area in sq. cm of the portion that is common to the two circles is
a) $\pi$/4
b) $\pi$/2-1
c) $\pi$/5
d) $\sqrt\pi-1$
Question 5: In the given diagram, ABCD is a rectangle with AE = EF = FB. What is the ratio of the areas of CEF and that of the rectangle?
a) $\frac{1}{6}$
b) $\frac{1}{8}$
c) $\frac{1}{9}$
d) None of these
Question 6: The area of the triangle whose vertices are (a,a), (a + 1, a + 1) and (a + 2, a) is
[CAT 2002]
a) $a^3$
b) $1$
c) $2a$
d) $2^{1/2}$
Question 7: A circle is inscribed in a given square and another circle is circumscribed about the square. What is the ratio of the area of the inscribed circle to that of the circumscribed circle?
a) 2 : 3
b) 3 : 4
c) 1 : 4
d) 1 : 2
Question 8: The sum of the areas of two circles, which touch each other externally, is $153\pi$. If the sum of their radii is 15, find the ratio of the larger to the smaller radius.
a) 4
b) 2
c) 3
d) None of these
Question 9: In the adjoining figure, points A, B, C and D lie on the circle. AD = 24 and BC = 12. What is the ratio of the area of CBE to that of ADE?
a) 1 : 4
b) 1 : 2
c) 1 : 3
d) Data insufficient
Question 10: Four identical coins are placed in a square. For each coin the ratio of area to circumference is same as the ratio of circumference to area. Then find the area of the square that is not covered by the coins.
a) 16(π – 1)
b) 16(8 – π)
c) 16(4 – π)
d) 16 $(4- \frac{\pi}{2})$
Take a free CAT online mock test
Answers & Solutions:
1) Answer (C)
Let R ,r be radius of big and small circles respectively. We know that R=2r.
And since area = 12 ;
$R^2 = \frac{12}{\pi}$.
By pythagoras theorem in the small triangle with side ‘x’ we have x = 3 / $\sqrt{\pi}$.
This triangle is a 30-60-90 right triangle. => Triangle ABC is an equilateral triangle.
So side of triangle ABC = 2x = 6 / $\sqrt{\pi}$.
Also Angle OAB = 30 (as side opposite to the angle is half of the hypotenuse ) .
Hence Angle CAB = 60. Hence required triangle is an equilateral triangle. So area = $\sqrt{3}$ * (2x)$^2$ / 4 . Substituting we get . Area = $9\sqrt3/\pi$.
2) Answer (A)
When the hexagon is divided into number of similar triangle AOF we get 12 such triangles . Hence required ratio of area is 1/12.
3) Answer (D)
The area of triangle ABC is 1/2 * $\sqrt2$ * $\sqrt2$ = 1
Area of semi-circle ABC = $\pi/2$
So, area of circle outside the square = $\pi/2$ – 1 = ($\pi$ -2)/2
4) Answer (B)
We know that quad pmqn is a square of side 1.
Area of the sector p-mqn is $\frac{45}{360}* \pi *1*1$ = $\frac{\pi }{4}$.
Area of square = 1*1 = 1
Area of common portion = 2 * Area of sector – Area of square
= 2 * $\frac{\pi }{4}$ – 1 = $\frac{\pi }{2}$ – 1
5) Answer (A)
Area of triangle CEF = 1/2 * length of rectangle/3 * breadth of rectangle = Area of rectangle/6
So, required ratio = 1:6
CAT Online Most Trusted Courses
6) Answer (B)
The length of three sides is $\sqrt 2, \sqrt 2$ and $2$.
This is a right-angled triangle.
Hence, it’s area equals $1/2 * \sqrt 2 * \sqrt 2 = 1$
So, the correct answer is b)
7) Answer (D)
As we know that area of the circle is directly proportional to the square of its radius.
Hence $\frac{A_{ic}}{A_{cc}} = \frac{\frac{x^2}{4}}{\frac{x^2}{2}}$
Where $x$ is side of square (say), ic is inscribed circle with radius $\frac{x}{2}$, cc is circumscribed circle with radius $\frac{x}{\sqrt{2}}$
So ratio will be 1:2
8) Answer (A)
Given:
$\pi((r_1)^2 + (r_2)^2) = 153\pi$
So
$(r_1)^2 + (r_2)^2 = 153$
Or $((r_1) + (r_2))^2 – 2(r_1)(r_2) = 153$
Or $(r_1)(r_2) = 36$ and $(r_1) + (r_2) = 15$
$r_1 = 12$
$r_2 = 3$
Ratio = 4
9) Answer (A)
As we know angles of same sectors are equal
Hence angle B and angle D will be equal. Angle BCE and angle EAD will be equal.
So triangles BCE and EAD will be similar triangles with sides ratio as 12:24 or 1:2.
Area will be in ratio of 1:4.
10) Answer (C)
$\frac{(\pi r^2)}{2 \pi r}$ = $\frac{2 \pi r}{ \pi r^2}$
So r = 2
Hence required area = (Area of square) – (Area of 4 circles)
= $(8^2) – (4 \pi (2^2))$ (As side of square will be 4*2 = 8)
= $16 (4- \pi)$
Download CAT Previous Papers PDF
Download Free CAT Preparation App
We hope this CAT Area Problems with Solutions PDF will be helpful to you.
