Advance Maths Questions for SSC CGL PDF
Download SSC CGL Advance Maths Questions PDF based on previous papers very useful for SSC CGL Exams. Top-15 Very Important Maths Questions for SSC CGL Exam.
Download Advance Maths Questions for SSC CGL PDF
Get 200 SSC mocks for just Rs. 249. Enroll here
Question 1: A car is travelling on a straight road leading to a tower. From a point at a distance of 500 m from the tower, as seen by the driver, the angle of elevation of the top of the tower is 30°. After driving towards the tower for 10 seconds, the angle of elevation of the top of the tower as seen by the driver is found to be 60°. Then the speed of the car is
a) 135 km/hr.
b) 110 km/hr.
c) 120 km/hr.
d) 90 km/hr.
Question 2: The value of $\frac{sin39^{\circ}}{cos51^{\circ}}$ + $2 tan11^{\circ} tan31^{\circ} tan45^{\circ} tan59^{\circ} tan79^{\circ}$ – $3(sin^{2}21^{\circ} + sin^{2}69^{\circ})$ is
a) 1
b) 2
c) -1
d) 0
Question 3: Find equation of the perpendicular to segment joining the points A(0,4) and B(-5,9) and passing through the point P. Point P divides segment AB in the ratio 2:3.
a) x – y = 8
b) x – y = -8
c) x + y = -8
d) x + y = 8
Question 4: In a class, there are 40 students. Some of them passed the examination and others failed. Raman’s rank among the student who have passed is 13 th from top and 17 th from bottom. How many students have failed?
a) 11
b) 10
c) 9
d) Cannot be determined
Question 5: A number is increased by 30%, then decreased by 30%, then further decreased by 30%. What is the net increase/decrease percent in the number(correct to the nearest integer)?
a) 36% decrease
b) 36% increase
c) 40% increase
d) 40% decrease
Take a free mock test for SSC CGL
Download SSC CGL Previous Papers PDF
18000+ Questions – Free SSC Study Material
Question 6: A cuboid has dimensions $8 cm \times 10 cm \times 12 cm$. It is cut into small cubes of side $2 cm$. What is the percentage increase in the total surface area?
a) 286.2
b) 314.32
c) 250.64
d) 386.5
Question 7: A scooter is sold at three successive discounts of 10%, 5% and 2%. If the marked price of the scooter is Rs.18,000, find its net selling price.
a) Rs.15028.20
b) Rs.15082.00
c) Rs.15082.20
d) Rs.15080.00
Question 8: The average marks obtained by 150 students in an examination is 40. If the average marks of passed students is 60 and that of the failed students is 20, then what is the number of students who passed the examination?
a) 25
b) 50
c) 75
d) 100
Question 9: A solution of milk and water contains milk and water in the ratio of 3 : 2. Another solution of milk and water contains milk and water in the ratio of 2 : 1. 40 liters of the first solution is mixed with 30 liter of the second solution. The ratio of milk and water in the resultant solution is:
a) 22:13
b) 13:22
c) 6:5
d) 5:6
Question 10: Teena, Reena and Sheena start a business with investment of respectively ₹ 24000, ₹ 28000 and ₹ 20000. Teena invests for 8 months, Reena invest for 10 months and Sheena invests for one year. If the total profit at the end of year is ₹ 25810, then what is the share of Teena?
a) ₹6960
b) ₹10150
c) ₹7940
d) ₹8700
More SSC CGL Important Questions and Answers PDF
Question 11: How many job applicants had applied if the ratio of selected to unselected was 19:17. If 1,200 less had applied and 800 less selected, then the ratio of selected to unselected would have been 1:1.
a) 6000
b) 7200
c) 8400
d) 4800
Question 12: A train takes 1 minute to cross a stationary pole. How much time (in seconds) will it take to cross a bridge whose length is twice that ofthe train?
a) 120
b) 90
c) 150
d) 180
Question 13: Pipe P can fill a tank alone in 7 hours. Pipe Q can fill the same tank alone in 13 hours. In how much time can they togetherfill the tank?
a) 3 hours 18 minutes
b) 3 hours 45 minutes
c) 4 hours 12 minutes
d) 4 hours 33 minutes
Question 14: Two places P and Q are 162 km apart. A train leaves P for Q and simultaneously another train leaves Q for P. They meet at the end of 6 hours. If the former train travels 8km/hour faster then the other, then speed of train from Qis
a) 9 $\frac{1}{2}$ km/hr
b) 10 $\frac{5}{6}$ km/hr
c) 12 $\frac{5}{6}$ km/hr
d) 9 $\frac{1}{2}$ km/hr
e) 8 $\frac{1}{2}$ km/hr
Question 15: ABCD is a square. Draw an equilateral triangle PBC on side BC considering BC is a base and an equilateral triangle QAC on digonal AC considering AC is a base. Find the value of $\ \frac{Area \ of \ \triangle PBC}{Area \ of \ \triangle QAC}$
a) $\frac{1}{2}$
b) 1
c) $\frac{1}{3}$
d) $\frac{1}{4}$
SSC CGL Previous Papers Download PDF
Answers & Solutions:
1) Answer (C)
BC = 500 m
Let CD be $x$ => BD = $500 – x$
From $\triangle$ABC
=> $tan 30 = \frac{AB}{BC}$
=> $\frac{1}{\sqrt{3}} = \frac{AB}{500}$
=> $AB = \frac{500}{\sqrt{3}}$ m
Now, from $\triangle$ABD
=> $tan 60 = \frac{AB}{BD}$
=> $\sqrt{3} = \frac{\frac{500}{\sqrt{3}}}{500 – x}$
=> $3 (500 – x) = 500$
=> $3x = 1000$
$\therefore x = \frac{1000}{3}$ metre = $\frac{1}{3}$ km
Also, speed of car = $\frac{distance}{time}$
= $\frac{\frac{1}{3}}{\frac{10}{60 * 60}}$ km/hr
= 120 km/hr
2) Answer (D)
Expression : $\frac{sin39^{\circ}}{cos51^{\circ}}$ + $2 tan11^{\circ} tan31^{\circ} tan45^{\circ} tan59^{\circ} tan79^{\circ}$ – $3(sin^{2}21^{\circ} + sin^{2}69^{\circ})$
= $\frac{sin 39^{\circ}}{cos (90^{\circ} – 39^{\circ})}$ + $2 \times tan 11^{\circ} \times tan 31^{\circ}$ $\times 1 \times tan (90^{\circ} – 31^{\circ}) \times tan (90^{\circ} – 11^{\circ})$ – $3 [sin^2 21^{\circ} + cos^2 (90^{\circ} – 21^{\circ})]$
= $\frac{sin 39^{\circ}}{sin 39^{\circ}}$ + $2 \times tan 11^{\circ} \times cot 11^{\circ} \times tan 31^{\circ} \times cot 31^{\circ}$ – $3(sin^2 21^{\circ} + cos^2 21^{\circ})$
= $1 + 2 – 3 = 0$
3) Answer (B)
Using section formula, the coordinates of point that divides line joining A = $(x_1 , y_1)$ and B = $(x_2 , y_2)$ in the ratio a : b
= $(\frac{a x_2 + b x_1}{a + b} , \frac{a y_2 + b y_1}{a + b})$
Coordinates of A(0,4) and B(-5,9). Let coordinates of P = (x,y) which divides AB in ratio = 2 : 3
=> $x = \frac{(2 \times -5) + (3 \times 0)}{2 + 3}$
=> $5x = -10$
=> $x = \frac{-10}{5} = -2$
Similarly, $y = \frac{(2 \times 9) + (3 \times 4)}{2 + 3}$
=> $5y = 18 + 12 = 30$
=> $y = \frac{30}{5} = 6$
=> Point P = (-2,6)
Slope of AB = $\frac{9 – 4}{-5 – 0} = \frac{5}{-5} = -1$
Let slope of line perpendicular to AB = $m$
Also, product of slopes of two perpendicular lines is -1
=> $m \times -1 = -1$
=> $m = 1$
Equation of lines having slope $m$ and passing through point P(-2,6) is
=> $(y – 6) = 1(x + 2)$
=> $y – 6 = x + 2$
=> $x – y = -8$
=> Ans – (B)
4) Answer (A)
Total number of students = 40
Among the student who have passed, Raman’s rank from top = 13th
Raman’s rank from bottom = 17th
=> Total students who passed = $(13+17)-1=30-1=29$
$\therefore$ Number of students who have failed = $40-29=11$
=> Ans – (A)
5) Answer (A)
Let the number is 100
First, Increased by 30% = $\frac{130}{100} \times 100 = 130$
Then, decreased by 30% = $\frac{70}{100} \times 130 = 91$
Then further decreased by 30% = $\frac{70}{100} \times 91 = 63.7$
So change = $63.7-100=-36.3$ or $36.3$ % decrease.
$\therefore$ change % = $36$% decrease (nearest integer)
6) Answer (D)
Surface area of cuboid=2(8×12+12×10+8×10)=592 .
Let say it cutted into n number of small cubes.
Then according to question:
$n×2^3=8×12×10$
or, n=120.
So, Total surface area of all cubes
$=120×6×2^2$=2880.
So, percentage increase in Total surface area=((2880-592)/592)×100=386.4%.
D is correct choice.
7) Answer (C)
Marked price = Rs. 18,000
Selling price after first discount of 10% = $18,000-(\frac{10}{100}\times18,000)$
= $18,000-1800=Rs.$ $16,200$
Similarly, selling price after second discount of 5% = $16,200-(\frac{5}{100}\times16,200)$
= $16,200-810=Rs.$ $15,390$
And selling price after third discount of 2% = $15,390-(\frac{2}{100}\times15,390)$
= $15,390-307.8=Rs.$ $15,082.20$
=> Ans – (C)
8) Answer (C)
Let the number of students who passed the examination = $x$
=> Number of students who failed = $(150-x)$
Average marks of 150 students = 40
=> Total marks = $40\times150=6000$
Similarly, total marks scored by passed students = $60x$
According to ques,
=> $60x+20(150-x)=6000$
=> $60x+3000-20x=6000$
=> $40x=6000-3000=3000$
=> $x=\frac{3000}{40}=75$
$\therefore$ The number of students who passed the examination = 75
=> Ans – (C)
9) Answer (A)
Ratio of milk to water in solution 1 is 3:2
Solution 1 contains 40 liters.
Milk content in solution 1 =(3/5)*40
=24 liters
Water content=40-24=16 liters
Ratio of milk to water in solution 2 is 2:1
Solution 2 contains 30 liters.
Milk content in solution 2 =(2/3)*30
=20 liters
Water content=30-20=10 liters
Total milk content=24+20=44 liters
Total water content =16+10=26 liters
Ratio=22:13
10) Answer (A)
Investment of Teena = Rs.24000
Duration of Teena = 8 months
Total investment of Teena = $Rs.24000 \times 8$
Investment of Reena = Rs.28000
Duration of Reena = 10 months
Total investment of Reena = $Rs.28000\times10$
Investment of Sheena = Rs.20000
Duration of Sheena = 12 months
Total investment of Sheena = $Rs.20000\times12$
Ratio of profits = Ratio of investments = $Rs.24000 \times 8 : Rs.28000\times10 : Rs.20000\times12 = 24 : 35 : 30$
Given, Total profit = Rs.25810
Then, Profit of Teena = $\dfrac{24}{89} \times 25810 = Rs.6960$
11) Answer (B)
Let s and u be the no. of candidates selected and unselected respectively.
Total candidates applied = s+u
Condition 1:
Ratio of selected to unselected was 19: 17.
s/u = (19/17)
17s= 19u ——(1)
Condition 2:
If 1200 less had applied and 800 less selected, the ratio of selected to unselected would have been 1 : 1
Total candidates applied = s+u-1200
Selected candidates = s-800
Then, unselected candidates = s+u-1200 – (s-800) = s+u-1200-s+800 = u-400
(s-800)/(u-400) = (1/1)
s-800 = u-400 —-(2)
From (1),
u = (17/19)s
Substitute in (2),
s-800 = (17/19)s -400
s= 3800
u = 3400
s+u = 3800 + 3400 = 7200
The number of applicants is 7200
B is correct choice.
12) Answer (D)
As we know that
Speed = $\frac{distance}{time}$
Given
Let train length = D
Speed = $\frac{D}{60}$
Now
Given that
Bridge length = 2D
Time = $\frac{bridge length+ train }{speed}$
Time = $\frac{2D+ D }{\frac{D}{60}}$
Time = 180
13) Answer (D)
P = 7 hrs
Q =13 hrs
Total work = lcm (7,13)= 91 hrs
P’s effiency = $91\div7$ =13
Q’s effiency = $91\div13$ =7
(P+Q)’s together takes = $Total work\div total efficency$
= $91\div20$
convert 91 hrs into minutes = $91\times 60=5460$
= $5460\div20$
= 273 min
= $273\div60$
=4 hours 33 minutes
14) Answer (A)
Let the speed of the train from Q be X km/hr
Then the speed of the train from P is ( X+8 ) km/hr
They meet each other at M after 6 hours travel
PM + MQ = 162 km
6 ( X + 8 ) + 6X = 162 km
12X + 48 = 162
12X = 162 – 48
12X = 114
X = 114/12
9 (1/2) km/hr
15) Answer (A)
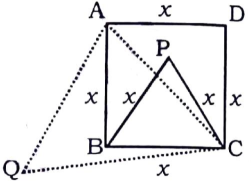
Let side of the square be $x$ cm
=> Side of equilateral $\triangle$ PBC = $x$ cm
In right $\triangle$ ABC,
=> $(AC)^2=(AB)^2+(BC)^2$
=> $(AC)^2=(x)^2+(x)^2=2x^2$
=> $AC=\sqrt2x$
$\therefore$ $\ \frac{ar(\triangle PBC)}{ar(\triangle QAC)}$
= $[\frac{\sqrt3}{4}\times (x)^2]\div[\frac{\sqrt3}{4}\times (\sqrt2x)^2]$
= $\frac{x^2}{2x^2}=\frac{1}{2}$
=> Ans – (A)
Get 200 SSC mocks for just Rs. 249. Enroll here
We hope this Advance Maths Questions for SSC CGL Exams will be highly useful for your preparation.






