Venn Diagram Questions for RRB Group-D PDF
Download Top 15 RRB Group-D Venn Diagram Questions and Answers PDF. RRB Group-D Venn Diagram questions based on asked questions in previous exam papers very important for the Railway Group-D exam.
Download Venn Diagram Questions for RRB Group-D PDF
Download RRB Group-D Previous Papers PDF
Take a RRB Group-D free mock test
Question 1: A school has 100 students. All the students were surveyed for the Shampoo they use among Clinic minus, Shoulders and head, and Moonsilk. All the students in the school admitted to using at least one of these 3 shampoos. 40 students said they use Clinic minus, 30 students said they use Shoulders and head, and 60 students reported to use Moonsilk. If it is known that 10 students use all 3 shampoos, how many students use exactly one of the three shampoos?
a) 60
b) 70
c) 80
d) 90
Question 2: 500 children eat at least one amongst apples, bananas and oranges. 240 eat apples and 190 eat bananas. If the maximum number of children who eat all three fruits can be 50. How many must be eating oranges?
a) 100
b) 120
c) 170
d) 200
Question 3: In a city of 800 families, 500 families do not possess a car and 400 people do not possess a bike. If it is known that 100 families own both car and bike, how many families do not own any vehicle?
a) 325
b) 275
c) 300
d) 225
e) 200
Take a free mock test for RRB Group-D
770 Mocks (cracku Pass) Just Rs.199
Question 4: An electronic shop offers mobiles of Samsung, Nokia and OnePlus. During a given day, 300 customers visited the shop. The number of people who bought phones of only one company is one and a half times greater than the number of people who bought phones of all three companies. For the shopkeeper, the customers who gave the most amount of profit was earned from the people who bought phones of two companies only. The profit from each phone is same. What is the minimum possible value of the number of people who bought phones of two companies ? Assume that all the people who came in the store bought atleast one phone.
a) 1
b) 6
c) 10
d) 15
e) None of the above
Question 5: In a society of 800 people, each person reads at least one type of newspaper between The Hindu, Times of India and Economic Times. 37.5% of the people living in the society are men. Economic Times is read entirely by women, while men who read only the Hindu are three times the number of Men who only read the Times of India (which is a multiple of 50). If 200 people read both the Hindu and Times of India but not Economic Times. How many women read Times of India and The Hindu but not Economic Times?
a) 100
b) 50
c) 150
d) 200
Question 6: In the census of the men of a village was conducted and the following results were obtained : n(not businessmen) = 350, n(businessmen) = 30% of total men. It is also known that married businessmen and single men not doing business combined make 50% of the total male population. Find the maximum number of married men not engaged in business.
a) 120
b) 150
c) 250
d) 100
RRB Group D previous year papers
Question 7: In an examination of 3 subjects physics (P), chemistry (C) and mathematics (M), 50 students passed in all the subjects out of a total of 500. If the ratio of the number of students who passed only in PM, only in PC and only in CM respectively are in the ratio 1:2:3 and the number of students who passed only in P,C and M are in the ratio 5:4:3 respectively, then what is the maximum number of people who passed only in mathematics?
a) 74
b) 222
c) 111
d) 185
Question 8: In a township of 1000 families, 350 own an SUV. Out of those who own an SUV, 50% own a car too. If it is known that 75% of the families of the township owns at least one vehicle, how many families own at most one vehicle?.
Question 9: A survey was conducted in a town to gauge the popularity of 2 detergent powders viz. Sariel and Turf Excel. A total of 800 housewives participated in the survey. It was found that 544 housewives knew about Sariel whereas only 378 housewives knew about Turf Excel. What can be the number of housewives who knew about Sariel alone?
a) 150
b) 425
c) 165
d) 394
Question 10: Raju, an investment banker lived in Goa for few days. On each day, either for lunch or dinner, he tried at most one of the two Portuguese dishes Caldo Verde or Bebinca. If he didn’t eat any of the two dishes on 27 lunches and on 37 dinners but he had one of two dishes 28 times, then find the number of days that Raju spent in Goa.
a) 54 days
b) 82 days
c) 46 days
d) 60 days
RRB Group-D Important Questions (download PDF)
Question 11: A total of 100 employees participated in a survey. The employer asked the employees to vote for the vacation destination that they like. One can choose one or more destination out of 3 choices viz. Dubai, Melbourne, and Paris. Only 30 employees voted for Dubai whereas 70 employees voted for Paris. If it is given that 60 employees voted for Melbourne and none of the employees voted for all three cities, then find out the ratio of the number of employees who voted for exactly one city to the number of employees who voted for more than one city.
a) 2 : 5
b) 3 : 5
c) 2 : 3
d) 3 : 2
Question 12: There are a total of 50 students in a class. All of them like at least one beverage among pepsi, coke and coffee. 5 students like all three beverages whereas the number of students who like both coffee and pepsi is 3 more than the number of students who like both pepsi and coke. If a total of 31 students like more than 1 beverage and the number of students who like both coke and coffee is twice that of the number of students who like both pepsi and coffee, then find out the number of students who like both pepsi and coffee but not coke?
a) 5
b) 6
c) 7
d) 8
Question 13: If A = {$6^{2n} -35n – 1$}, where $n$ = 1,2,3,… and B = {35($n$-1)}, where $n$ = 1,2,3,… then which of the following is true?
a) Every member of A is in B and at least one member of B is not in A
b) Neither every member of A is in B nor every member of B is in A
c) Every member of B is in A.
d) At least one member of A is not in B
Question 14: For two sets A and B, let AΔB denote the set of elements which belong to A or B but not both. If P = {1,2,3,4}, Q = {2,3,5,6,}, R = {1,3,7,8,9}, S = {2,4,9,10}, then the number of elements in (PΔQ)Δ(RΔS) is
Question 15: If among 200 students, 105 like pizza and 134 like burger, then the number of students who like only burger can possibly be
a) 23
b) 26
c) 96
d) 93
General Science Notes for RRB Exams (PDF)
Answers & Solutions:
1) Answer (C)
Let us name the regions as shown in the figure.

a+b+c+d+e+f+10 = 100
=> a+b+c+d+e+f = 90 ————-(1)
a+b+d+10 = 40
a+b+d = 30 ——–(2)
b+c+e+10 = 30
b+c+e = 20 ——–(3)
d+e+f+10 = 60
d+e+f = 50 ———(4)
Adding (2), (3), and (4), we get,
a+2b+c+2d+2e + f = 100 ———-(5)
Subtracting (1) from (5), we get,
b+d+e = 10
=> Number of students who use exactly 2 of the 3 shampoos is 10.
We know that the number of students who use all 3 shampoos = 10.
=> Number of students who use exactly 1 of the 3 shampoos = 100-10-10 =80.
Therefore, option C is the right answer.
2) Answer (C)
Let the number of children who eat only one fruit be o, the number of children who eat two fruits be t and the number of children who eat all three fruits be h.
Then, o+t+h=500
Let us take the number of children who eat oranges as x, then o+2t+3h=240+190+x
Or o+2t+3h=430+x
Using the first equation in the second, we have t+2h+500=430+x
Or t+2h=x-70
Now, it is given that the maximum h can be is 50. This would mean that t would have to be minimized for h to be maximized, i.e. t=0.
So, 0+2*50=x-70
Or x=170.
Option C is the correct answer.
3) Answer (E)
Let us draw the venn diagram.
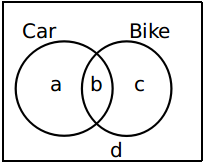
b = 100 (given)
500 families do not own a car
=>c + d = 500……(i)
400 people do not possess a bike
=>a + d = 400……(ii)
Adding (i) and (ii), we get
a + c + 2d = 900……….(iv)
Also, we know that a + b + c + d = 800
or, a + c+ d = 800 – 100 = 700……..(v)
From (iv) and (v), we get
d = 200
So, 200 families do not own any vehicle.
Hence, option E is the correct answer.
4) Answer (B)
Let us draw the venn diagram of the given situation.
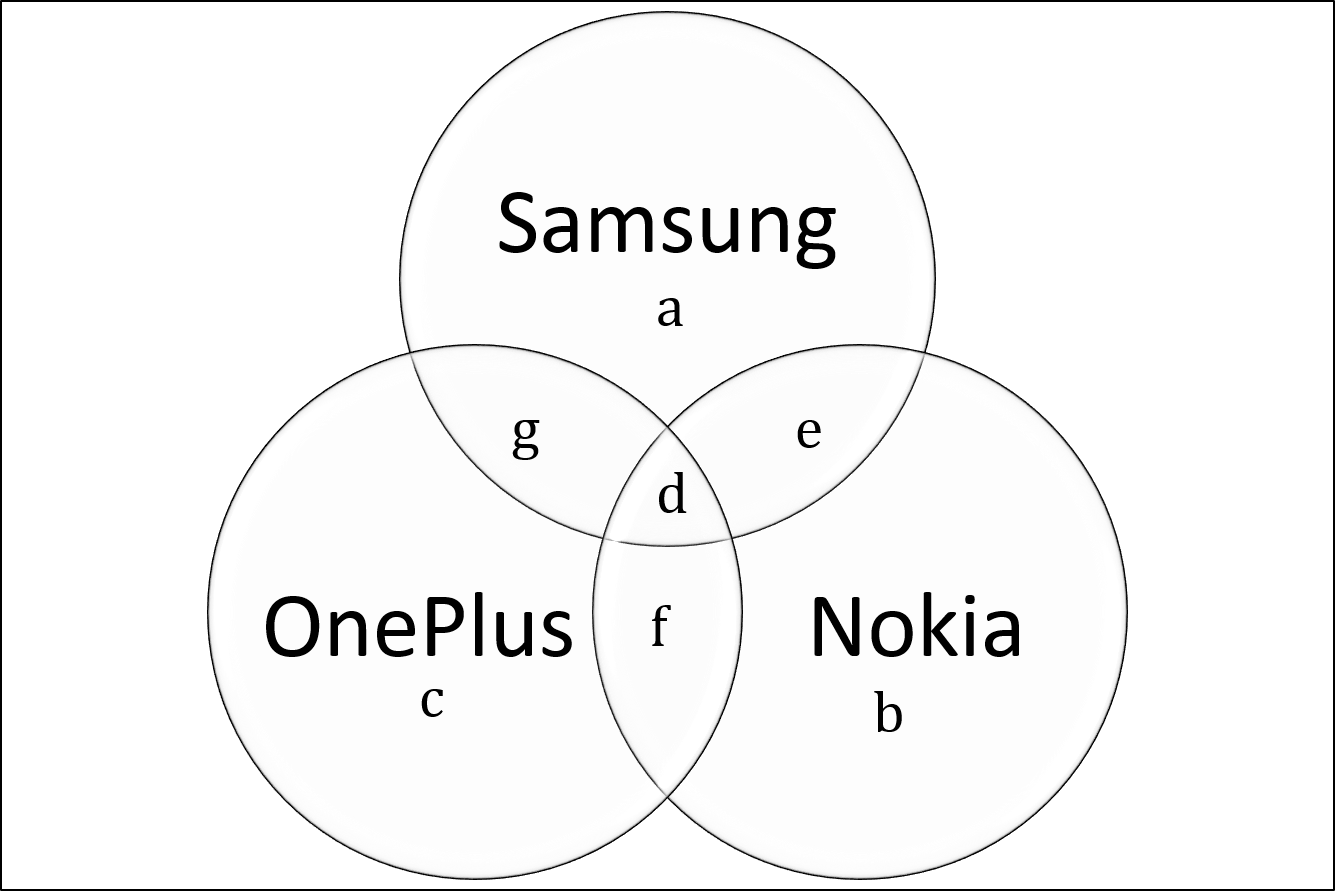
We know that $a+b+c+d+e+f+g = 300$ —–(1)
Also, $a+b+c = (1+ \dfrac{3}{2}) \times d $
$ \Rightarrow a+b+c = \dfrac{5d}{2} $
Let the total number of people who purchased phones from 2 companies ie $e+f+g$ be $x$.
Thus, equation (1) can be written as $d + \dfrac{5d}{2} + x = 300 \Rightarrow \dfrac{7d}{2} + x = 300$ —-(2)
Now, since we need to minimize the value of $x$, we need to maximize the value of $d$.
It should be carefully noted that the value of $d$ should be such that $\dfrac{5d}{2}$ is a natural number.
Thus, $d_{max} = [\dfrac{300}{\frac{7}{2}}] = [\dfrac{300 \times 2}{7}] $
$ \Rightarrow d_{max} = [\dfrac{600}{7}] = 85 $
Since 85 is the maximum value of $d$ possible but it would result in $\dfrac{5d}{2}$ not being a natural number. Thus we take the largest number less than 85 which is a multiple of 2 ie 84.
Putting $d$=84 in equation (2),
$\dfrac{7 \times 84}{2} + x = 300 \Rightarrow x = 300-294 = 6 $
5) Answer (A)
The diagram shows the information given in the question. Since the entire readership of Economic Times (ET) is women, we know that men must be distributed amongst those who read only The Hindu (TH), those who read only the Times of India (TOI) and those who read TH and TOI but not ET.
Total men: 37.5% of 800=300
Taking only TOI and male readers as x. We get only TH and male readers as 3x. It is given that x must be a multiple of 50, so x has to be 50 (if it was 100 there would be more men than the total given.) Since 200 men get distributed between only TH and TOI readers, 100 must be both TH and TOI readers. As the total TH and TOI readers but not ET readers is given as 200, it means the number of women who must read TH and TOI but not ET is 200-100=100.
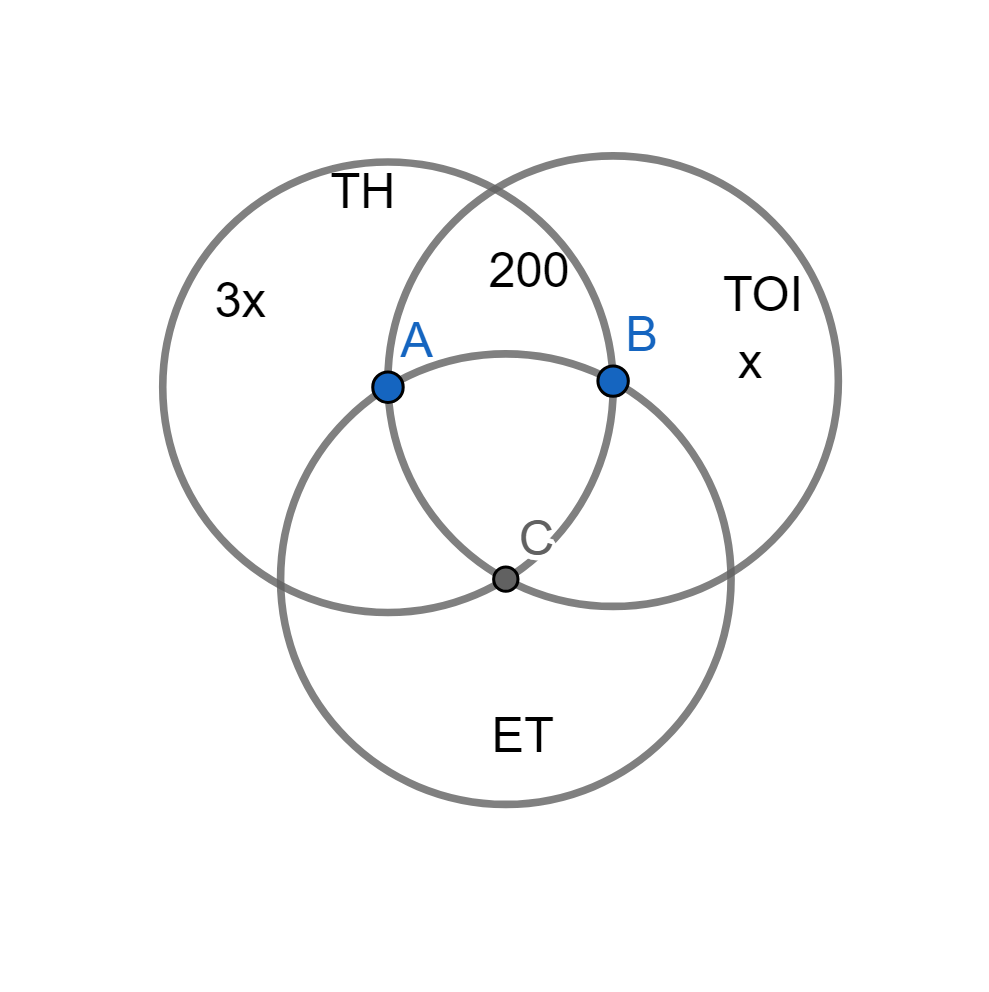
6) Answer (C)
Let us draw the venn diagram of the given situation :

From the information give, we know that
$c+d=350$ — (1)
$a+b=\dfrac{3}{10} \times (a+b+c+d)$ —-(2)
Putting value of equation (1) in equation (2)
$a+b = \dfrac{3}{10} \times (a+b+350)$
$a+b(1- \dfrac{3}{10}) = 105 $
$a+b = \dfrac{105}{\dfrac{7}{10}} $
$a+b= 150$ —–(3)
Thus, total men = 350 + 150 = 500
Also, $b+d = \dfrac{1}{2} \times (a+b+c+d) $
$ \Rightarrow b+d = \dfrac{1}{2} \times 500 $
$ \Rightarrow b+d = 250 $ — (4)
Putting value of $d$ from equation (1) in equation (4),
$ b + 250 – c = 250 $
$ \Rightarrow c – b = 100 $
$ \Rightarrow c = b+100 $
Now, from equation (3) and equation (4), we know
$ b = 150 – a $ and $ b = 250-d $
Thus, the maximum value of $b$ possible is 150 (assuming $a$=0).
We cannot assume $d$=0 because in that case $a+b >150$
Thus, maximum value of $c_{max} = 150+100 = 250$
7) Answer (C)
Let the number of students who passed in PM, PC and CM respectively be $x$,$2x$ and $3x$.
Let the number of students who passed only in P,C,M be $5y$,$4y$ and $3y$ respectively.
Then the venn diagram of the situation can be drawn as :
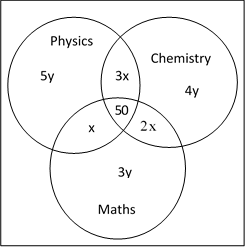
Since we are asked the maximum number of people who passed in mathematics, thus for this situation we need to minimize all the other values.
Thus, for the people who passed in 2 subjects only, we put x=1 to obtain the least value.
Thus, number of people who passed in 2 subjects only = (x+2x+3x) = 6x = 6 people
Thus, the total of people who passed in only 1 subject = 500 – (50+6) = 444 people
Also given, $444 = 5y+4y+3y$
$ \Rightarrow 12y = 444 $
$\Rightarrow y = \dfrac{444}{12} = 37$
Maximum number of people who passed only in maths = 3 x 37 = 111 people
8) Answer: 825
No. of families who owns an SUV = 350
No. of families who owns both SUV and car = 50% of 350 = 175
It is given that 75% of the families own at least one vehicle.
So, 250 families do not own any vehicle.
No. of families who own a vehicle other than a SUV = 750 – 350 = 400
So, no of families who own at most one vehicle
= 250 + (350 – 175) + (750 – 350) = 825
Hence, 825 is the correct answer.
9) Answer (D)
Let ‘$x$’ be the number of housewives who knew about both detergent powders. Let ‘$y$’ be the number of housewives who didn’t know about any of the two brands. We can draw a Venn diagram as shown below:
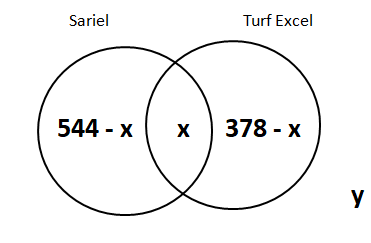
It is given that a total of 800 housewives participated in the survey.
$\Rightarrow$ $544-x+x+378-x+y=800$
$\Rightarrow$ $x = 122+y$
We know that $y \geq 0$, therefore, we can say that $x \geq 122$ … (1)
Also, the number of housewives who knew about Turf excel alone = $378 – x$. Therefore, $378 – x \geq 0$
$\Rightarrow$ $x \leq 378$ … (2)
By combining inequality (1) and (2) we can say that
$\Rightarrow$ $122 \leq x \leq 378$
$\Rightarrow$ $-122 \geq -x \geq -378$
$\Rightarrow$ $544-122 \geq 544-x \geq 544-378$
$\Rightarrow$ $166\leq 544-x \leq 422$
Hence, the number of housewives who knew about Sariel alone = (544 – x) $\epsilon$ [166, 422]
We can see that only 394 lies in that range. Therefore, option D is the correct answer.
10) Answer (C)
Let ‘n’ be the number of days for which Raju stayed in Goa.
Let ‘x’ and ‘y’ be the number of lunches and dinners occasion when Raju had one of the two dishes.
It is given that x + y = 28 … (1)
Also n – x = 27 … (2)
$\Rightarrow$ n – y = 37 … (3)
By equation (2) and (3) we can say that
2n – (x+y) = 27 + 37
$\Rightarrow$ 2n = 64+28
$\Rightarrow$ n = 46
Therefore, we can say that Raju lived in Goa for 46 days. Hence, option C is the correct answer.
11) Answer (C)
Let ‘a’ and ‘b’ be the number of employees who voted for exactly one city and exactly two cities respectively. Each of the hundred employees voted for at least one of the three cities.
Therefore, we can say that
a + b = 100 … (1)
Also, a + 2b = 30 + 70 + 60
$\Rightarrow$ a + 2b = 160 … (2)
On solving equation (1) and (2) we can say that a = 40 and b = 60.
Therefore, the required ratio = 40 : 60 = 2 : 3.
12) Answer (B)
Let ‘x’ be the number of students who like both pepsi and coke but not coffee.
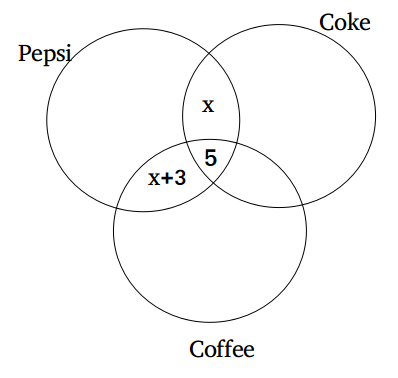
It is given that a total of 31 students like more than 1 beverage. Therefore, the number of students who like both coke and coffee but not pepsi = 31 – [(x)+(x+3)+(5)] = 23 – 2x.

It is also given that the number of students who like both coke and coffee is twice that of the number of students who like both pepsi and coffee.
$\Rightarrow$ 23-2x+5 = 2[(x+3)+(5)]
$\Rightarrow$ x = 3.
Therefore, the number of students who like both pepsi and coffee but not coke = x + 3 = 6. Hence, option B is the correct answer.
13) Answer (A)
If we carefully observe set A, then we find that $6^{2n} -35n – 1$ is divisible by 35. So, set A contains multiples of 35. However, not all the multiples of 35 are there in set A, for different values of $n$.
For $n = 1$, the value is 0, for $n = 2$, the value is 1225 which is the 35th multiple of 3.
If we observe set B, it consists of all the multiples of 35 including 0.
So, we can say that every member of set A will be in B while every member of set B will not necessarily be in set A.
Hence, option A is the correct answer.
14) Answer: 7
P = {1,2,3,4} and Q = {2,3,5,6,}
PΔQ = {1, 4, 5, 6}
R = {1,3,7,8,9} and S = {2,4,9,10}
RΔS = {1, 2, 3, 4, 7, 8, 10}
(PΔQ)Δ(RΔS) = {2, 3, 5, 6, 7, 8, 10}
Thus, there are 7 elements in (PΔQ)Δ(RΔS) .
hence, 7 is the correct answer.
15) Answer (D)
It has been given that among 200 students, 105 like pizza and 134 like burger.
The question asks us to find out the number of students who can be liking only burgers among the given values.
The least number of students who like only burger will be obtained when everyone who likes pizza likes burger too.
In this case, 105 students will like pizza and burger and 134-105 = 29 students will like only burger. Therefore, the number of students who like only burger cannot be less than 29.
The maximum number of students who like only burger will be obtained when we try to separate the 2 sets as much as possible.
There are 200 students in total. 105 of them like pizza. Therefore, the remaining 95 students can like only burger and 134-95 = 39 students can like both pizza and burger. As we can see, the number of students who like burger cannot exceed 95.
The number of students who like only burger should lie between 29 and 95 (both the values are included).
93 is the only value among the given options that satisfies this condition and hence, option D is the right answer.
DOWNLOAD APP FOR RRB FREE MOCKS
We hope this Venn Diagram Questions for RRB Group-D Exam will be highly useful for your preparation.





