Trigonometry Questions for RRB NTPC PDF
Download RRB NTPC Trigonometry Questions and Answers PDF. Top 15 RRB NTPC Maths questions based on asked questions in previous exam papers very important for the Railway NTPC exam.
Download Trigonometry Questions for RRB NTPC PDF
Take a free mock test for RRB NTPC
Download RRB NTPC Previous Papers PDF
Question 1: $\frac{2sinθ}{1+cosθ}$ = ?
a) 2cotθ/2
b) cotθ/2
c) tanθ/2
d) 2tanθ/2
Question 2: If $cosθ+\frac{1}{cosθ}=\frac{5}{2}$ , then find $cos^{2}θ+\frac{1}{cos^{2}θ}$ = ?
a) 25/4
b) 4/25
c) 4/17
d) 17/4
Question 3: $\frac{sinA+sinB}{cosA-cosB}$ = ?
a) -cot($\frac{A-B}{2}$)
b) -tan($\frac{A-B}{2}$)
c) cot($\frac{A+B}{2}$)
d) tan($\frac{A+B}{2}$)
RRB NTPC Previous Papers [Download PDF]
Question 4: It is known that 0 < θ < 90 and it is also given that sin θ = 3/5. Find the value of tan (θ/2)
a) 1/3
b) 3
c) 2/3
d) 3/2
Question 5: FInd cotθ+tanθ if sinθ = 5/13
a) 13/60
b) 60/13
c) 169/60
d) 60/169
Question 6: What is the maximum value of $\Large\frac{24}{25}$ sin θ + $\Large\frac{7}{25}$ cos θ + 5?
a) 4
b) 6
c) 5
d) 3
Question 7: What is the minimum value of 3 sin θ + 4 cos θ ?
a) 25
b) -25
c) 5
d) -5
Question 8: If cos θ = 40/41, then find the value of cot θ + tan θ ( 0 < θ < $90^\circ$) ?
a) $\Large\frac{1680}{360}$
b) $\Large\frac{360}{1680}$
c) $\Large\frac{1681}{360}$
d) $\Large\frac{360}{1681}$
Download General Science Notes PDF
Question 9: If cosec θ – cot θ = 3, then find cosec θ + cot θ = ?
a) $\Large\frac{1}{9}$
b) $\Large\frac{1}{27}$
c) $\Large\frac{1}{4}$
d) $\Large\frac{1}{3}$
Question 10: $ \Large \frac{sin 75 + sin 15}{cos 75 – cos 15}$ = ?
a) $ \sqrt{7}$
b) $ \sqrt{3}$
c) $-\sqrt{7}$
d) $- \sqrt{3}$
Question 11: It is known that 0 < θ < 90 and it is also given that $\cos θ = \frac{24}{25}$, then find the value of $ \tan(\frac{θ}{2})$?
a) $\Large\frac{1}{2}$
b) $\Large\frac{1}{5}$
c) $\Large\frac{1}{24}$
d) $\Large\frac{1}{7}$
Question 12: If $sin x = \dfrac{20}{29}$, then find the value of $sec x – tan x$
a) $\dfrac{2}{7}$
b) $\dfrac{4}{7}$
c) $\dfrac{3}{7}$
d) $\dfrac{1}{7}$
Question 13: If $sin x = \dfrac{20}{29}$, then find the value of $cosec x – cot x$
a) $\dfrac{2}{5}$
b) $\dfrac{4}{5}$
c) $\dfrac{7}{20}$
d) $\dfrac{8}{21}$
Daily Free RRB Online Tests for RRB Exams
Question 14: Find the value of $sin^2 1+sin^2 2+sin^2 3 +…..+sin^2 89$
a) $45.5$
b) $44.5$
c) $46.5$
d) $43.5$
Question 15: Find the value of $sec 1^\circ.sec 2^\circ.sec 3^\circ…..sec 179^\circ$.
a) 0
b) -1
c) 1
d) $\infty$
Download Current Affairs Questions & Answers PDF
Answers & Solutions:
1) Answer (D)
$\frac{2sinθ}{1+cosθ}$
= $\frac{2.2sinθ/2.cosθ/2}{2cos^2θ/2}$
= $\frac{2sinθ/2}{cosθ/2}$
= $2tanθ/2$
So the answer is option D.
2) Answer (D)
$cosθ+\frac{1}{cosθ}=5/2$
Squaring on both sides
$(cosθ+\frac{1}{cosθ})^2=(5/2)^2$
$cos^{2}θ+\frac{1}{cos^{2}θ}+2 = 25/4$
$cos^{2}θ+\frac{1}{cos^{2}θ} = 25/4-2 = (25-8)/4 = 17/4$
So the answer is option D.
3) Answer (A)
$\frac{sinA+sinB}{cosA-cosB}$
=$\frac{2sin(\frac{A+B}{2})cos(\frac{A-B}{2})}{-2sin(\frac{A+B}{2})sin(\frac{A-B}{2})}$
=-cot($\frac{A-B}{2}$)
So the answer is option A.
4) Answer (A)
Sinθ = 3/5 then cosθ = 4/5
$Tanθ/2 = \frac{sinθ}{1+cosθ} = \frac{3/5}{1+4/5} = \frac{3/5}{9/5} = \frac{3}{9} = 1/3$
So the answer is option A.
5) Answer (C)
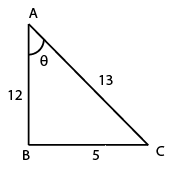
From the diagram, tanθ = 5/12, cotθ = 12/5
cotθ+tanθ = 12/5 + 5/12 = 169/60
So the answer is option C.
6) Answer (B)
For the expression asin θ + bcos θ + c,
The maximum value = $c+\sqrt{a^{2}+b^{2}}$ &
The minimum value = $c-\sqrt{a^{2}+b^{2}}$
for $\Large\frac{24}{25}$ sin θ + $\Large\frac{7}{25}$ cos θ + 5 , a = $\Large\frac{24}{25}$, b = $\Large\frac{7}{25}$, c = 5
maximum value = $ c + \sqrt{a^{2}+b^{2}}$
$= 5 + \Large\sqrt{ \frac{24}{25}^{2} + \frac{7}{25}^{2} } $
$= 5+1 = 6$
so the answer is option B.
7) Answer (D)
For the expression asin θ + bcos θ + c,
The maximum value = $c+\sqrt{a^{2}+b^{2}}$ &
The minimum value = $c-\sqrt{a^{2}+b^{2}}$
for 3 sin θ + 4 cos θ , a = 3, b = 4, c = 0
minimum value = $c-\sqrt{a^{2}+b^{2}}$
$= 0 – \sqrt{3^{2} + 4^{2}} = -\sqrt{25} = -5$
so the answer is option d.
8) Answer (C)
Given,
cos θ = $\Large\frac{40}{41}$
sin θ = $\Large\frac{9}{41}$
tan θ = $\Large\frac{9}{40}$ [As, tan θ = $\Large\frac{sin θ}{cos θ}$]
cot θ = $\Large\frac{40}{9}$
cot θ + tan θ = $\Large\frac{9}{40}$ + $\Large\frac{40}{9}$
= $\Large\frac{1681}{360}$
9) Answer (D)
We know that $ cosec^2 θ – cot^2 θ = 1$
$ (cosec θ – cot θ) ( cosec θ + cot θ) = 1$
Given cosec θ – cot θ = 3
$ \therefore 3 ( cosec θ + cot θ) = 1 $
cosec θ + cot θ = $\Large\frac{1}{3} $
10) Answer (D)
We know that,
$ \Large\frac{sinA+sinB}{cosA-cosB}$ = $ \Large\frac{2sin(\frac{A+B}{2})cos(\frac{A-B}{2})}{-2sin(\frac{A+B}{2})sin(\frac{A-B}{2})}$
= -cot($\frac{A-B}{2}$)
Here, A = 75; B = 15
Therefore,
$ \Large\frac{sin 75 + sin 15}{cos 75 – cos 15}$
= -cot($\Large\frac{75 – 15}{2}$)
= -cot($\Large\frac{60}{2}$)
= -cot 30
= $- \sqrt{3}$
11) Answer (D)
Given,
$\cos θ = \Large\frac{24}{25}$ then $\sinθ = \Large\frac{7}{25}$ & $\tanθ = \Large\frac{7}{24}$
$\tan(θ) = \Large\frac{2\tan(θ/2)}{1-\tan^{2}(θ/2)} $
$ \Large\frac{7}{24}$ = $\Large\frac{2\tan(θ/2)}{1-\tan^{2}(θ/2)} $
On solving we get,
$tan (θ/2) = \Large\frac{1}{7}$ $ or -7$
Since, 0 < θ < 90
$\tan(\frac{θ}{2}) = \Large\frac{1}{7}$
12) Answer (C)
Given $sin x = \dfrac{20}{29}$
⇒ $sin^2 x = \dfrac{400}{841}$
We know that $cos^2 x = 1-sin^2 x$
$cos^2 x = 1-\dfrac{400}{841}$
$= \dfrac{441}{841}$
$cos x= \dfrac{21}{29}$
$sec x = \dfrac{1}{cos x} = \dfrac{29}{21}$
$tan x = \dfrac{sin x}{cos x} = \dfrac{20}{21}$
$sec x – tan x = \dfrac{29}{21} – \dfrac{20}{21} = \dfrac{9}{21} = \dfrac{3}{7}$
13) Answer (A)
Given $sin x = \dfrac{20}{29}$
⇒ $sin^2 x = \dfrac{400}{841}$
We know that $cos^2 x = 1-sin^2 x$
$cos^2 x = 1-\dfrac{400}{841}$
$= \dfrac{441}{841}$
$cos x= \dfrac{21}{29}$
We know that $cot x = \dfrac{cos x}{sin x}$
$= \dfrac{21}{20}$
$cosec x = \dfrac{1}{sin x} = \dfrac{29}{20}$
$cosec x – cot x = \dfrac{29}{20} – \dfrac{21}{20} = \dfrac{29-21}{20} = \dfrac{8}{20} = \dfrac{2}{5}$
14) Answer (B)
We can write $sin^2 89 as sin^2 (90-1) = cos^2 1$
$sin^2 88 = sin^2 (90-2) = cos^2 2$
In the same way, $sin^2 46 = sin^2 (90-44) = cos^2 44$
Hence, the given equation can be written as,
$sin^2 1+cos^2 1+sin^2 2+cos^2 2+…..sin^2 45$
$= 1+1+1+1….+\dfrac{1}{2}$
Here, the number of 1’s will be $44$ as there are $88$ terms in the form of $sin^2 x$ and $cos^2 x$.
Hence, Required answer $= 44+\dfrac{1}{2} = 44.5$
15) Answer (D)
$sec 1^\circ.sec 2^\circ.sec 3^\circ…..sec 179^\circ = sec 1^\circ.sec 2^\circ.sec 3^\circ……sec 90^\circ…..sec 179^\circ$
We know that $sec 90^\circ = \infty$
Therefore, The given series multiplication becomes $\infty$.
DOWNLOAD APP FOR RRB FREE MOCKS
We hope this Trigonometry Questions for RRB NTPC Exam will be highly useful for your Preparation





