Most expected Top 100 Quant Questions for TISSNET and CMAT 2022

Here you can download 100 Quant – Questions for TISSNET and CMAT PDF by Cracku. Very Important  100 Quant – Questions for TISSNET and CMAT based on asked questions in previous exam papers. These questions will help your TISSNET and CMAT preparation. So kindly download the PDF for reference and do more practice.

Download 100 quant questions for TISSNET and CMAT

Enroll to CMAT crash course

Get 5 TISSNET mocks at just Rs.299

Take CMAT mock tests here

Question 1: A shopkeeper claims to sell rice at cost price. He uses a false weight with the intention of selling rice at 25% profit. After selling Rice to a customer, he realizes that the customer has paid 10% less than what he should have paid. What is the actual profit percentage made by the shopkeeper?

a) 6.25%

b) 10%

c) 12.5%

d) 15%

Question 2: If 15 August 1905 was a Tuesday, which day was 15 August in 1895?

a) Friday

b) Wednesday

c) Thursday

d) Tuesday

Question 3: A shopkeeper marks his books at 25% above the cost price. Due to slump in the market, his cost reduces by 5%. And then,to boost his sale, he offered a discount of 8% due to which sales goes up by 25%. Compute the change in the shopkeepers profit.

a) No change

b) 7% change

c) 2.5% change

d) 8% change

Question 4: A company publishes to its customers that at a certain compound interest rate, a sum of money deposited by anyone will become 8 times in 3 years. If the same amount is deposited at the same compound rate of interest, then in how many years will it become 16 times ?

a) 4 years

b) 3.5 years

c) 3 years

d) 4.5 years

Question 5: What is the farthest distance between two points on a cylinder of: HEIGHT 8 and RADIUS 8 ?

a) $8\sqrt{5}$

b) $16\sqrt{5}$

c) $8\sqrt{2}$

d) $8\sqrt{3}$

Question 6: The work done by a man, woman and child are in the ratio 3: 2:1. If daily wages of 20 men, 30 women and 36 children amount to 78/-, what will be the wages of 15 men, 21 women and 30 children for 18 weeks ?

a) 7371/-

b) 8645/-

c) 7532/-

d) 9000/-

Question 7: The sum of two numbers is 135 and their HCF is 9. How many such pairs of numbers can be formed ?

a) 2

b) 5

c) 4

d) 6

Question 8: There are 6 tasks and 6 persons. Task 1 cannot be assigned either to person 1 or person 2. Task 2 must be assigned to either person 3 or person 4. Every person is to be assigned one task. In how many ways can the assignment be done ?

a) 360

b) 192

c) 144

d) 180

Question 9: The following table gives the percentage distribution of population of five states, P, Q, R, S and T on the basis of poverty line and gender. If the male population above poverty line for state R is 1.9 million, then the total population of state R is?

a) 6.25 million

b) 5.35 million

c) 4.5 million

d) 4.85 million

Question 10: In how many ways a committee consisting of 5 men and 6 women can be formed from 8 men and 10 women ?

a) 5041

b) 5040

c) 11670

d) 11760

Get 5 CMAT mocks at just Rs.299

Download CMAT Previous Papers PDF

Question 11: In a certain town, 40% of people have brown hair, 30% of people have brown eyes and 12% have both brown hair and brown eyes.
How many people in town have neither brown hair nor brown eyes ?

a) 44%

b) 43%

c) 41%

d) 42%

Question 12: The angle created by two hands of a clock when the clock shows 5.20 P.M. is :

a) 40°

b) 60°

c) 35°

d) 40

Question 13: X and Y are running towards each other from their houses. X can reach Y’s house in 25 minutes which is half the time taken by Y to run from his house to X’s house. If the two start to run towards each otherat the same time, then how much more time it will be required by Y to reach the middle of houses ?

a) 18 min.

b) 25 min.

c) 50 min.

d) 12.5 min.

Question 14: In a test the average marks obtained by boys and girls in a class are 72 and 56 respectively. The average marks obtained by the class in the same test is 60. If in an other test the average marks obtained by the boys and girls are 64 and 80 respectively, what is the average marks obtained by the class in the test?

a) 76

b) 74

c) 72

d) 70

Question 15: Riaz distributes 20 copies of The Hindu and 25 copies of Deccan Chronicle in an apartment building that has 40 apartments. If he distributes at least one newspaper to each apartment, the number of apartments that buy only The Hindu is

a) 5

b) 20

c) 15

d) Cannot say

Question 16: The geometric mean proportion between  $30 + \sqrt200$ and $54 – \sqrt648$ is:

a) $6\sqrt2$

b) $4\sqrt5$

c) $6\sqrt{35}$

d) $5\sqrt6$

Question 17: Mohit was looking for his father. He went 90 meters to the East before turning to his right. He went 20 meters before turning to his right again to look for his father in his uncle’s house 30 meters away from this point. His father was not there. From here he went 100 meters to the North before meeting his father in a street. How far away did the son meet his father from the starting point?

a) 140 meters

b) 260 meters

c) 100 meters

d) 80 meters

Question 18: There are six teachers. Out of them, two teach physics, other two teach Chemistry and the rest two teach Mathematics. They have to stand in a row such that Physics, Chemistry and Mathematics teachers are always in a set. The numberof ways in which they can do, is :

a) 24

b) 48

c) 36

d) 12

Question 19: The monthly incomes of Amit and Bharat are in the ratio of 5:4, their monthly expenses are in the ratio of 19:21, and their monthly savings are in the ratio of 37:18. If the total annual savings of Amit and Bharat is Rs.1,32,000, Amit’s monthly income is:-

a) Rs. 12,000

b) Rs. 15,000

c) Rs. 18,000

d) Rs. 16,000

Question 20: Simplify the following: $\frac{0.3 \times 0.3 + 0.03 \times 0.03 – 0.6 \times 0.03}{0.54}$

a) 0.03

b) 0.135

c) 0.982

d) 9.37

Download TISSNET Previous Papers PDF

Take TISSNET Mock Tests

Question 21: Find the smallest number by which 2400 should be divided to make it a perfect cube.

a) 220

b) 385

c) 260

d) 300

Question 22: A man of height 2m is standing at a certain distance from a lamppost of height 10m. The angle of elevation of the tip of the shadow is 30 degrees. The man walks towards the lamppost and the angle of elevation of the tip of the shadow is now 60 degrees. Find the distance walked by the man.

a) $8/\sqrt3$

b) $16\sqrt3$

c) $16/\sqrt3$

d) $8\sqrt3$

Question 23: Sarvesh and Kamlesh run on the circular track of circumference 900 m. Initially, they are diametrically opposite to each other. Their speeds are 45 m/s and 30 m/s. If $T_{1}$ is the time taken till 2nd meeting when they run in the same direction and $T_{2}$ is the time taken till 2nd meeting when they run in opposite directions then find out $T_{1}$:$T_{2}$?

a) 4: 1

b) 3: 1

c) 5: 1

d) None of the above

Question 24: In how many different ways, can the letters of the words EXTRA be arranged so that the vowels are never together ?

a) 168

b) 48

c) 120

d) 72

Question 25: In a triangle ABC, AD is the bisector of angle A. If AC =4.2 cm, DC = 6 cm, BC =10 cm, find AB.

a) 2.7 cm

b) 2.9 cm

c) 2.8 cm

d) 3.4 cm

Question 26: In a building there are 30 cylindrical pillars. The radius of each pillar is 35 cm and height is 5 m. Find out the cost of painting the curved surface of half the number of pillars. The rate of painting is Rs. 10 per $m^2$.

a) Rs. 16,500

b) Rs. 8250

c) Rs. 1650

d) Rs. 4125

Question 27: A management institute has 6 senior professors and 4 junior professors, 3 professors are selected at random for a government project. The probability that at least one of the junior professors would get selected is :

a) 2/3

b) 1/5

c) 5/6

d) 1/6

Question 28: If f(x) is a polynomial satisfying f(x)f($\frac{1}{x}$)= f(x)+f($\frac{1}{x}$), f(2) = 9 then find the value of f(5)?

a) 125

b) 26

c) 126

d) 25

Question 29: Of the 850 students who wrote an entrance examination at a center, 550 did very well in the Mathematics and Logical reasoning paper, 600 did very well in English language proficiency and 350 did very well in both. How many students did not do very well in Mathematics and Logical reasoning?

a) 300

b) 650

c) 50

d) 250

Question 30: In a survey conducted among 120 houses, it was found that 50 read Times of India, 60 read Indian Express and 48 read Hindustan Times; 20 read Times of India and Indian Express, 18 read Times of India and Hindustan Times and 24 read Indian Express and Hindustan Times. If 10 read all three, how many read only one
newspaper?

a) 50

b) 32

c) 64

d) 84

Take CMAT Mock Tests

Download CMAT previous papers PDF

Question 31: Given: Anuj takes 1 day to complete a job. Bharat takes twice the time as Anuj to complete the same job. Chetan takes twice the time as Bharat to complete that job. Dhiraj takes twice the time as Chetan to complete that job.
(A) Chetan and Dhiraj will take 8/3 days to complete the work
(B) The second fastest pair to complete the work is Anuj and Dhiraj
(C) The second slowest pair to complete the work is Bharat and Dhiraj
(D) Bharat and Dhiraj will take 4/3 days to complete the work

a) (A), (B) and (C) only

b) (A) and (D) only

c) (A) and (C) only

d) (A) only

Question 32: Given below are two statements
Statement I : $(543)_6$ is equivalent to $(317)_8$
Statement II : The last 4 bits in the binary representation of a multiple of 16 is 1000.
In light of the above statements, choose the correct answer from the options given below

a) Both Statement I and Statement II are true

b) Both Statement I and Statement II are false

c) Statement I is true but Statement II is false

d) Statement I is false but Statement II is true

Question 33: A type 1 tap can fill an empty tank in 4 hours. A type 2 tap can empty a full tank in 3 hours. There are a total of 10 taps. A few of them are type 1 taps and all the others are type 2 taps. If an empty tank gets filled in 6 hours, which of the following can be the value of the number of type 1 taps in the group?

a) 4

b) 5

c) 6

d) 7

Question 34: Rajesh can check the quality of 1000 items in 5 hours and Rakesh can complete 75% of the same job in 3 hours. How much time is required for both of them to check 1300 items, if Rakesh stops checking after 2 hours ?

a) 1 hour

b) 2 hours

c) 4 hours

d) 3 hours

Question 35: On a certain day when interviews for Master Degree courses were going on, it was found that 35 students attended interviews for MA Education, 47 students attended interviews for MSW and among the 2 groups, 12 students attended both. What is the total number of students who attended either of the interviews?

a) 82

b) 70

c) 94

d) 58

Question 36: The cost price of a pen is Rs 20. A shopkeeper sells the first pen at Rs 3, the second pen at Rs 5, the third pen at Rs 7 and so on. What is the number of pens that the shopkeeper has to sell so as to make a total profit of 10%?

a) 19

b) 20

c) 21

d) 22

Question 37: If N = $2^8\times\ 9^2\times\ 5^3$, then the number of factors of N which are multiples of 25  is

a) 54

b) 72

c) 90

d) 80

Question 38: The speed of a boat in still water is 5 km/hr. If it takes thrice as much time in going 20 km upstream as in going the same distance downstream, find the speed of the stream.

a) 5.5 km/hr

b) 2.5 km/hr

c) 3.5 km/hr

d) 4.5 km/hr

Question 39: What are the maximum and minimum values of the expression $\frac{x}{x^2 – 3x + 4}$?

a) 1, 10/11

b) 10/11, -1/7

c) 1, -1/7

d) None of the above

Question 40: If $sin A$ = $\dfrac{1}{4 cosA}$, what is the value of $tan 4A$?
Assume that $A$ lies between 0 and 45 degrees.

a) $\sqrt{3}$

b) $\frac{1}{\sqrt{3}}$

c) $1$

d) Cannot be determined

Take TISSNET Mock Tests

Download TISSNET previous papers PDF

Question 41: In a school, 200 students play at least one of Football, Cricket and Hockey. 120 students play Cricket, 60 students play Football and 80 students play Hockey. 20 students play all the three games. Find the number of students that play at least two sports.

a) 80

b) 60

c) 40

d) 20

Question 42: In a group consisting of 80 people, 20 people read Sportly Weekly, 40 people read Sportstar and 33 people read Illustrated Weekly. If each person in the group reads at least one magazine, what is the minimum number of people in the group who read all the three magazines?

a) 12

b) 10

c) 5

d) 0

Question 43: It costs Rs. 6000/- and Rs. 6,100- respectively to paint the 4 walls of 2 square halls, of the same height. If the length of one hall exceeds the length of the other by 1 m and the cost of painting is Rs. 5 per sq.m., what is the height of the two walls ?

a) 10 m

b) 7.5 m

c) 3 m

d) 5 m

Question 44: A triangle is drawn on a clock face connecting 1, 6 and 11. What are the angles of the triangle?

a) 75, 75, 30

b) 60, 60, 60

c) 30, 60, 90

d) None of these

Question 45: The maximum value of 3 $cosx+4 sinx+8$ is

a) 15

b) 3

c) 13

d) 7

Question 46: How many ten-digit numbers can be formed using all the digits of 2435753228 such that odd digits appear only in even places?

a) $2!3!5!$

b) $(5!)^{2}$

c) $\frac{(5!)^{2}}{3!}$

d) $\frac{(5!)^{2}}{3!(2!)^{2}}$

Question 47: Which of the following dates fall on the same day of the week in any given month?

a) 4 and 24

b) 6 and 30

c) 13 and 27

d) 11 and 22

Question 48: Vijay borrows Rs.10,000 from Akram at 8% p.a simple interest. He lends Rs. 5000 to Rajnish at 10% p.a. simple interest and Rs.5000 to Kamal at 10% p.a compound interest compounded annually. If all the persons pay the amount along with the interest back by the end of 2 years, the net profit earned by Vijay is

a) Rs.350

b) Rs.450

c) Rs.550

d) Rs.650

Question 49: Students in a commerce class took a test. The average score of men is 70 and of women is 83. The class average is 76. What is the ratio of men to women in the class?

a) 8:7

b) 7:8

c) 7:6

d) 6:7

Question 50: How much time does Mr.Surya take to cover a distance of 500 m if he runs at a speed of 25 km/hr?

a) 35 sec

b) 80 sec

c) 60 sec

d) 72 sec

Enroll to CAT 2022 course

Download CMAT Previous Papers PDF

Question 51: Brother and sister both appear for an interview. The probability of the selection of brother is $\frac{1}{8}$ while the probability of rejection of sister is $\frac{4}{5}$ What is the probability that only one of them is selected ?

a) $\frac{11}{40}$

b) $\frac{7}{40}$

c) $\frac{5}{13}$

d) $\frac{1}{10}$

Question 52: Which of the following sets of numbers can be used as the lengths of the sides of a triangle ?

a) [5, 7, 12]

b) [5, 7, 9]

c) [7, 9, 17]

d) [2, 4, 10]

Question 53: If the G.M. and A.M. of two numbers are in the ratio 3:5, the numbers are in the ratio

a) 4:5

b) 3:5

c) 1:3

d) 1:9

Question 54: If f(x) = $x^3 – 4x + p$ and f(0) and f(1) are of opposite signs, Which one of the following is neccessarily true?

a) -1 < p < 2

b) 0 < p < 3

c) -2 < p < 1

d) -3 < p < 0

Question 55: Two oranges, three bananas and four apples cost Rs. 15. Three oranges, two bananas and one apple cost Rs. 10. I bought 3 oranges, 3 bananas and 3 apples. How much did I pay ?

a) Rs. 10

b) Rs. 8

c) Rs. 15

d) Cannot be determined

Question 56: Five years ago, the average age of A,B,C and D was 45 years. By including X in the present lot their present average changes to 49 years. What is the present age of X?

a) 40 years

b) 45 years

c) 49 years

d) 48 years

Question 57: Find the remainder when the number $3^{85}$ is divided by 51.

a) 1

b) 13

c) 26

d) 39

Question 58: The present ages of Ram and Shyam are in the ratio 6:7. 14 years ago the ratio of the ages of the two was 4:5. What will be the ratio of their ages 21 years from now?

a) 9:10

b) 8:9

c) 7:9

d) 10:11

Question 59: The LCM and HCF of two numbers are 84 and 21 respectively. If the ratio of two numbers is 1 : 4, then the larger among two numbers is:

a) 28

b) 48

c) 88

d) 84

Question 60: A sum of money lent at simple interest amounts to Rs. 880 in 2 years and to Rs. 920 in 3 years. What is the sum of money?

a) 700

b) 760

c) 784

d) 800

Enroll to CAT 2022 Complete course

Download TISSNET Previous Papers PDF

Question 61: If $y^2$ + 3y – 18 ≥ 0, which of the following is true?

a) y ≤ 3 or y ≥ 0

b) y > – 6 or y < 3

c) -6 ≤ y ≤ 3

d) y ≥ 3 or y ≤ – 6

Question 62: If machine A needs 2 hours to finish a work, machine B 3 hours and machine C 6 hours to finish the same work, how long will it take for machines A, B and C to complete the work if they work simultaneously?

a) 15 minutes

b) half an hour

c) 1 hour

d) 1 hour 15 minutes

Question 63: A tank has 3 inlet pipes and 2 outlet pipes. The inlet pipes can individually fill the tank in 4, 6 and 8 hours. The outlet pipes can individually empty the tank is 2 hours and 10 hours. Find the time in which the empty tank gets filled, if all the taps are kept open.

a) 30 hours

b) 24 hours

c) 36 hours

d) None of the above

Question 64: Two pipes A and B can fill a cistern in 120 minutes and 150 minutes respectively. There is also an outlet C.If all the three pipes are opened together, the cistern gets filled in 100 minutes. How much time will be taken by C to empty full tank?

a) 3 h 20 min

b) 2 h 40 min

c) 3 h

d) 3 h 40 min

Question 65: On a square cardboard of length 10 cm, two identical circles of radius 2 cm are drawn such that the two centres and the two points of intersection of the circle form a square. Find the total area of the cardboard covered by the two circles?

a) 4$\pi$ + 6

b) 6$\pi$ – 4

c) 4$\pi$ + 4

d) 6$\pi$ + 4

Question 66: How many times do the hands of a clock overlap in 24 hours?

a) 11

b) 22

c) 24

d) 12

Question 67: In a class there were 10 students and the average weight of the students in the class was 54.5 kg. Five students weighing 89 kg, 46 kg, 82 kg, 93 kg and 60 kg joined the class one by one. After the addition of every student, the average weight (in kg) of the class was an integer. If the weight of the first student that joined was 82 kg, then what was the average weight (in kg) of the class after the 4th student joined?

Question 68: What is the 150th letter in the series a, b, b, c, c, c, d, d, d, d, . . .

a) o

b) p

c) q

d) r

Question 69: From a jar of wine containing 32 litres, 4 litres is drawn out, and the jar is filled up with water. If the same proportion of wine is further drawn out two more times, what proportion of wine to water will be there in the resulting mixture?

a) 245:166

b) 343:169

c) 363:173

d) 323:189

Question 70: In a circle of radius 6 cm, arc AB makes an angle of 114° with centre of the circle O.
What is angle ABO?

a) 23°

b) 42°

c) 38°

d) 33°

Enroll to CMAT crash course

Get 5 TISSNET mocks at just Rs.299

Take CMAT mock tests here

Question 71: 25,000/- is borrowed at compound interest at the rate of 3% for first year, 4% for $2^{nd}$ year and 5% for $3^{rd}$ year. Find the amount to be paid after 3 years.

a) 28,117/-

b) 28,118/-

c) 28,120/-

d) 28,119/-

Question 72: In a 1000 metre race, Rahul reaches the finishing line 5 seconds before than Raj and beats Raj by 50 metre. What is Rahul’s speed (in m/s)?

a) $11\frac{9}{19}$

b) $9\frac{9}{19}$

c) $10\frac{10}{19}$

d) $9\frac{10}{19}$

Question 73: Given ‘$y$’ is a natural number, how many values of “$y$” are possible for $(y^2 – 5y + 5)^{(y – 8)(y + 6)} = 1$?

a) 4

b) 1

c) 3

d) 2

Question 74: Three solid cubes of sides 1 cm, 6 cm and 8 cm are melted to form a new cube. Find the surface area of the cube so formed.

a) 729 $cm^2$

b) 486 $cm^2$

c) 125 $cm^2$

d) 529 $cm^2$

Question 75: Father’s age and daughter’s age add upto 55. Daughter’s age is reverse of her father’s and difference in their ages is more than 10. How old is the daughter?

a) 21

b) 14

c) 23

d) 32

Question 76: If x : y = 2 : 3, the value of (3x + 2y) : (2x + 5y) is:

a) $\frac{12}{25}$

b) $\frac{11}{27}$

c) $\frac{11}{15}$

d) $\frac{12}{19}$

Question 77: Given two integers, x and y, which of the following statements is true?

a) if $x^n$ > $y^n$, then it necessarily follows that x > y (‘n’ is an odd natural number)

b) if $x^n$ > $y^n$, then it necessarily follows that x > y(‘n’ is an even natural number)

c) if $x^2$ > $y^2$, then it necessarily follows that $x^3$ > $y^3$

d) None of the above

Question 78: If the compound interest on a sum of Rs 5000 at a rate of 5% p.a. is Rs 788, what is the time for which the investment was made?

a) 5 years

b) 4 years

c) 2 years

d) 3 years

Question 79: What is the probability of drawing a king or a heart from a deck of cards ?

a) 1/13

b) 1/52

c) 17/15

d) 4/13

Question 80: Among a group of children, 6 children like only chocolate ice cream and 5 children like only butter scotch ice cream and 5 like either of the two. If each child gets an ice cream, how many ice creams should we order?

a) 11

b) 21

c) 16

d) 6

Enroll to CMAT crash course

Question 81: If one third of one-fourth of a number is 15, then three-tenth of that number is

a) 61

b) 54

c) 46

d) 38

Question 82: In triangle PQR. PS is perpendicular to QR and S divides QR in the ratio of 3 : 1 internally. If PQ=21 and PR =9,find QR.

a) $18\sqrt{5}$

b) $16\sqrt{5}$

c) $15\sqrt{5}$

d) $12\sqrt{5}$

Question 83: Ramesh bought two machine paying Rs. 1500 and Rs.1000 respectively. Every year, the machines depreciate 10% and 15% of their value at the beginning of the year. What is the total value depreciated at the end of two years?

a) Rs. 625

b) Rs. 562.5

c) Rs.550

d) Rs. 600

e) 625.5

Question 84: A rectangular field has an area of 20 sq. km. If the perimeter of the field is 18 km, what is the length of the longer side of the field?

a) 10 km

b) 3 km

c) 8 km

d) 5 km

Question 85: Tom’s salary is 150% of John’s salary. John’s salary is 80% of Steve’s salary. What is the ratio of Steve’s salary to Tom’s salary ?

a) 4 : 5

b) 5 : 4

c) 6 : 5

d) 5 : 6

Question 86: Ramesh invests Rs. 1400 in an account that earns simple interest. After 9 months, the balance is Rs. 1421. What is the annual interest rate?

a) 2%

b) 5%

c) 1%

d) 8%

Question 87: If $\tan A + \cot A = \sqrt 5$, What is the value of $\tan^3 A + \cot ^3 A$?

a) $\sqrt5$

b) 3

c) $2\sqrt5$

d) $\frac{2}{\sqrt5}$

Question 88: Two sheep are tied at the two ends of a diagonal of a square field of length 10 metres. The lengths of both the ropes are equal and they can both just touch each other when stretched to the fullest. What is the maximum area both the sheep can graze in total?

a) 21$\pi$ sq m

b) 25$\pi$ sq m

c) 24$\pi$ sq m

d) $75 sq m$

Question 89: The length of the minute of a watch is 42 mm. The area swept by it in 30 minutes (in $mm^2$) by taking π as 3.14 is:-

a) 2769.5

b) 44 π

c) 728

d) 1040 π

Question 90: X is a number such that 65% of X is more than its 36% by 2900. What is 122% of the number X?

a) 10000

b) 11000

c) 13420

d) 12200

Get 5 CMAT mocks at just Rs.299

Download CMAT Previous Papers PDF

Question 91: In how many different ways can 3 red balls, 2 blue balls and 4 yellow balls be arranged so that the balls of the same color come together?

a) 1742

b) 1732

c) 1728

d) 1750

Question 92: A and B working together finish a work in 6 hours. A can finish the work in 10 hours. How long will it take for B to finish the same work alone?

a) 15 hours

b) 16 hours

c) 18 hours

d) 24 hours

Question 93: Meera and Sarika attempted to solve a quadratic equation in x. Sarika made a mistake in reading the coefficient of x and obtained the roots as 12 and 16. Meera made a mistake in reading the constant term of the equation. She obtained the roots as-22 and – 6. The corrects root(s) is (are) :
(A) -16
(B) -12
(C) 12
(D) 16

Choose the correct answer from the options given below:

a) (A) and (B) only

b) (A) and (C) only

c) (C) and (D) only

d) (B) and (D) only

Question 94: Anil is twice as good a student as Bharat and is able to finish a work in 30 minutes less than Bharat’s time. Find the time in which both of them can finish the same work together?

a) 45 min

b) 30 min

c) 25 min

d) 20 min

Question 95: If log 625 = 2.796, then the value of log 25 is

a) 1.398

b) 1.698

c) 1.295

d) 2.125

Question 96: If a is between 0 and 1, which of the following statements is (are) true?
(i) $a^2$ – 1> 0
(ii) $a^2$ + 1 > 0
(iii) $a^2$ – a > 0

a) only (ii)

b) (i) & (ii)

c) (iii) only

d) All three

Question 97: If (x + 4) is a factor of $x^3 + 2x^2 + bx + 68$, what is the value of b?

a) -9

b) 9

c) 8

d) -8

Question 98: In a larger circular pool of 20 feet diameter, two frogs start swimming from east and west ends of the pool (named A & C respectively) towards a worm on the northern edge of the pool at point B. What is the measure of the angle ABC?

a) 20 degrees

b) 70 degrees

c) 90 degrees

d) 30 degrees

Question 99: A certain amount of money is divided amongst three friends, Amar, Akbar and Anthony in the ratio $2 : 3 : 7$ respectively. If Anthony gets Rs. 15 more than Amar, how much money does Akbar get?

a) 36

b) 9

c) 25

d) 6

Question 100: ABC is an isosceles triangle with AB = AC. The vertex angle A measures eight times the measure of a base angle. AD is the angle bisector of vertex angle A. What is the measure of the angle BAD?

a) $144^\circ$

b) $81^\circ$

c) $72^\circ$

d) $42^\circ$

Enroll to CMAT crash course

Get 5 TISSNET mocks at just Rs.299

Take CMAT mock tests here

Answers & Solutions:

1) Answer (C)

Let cost price be 1000 per Kg of rice
Now to make 25% profit at 1000
He will sell 800 gm of rice
Now C.P of 800 gm of rice = 800
Now he sold at 10% less than 1000 so S.P = 900
Now therefore profit = $\frac{900-800}{800}\times\ 100\ =\ \frac{100}{8}=12.5\ \%$

2) Answer (C)

Number of odd days between 15 Aug 1895 to 31 Dec 1895 = $16+2+3+2+3=26$

Number of odd days between 01 Jan 1896 and 31 Dec 1904 = $2+1+1+1+1+1+1+1+2=11$

Number of odd days between 01 Jan 1905 to 15 August 1905 = $3+0+3+2+3+2+3+15=31$

=> Total odd days = $(26+11+31)\%7=5$

So, the 15th August 1895 is a Thursday

3) Answer (A)

Let cost price of each article = Rs. 100 and number of articles sold be $x$

=> Original selling price price = Rs. 125

=> Original profit = Rs. $(125-100)x = Rs.$ $25x$

After offering discount of 8%, => New selling price = $\frac{92}{100}\times125=Rs.$ $115$

Also, new cost price = $\frac{95}{100}\times100=Rs.$ $95$

$\because$ Sale increases by 25%, => Number of articles now sold = $1.25x$

=> New profit = Rs. $(115-95)\times1.25x = Rs.$ $25x$

$\therefore$ There is no change in profit.

=> Ans – (A)

4) Answer (A)

If a sum of money becomes $x$ times in $a$ years, it will become $y$ times in $b$ years

=> $(x)^{\frac{1}{a}}=(y)^{\frac{1}{b}}$

Similarly, $(8)^{\frac{1}{3}}=(16)^{\frac{1}{t}}$

=> $(2)^{\frac{3}{3}}=(2)^{\frac{4}{t}}$

=> $1=\frac{4}{t}$

=> $t=4$ years

=> Ans – (A)

5) Answer (A)

Height of cylinder = 8 units and radius = 8 units

=> Farthest distance = hypotenuse = $\sqrt{(8)^2+(16)^2}$

= $8\sqrt{5}$ units

=> Ans – (A)

6) Answer (A)

Let the efficiency of a man, woman and child be $3x,2x,x$ espectively.

Thus, 1 day wage = $(3x\times20)+(2x\times30)+(x\times36)=78$

=> $156x=78$

=> $x=\frac{1}{2}$

$\therefore$ Wages of 15 men, 21 women and 30 children for 18 weeks = $[(15\times3x)+(21\times2x)+(30\times x)]\times18\times7$

= $117\times\frac{1}{2}\times126$

= $117\times63=Rs.$ $7,371$

=> Ans – (A)

7) Answer (C)

Let the two numbers be $9x$ and $9y$, where $x$ and $y$ are co prime numbers.

=> $9x+9y=135$

=> $x+y=\frac{135}{9}=15$

Now, pairs of natural numbers having sum 15 and co prime are = (1,14), (2,13), (4,11), (7,8)

Thus, 4 such pairs can be formed.

=> Ans – (C)

8) Answer (C)

Based on the given constraints, there will be two cases in which task 1 is either assigned to one among person 3 or 4 or to one among person 5 or 6

Case 1:

Assigning Task 1 to either Person 3 or 4.

No. of ways of assigning task 1 = 2 ways

No. of ways of assigning task 2 = 1 way

Remaining 4 tasks can be assigned among the remaining 4 persons in 4! ways.

Therefore, Total number of ways = 2 x 1 x 4! = 48

Case 2:

Assigning Task 2 to either Person 5 or 6.

No. of ways of assigning task 1 = 2 ways

No. of ways of assigning task 2 = 2 ways

Remaining 4 tasks can be assigned among the remaining 4 persons in 4! ways.

Therefore, Total number of ways = 2 x 2 x 4! = 96

Hence, total number of possible arrangements= 48 + 96 = 144

9) Answer (A)

Let total population of state R = $100x$ million

% of people below poverty line in state R = $24x$ and above poverty line = $76x$

Males above poverty line = $\frac{2}{5}\times76x=1.9$

=> $x=\frac{0.5}{8}=0.0625$

$\therefore$ Total population of state R = 6.25 million

=> Ans – (A)

10) Answer (D)

Number of ways a committee consisting of 5 men and 6 women can be formed from 8 men and 10 women

= $C^{10}_6\times C^8_5$

= $C^{10}_4\times C^8_3$

= $\frac{10\times9\times8\times7}{1\times2\times3\times4}\times\frac{8\times7\times6}{1\times2\times3}$

= $(10\times3\times7)\times(8\times7)$

= $210\times56=11760$

=> Ans – (D)

11) Answer (D)

Let total number of people in the town = $100x$

People who have both brown hair and eyes = $b=12x$

=> People who have brown hair = $a+b=40x$

=> $a=28x$

Similarly, $c=18x$

$\therefore$ People who have neither brown hair nor brown eyes = $100x-(12x+18x+28x)=42\%$

=> Ans – (D)

12) Answer (D)

In a clock,

In one revolution the minute hand covers 60°

$\Rightarrow$ 60 minutes = 360°

$\Rightarrow$ 1 minute = 6°.

$\Rightarrow$ for every minute the minute hand covers 6°.

Similarly In one revolution the hour hand covers 12 hours.

$\Rightarrow$ 12 hours = 360°

$\Rightarrow$ 1 hour = 30°.

$\Rightarrow$ for every hour, the hour hand covers 30°.

So at 5.20 P.M. the hour hand must have covered 5 * 30° = 150° + 20*1/2 = 160

and minute hand must have covered 20 * 6° = 120°.

So the angle created by two hands of the clock when the time is 5.20 P.M. = 160 – 120 = 40°.

13) Answer (D)

Time taken by X to reach Y’s house = 25 minutes and by Y to reach X’s house = 50 min

Ratio of time taken = $1:2$

$\because$ speed is inversely proportional to time, let speed of X = $2x$ km/min and speed of Y = $x$ km/min and distance between their houses = $2d$ km

Using, speed = distance/time

=> $x=\frac{2d}{50}=\frac{d}{25}$

=> $\frac{d}{x}=25$ ————-(i)

Now, time taken by Y to travel $d$ km, i.e. mid way = $\frac{d}{x}$

= $25$ minutes

Now, time taken by X to travel $d$ km, i.e. mid way = $\frac{d}{2x}$

= $12.5$ minutes

So, the correct answer is $25-12.5=12.5$ minutes

=> Ans – (D)

14) Answer (A)

Ratio of boys to girls in the class can be obtained using the method of alligation.
Ratio of boys to girls is
(60-56) : (72-60)
= 4 : 12
= 1 : 3

In the second test, the average marks obtained by boys and girls are 64 and 80 respectively.
Average marks obtained by the class = [(64*1)+(80*3)]/4 = 304/4 = 76

Hence Option A.

15) Answer (C)

Let a = Apartments where only Hindu was distributed

b = Apartments where the only DC was distributed

c= both

a+c = 20

b+c = 25

a+b+c = 40

=> b= 20,a=15 and c= 5

Only hindu =15

16) Answer (C)

The geometric mean proportion between two numbers ‘a’ and ‘b’ is given by $\sqrt{a\times b}$

The given two numbers are 30 + $\sqrt200$ and 54 – $\sqrt648$

which are also equal to 10(3+$\sqrt2$) and 18(3-$\sqrt2$).

Hence the geometric mean proportion = $\sqrt {10(3+\sqrt2)\times 18(3-\sqrt2)}$ = $\sqrt {180\times (3^2 – (\sqrt2)^2)}$ = $\sqrt {1260}$ = $6\times \sqrt35$.

17) Answer (C)

The following diagram shows his path:

Using Pythagoras theorem, we can see that his actual displacement is 100m from the starting point to the finishing point.

18) Answer (B)

There are 2 physics teacher.They can stand in a row in $P(2,2)=2!=2\times1=2$ ways

Similarly, the two Chemistry and Mathematics teacher can stand in 2 ways each.

These three sets can be arranged in themselves in $3!=3\times2\times1=6$ ways

=> Required number of ways = $2\times2\times2\times6=48$

=> Ans – (B)

19) Answer (B)

Given monthly savings of Amit and Bharat are in the ration 37:18. Let the savings of Amit and Bharat be 37k and 18k, where ‘k’ is a constant.

$\Rightarrow$ Total  monthly  savings  of  Amit  and  Bharat = 55k.

Given Total annual savings of Amit and Bharat = 1,32,000.

$\Rightarrow$ Total  monthly  savings = 11,000.

$\Rightarrow$ 55k = 11000

$\Rightarrow$ k = 200.

Hence monthly savings of Amit and Bharat are 7400 and 3600 respectively.

From the given data,

Let the monthly incomes of Amit and Bharat be 5x and 4x respectively, where ‘x’ is a constant.

Similalrly, let the monthly expenditures of Amit and Bharat be 19y and 21y respectively, where ‘y’ is a constant.

Savings =  Income – Expenditure

$\Rightarrow$ 5x – 19y = 7400……………………..(1)

and  4x – 21y = 3600………………………….(2)

Solving both the equations we get x = 3000 and y = 400.

Therefore, the monthly income of Amit is 5x i.e., 15000.

20) Answer (B)

According to BODMAS,

first Multiply the given numbers

0.3 x0.3= 0.09

0.03 x0.03=0.0009

0.6 x 0.03=0.018

simplifying this according to the given question,

0.09-0.0009-0.018=0.0729

now $\ \frac{\ 0.0729}{0.54}$

=> 0.135

Therefore answer is option b

21) Answer (D)

Prime factorization of :

$2400=(2)^5\times(3)\times(5)^2$

Now, to make it a perfect cube, we need to make the powers multiple of 3, and thus we need to divide it by = $(2)^2\times3\times(5)^2=300$

=> Ans – (D)

22) Answer (C)

From the figure, we can see that the distance walked by the man = HF.
AD = $10\sqrt3$
AH = $2\sqrt3$
HD = $8\sqrt3$
GD = $10/\sqrt3$
GF = $2/\sqrt3$
FD = $8/\sqrt3$
Therefore, HF = HD – FD = $8\sqrt3$ – $8/\sqrt3$ = $16/\sqrt3$

23) Answer (C)

For the first meeting, they have to cover 450 m by their relative speed.
The distance covered between 1st and 2nd meeting = Length of circular track = 900 m
So total distance that is to be covered = 900 +450 = 1350 m
Relative speed when they run in opposite direction = 30 + 45 = 75 m/s
Hence time taken in 1st meeting when they run in opposite direction($T_{2}$) = $\frac{1350}{75}$ = 18 seconds

Relative speed when they run in same direction = 30 – 45 = 15 m/s
Time taken in 1st meeting when they run in same direction($T_{1}$) = $\frac{1350}{15}$ = 90 seconds

Hence ratio of time taken till 2nd meeting in the same direction to opposite direction = $T_{1}$:$T_{2}$ = 5 : 1 (Answer :C)

24) Answer (D)

Taking the vowels (EA) as one letter, the given word has the letters XTR (EA), i.e., 4 letters.

These letters can be arranged in $4! = 24$ ways

The letters EA may be arranged amongst themselves in $2!=2$ ways.

Number of arrangements having vowels together = $(24 \times 2) = 48$ ways

Total arrangements of all letters = $5!=120$ ways

=> Number of arrangements not having vowels together = $(120 – 48) = 72$ ways

=> Ans – (D)

25) Answer (C)

In a triangle, the angular bisector divides the side which it intersects in the ratio of other two sides.

So, In the triangle ABC, the angular bisector AD divides the side BC in the ration of AB and AC

$\Rightarrow$ BD : DC = AB : AC

Given BC = 10 cm and DC = 6 cm

$\Rightarrow$ BD = BC – DC = 10 – 6 = 4 cm

Then $AB =\frac{BD}{DC}\times AC = \frac{4}{6}\times 4.2 = 2\times 1.4 = 2.8$ cm

26) Answer (C)

Curved surface area of cylindrical pillar is given as A = 2$\pi$rh, where ‘r’ is base radius and ‘h’ is height of the cylinder.

So curved surface area of each pillar A = $2\times \pi\times 0.35\times 5 = 11 m^2$

Given there are 30 cylindrical pillars.

The curved surface area of half the number of pillars = 15 * A = 165 $m^2$.

Given rate of painting is Rs. 10 per $m^2$

The cost of painting curved surface of half the number of pillars = Curved surface area * rate of painting

= $165\times 10$

= Rs. 1650.

27) Answer (C)

Probability = Expected number of outcomes/ Total number of outcomes.

Total number of outcomes =  The number of ways of selecting 3 professors at random from a total of 10 professors.

= 10C3 = 120 ways.

Expected number of outcomes = Selecting 3 professors so that at least one of the junior professor is selected.

The possible cases are,

Case(1): Selecting 1 junior professor out of 4 and Selecting 2 senior professor out of 6 = 4C1 * 6C2.

Case(2): Selecting 2 junior professor out of 4 and Selecting 1 senior professor out of 6 = 4C2 * 6C1.

Case (3): Selecting 3 junior professor out of 4  = 4C3.

So Expected number of outcomes = 4C1 * 6C2 + 4C2 * 6C1 + 4C3 = $4\times 15 + 6\times 6 + 4$ = 100 ways.

Probability = $\frac{100}{120} = \frac{5}{6}$

28) Answer (C)

f(x)f($\frac{1}{x}$)= f(x)+f($\frac{1}{x}$)

For the above equation f(x)= 1+$x^n$ or 1-$x^n$

f(1) = 2 = 1+$1^3$

f(2) = 1+$2^3$

f(5) = 1+$5^3$ = 126

29) Answer (A)

a= only maths

b=only logical reasoning

c= only English

d = only maths and logical reasoning

e= only maths and English

f= only Logical Reasoning and English

g= all three

a+b+c+d+e+f+g = 850

d+g = 550

c+e+f+g=600

d+e+f = 350

30) Answer (C)

As can be seen from the above venn diagram distribution

Number of households reading only one newspaper = 22 + 26 + 16 = 64.

Hence, option C.

31) Answer (C)

Anuj takes 1 day to complete
Bharat takes 2 days
Chetan takes 4 days and Dhiraj takes 8 days to complete
option A chetan and Dhiraj together will take $\frac{4\times\ 8}{4+8}=\frac{32}{12}=\frac{8}{3\ }days$so A is correct.
Now calculating for all we get AB in 2/3 days AC in 4/5 days AD in 8/9 days BC in 8/6 days BD in 16/10 days
So we can say BD is 2nd slowest pair
Hence A and C are correct

32) Answer (C)

543 in base 6 expressed in decimal form =5(36)+4(6)+3 =207
317 in base 8 expressed in decimal form = 3(64)+8+7 =207
So statement 1 is correct
Now 16 in base 2 = 10000
32 in base 2 = 100000
Therefore statement 2 is false
Hence C is the correct answer

33) Answer (C)

Let the number of units of work to be done to fill an empty tank or empty a full tank be 12 units.
Work done by type 1 tap in 1 hour = 12/4 = 3 units
Work done by type 2 tap in 1 hour = -12/3 = -4 units (negative sign since type 2 tap drains the tank)
Let the number of type 1 taps be ‘n’.
So, number of type 2 taps = 10-n
So, overall work = 3n – 4*(10-n) = 3n – 40 + 4n = 7n – 40
Overall work done in 6 hours = (7n – 40) * 6 = 42n – 240

This is equal to 12. So, 42n – 240 = 12
=> n = 252/42 = 6

So, number of type-1 taps in the group = 6

34) Answer (C)

Given, Rajesh can check the quality of 1000 items in 5 hours

$\Rightarrow$ Efficiency of Rajesh = 200 items/hr.

Also given, Rakesh can complete the 75% of same job in 3 hours

$\Rightarrow$ time taken by Rakesh to complete 100% of the job = $\frac{100}{75}\times 3$ = 4 hours.

$\Rightarrow$ Efficiency of Rakesh = 250 items/hr.

Given in the process of checking 1300 items, Rakesh spends only 2 hours. Let say time spent by Rajesh be ‘t’ hours, which is also the total time taken.

Total Work = Efficiency $\times$ time taken

$\Rightarrow 1300 = 250\times 2 + 200\times t$

$\Rightarrow 200t = 800$

$\Rightarrow t = 4$

Hence the time taken in the process of checking 1300 items is 4 hours.

35) Answer (B)

Let a = students who attended only MA

b= students who attended only MSW

c= students who attended both

a+c= 35

b+c = 47

c= 12

=> a=23 and b= 35

Total = a+b+c = 23 + 35 + 12 = 70

36) Answer (B)

Let the number of pens sold be n.
So, total cost price = 20n
Profit = 10%
So, total selling price = (110/100) * 20n = 22n
So, 3 + 5 + 7 + … (n terms) = 22n
=> (n/2)*(2*3 + (n-1)*2) = 22n
=> (1/2)*(2*3 + (n-1)*2) = 22
=> 3 + n – 1 = 22
=> n = 22 – 2 = 20

37) Answer (C)

N = $2^8\times\ 9^2\times\ 5^3$

N = $2^8\times\ 3^4\times\ 5^3$

= $25\left(2^8\times\ 3^{ 4}\times\ 5\right)$

Number of factors = 9*5*2 = 90

C is the correct answer.

38) Answer (B)

Given, speed of a boat in still water (V) =  5 km/hr

Let speed of the stream be V’ km/hr.

time taken to go 20km downstream (t) = distance travelled$\div$relative speed of the boat

= $\frac{20}{V + V’}$

=$\frac{20}{5 + V’}$ hours

time taken to go 20 km upstream (t’) =  distance travelled$\div$relative speed of the boat

= $\frac{20}{V – V’}$

= $\frac{20}{5 – V’}$ hours

Given that t’ = 3*t

$\Rightarrow \frac{20}{5 – V’} = 3\times \frac{20}{5 + V’}$

$\Rightarrow 4V’ = 10$

$\Rightarrow V’ = 2.5$ km/hr.

So the speed of the stream is 2.5 km/hr.

39) Answer (C)

We have to find the range of the expression. Let $\frac{x}{x^2 – 3x + 4}$ = y
So, $x = y*x^2 – 3xy + 4y$
=> $y * x^2 + x*(-3y – 1) + 4y = 0$
Since ‘x’ is real, the discriminant has to be greater than or equal to 0.
So, $(-3y-1)^2 – 4*y*4y \geq 0$
=> $7y^2 – 6y -1 \leq 0$
=> -1/7 $\leq y \leq$ 1
So, the maximum value of $\frac{x}{x^2 – 3x + 4}$ is 1 and the minimum value is -1/7

40) Answer (A)

$sin A$ = $\dfrac{1}{4 cosA}$
=> $sin A cos A = \frac{1}{4}$
$2 sin A cos A = \frac{1}{2}$
$ sin 2A = \frac{1}{2}$
$=> 2A = 30^{\circ}$
$A = 15^{\circ}$
$4A = 60^{\circ}$
$tan 60^{\circ} = \sqrt{3}$
Therefore, option A is the right answer.

41) Answer (C)

Let the number of students who play all the three sports be ‘c’. Number of students who play exactly two sports = b
Number of students who play exactly one sport = a
So, a + b + c = 200
a + 2b + 3c = 60 + 80 + 120 = 260
So, b + 2c = 60
c = 20
So, b = 60 – 40 = 20
So, the number of students who play at least two sports = b + c = 20 + 20 = 40

42) Answer (D)

Let the number of people who read all three magazines be ‘c’. The number of people who read exactly two magazines be ‘b’ and the number of people who read exactly one magazine be ‘a’.
a+b+c = 80
a+2b+3c = 20 + 40 + 33 = 93
To find the minimum number of people who read all the three magazines, we have to minimize ‘c’.
From the above two equations, we get, b + 2c = 13
If b = 13, c = 0. The value of ‘a’ in this case is 80 – 13 = 67
So, the minimum number of people who read all the three magazines is 0.

43) Answer (D)

let the length of the halls be ‘a’ and ‘a+1’ m respectively and height of the halls be ‘h’ m.

Area of 4 walls of first square hall (A1) = $(4\times a\times h) m^2$

Given, cost of painting is Rs. 5 per sq.m

$\Rightarrow$  cost of painting 4 walls of the first square hall = A1 * 5 = $4\times a\times h\times 5 = Rs. 20*a*h$.

Given that this cost of painting = Rs. 6000

$\Rightarrow$ 20*a*h = 6000………..(1)

Similarly,

Area of 4 walls of second square hall (A2) = $(4\times a+1\times h) m^2$

$\Rightarrow$  cost of painting 4 walls of the second square hall = A2 * 5 = $4\times a+1\times h\times 5 = Rs. 20*(a+1)*h$.

Given that this cost of painting = Rs. 6100

$\Rightarrow$ 20*(a+1)*h = 6100…………(2)

Dividing (2) with (1), we get

$\frac{a+1}{a} = \frac{6100}{6000}$

$\Rightarrow 1 + \frac{1}{a} = \frac{61}{60}$

$\Rightarrow a = 60$

Substituting this value in equation (1), we get

20*60*h = 6000

$\Rightarrow$ h = 5 m.

So, the height of the two walls is 5 m.

44) Answer (A)

The chord connecting 1 and 11 hour hand points makes 60 degrees because angle between consecutive hour hands is 30 degrees each. In a clock there are a total of 360 degree angle in the entirety of 12 hour hands.

Between 11 and 1 this will be equal to 60 degrees subtended at the centre O.

The distance between the hand point of 11 and 1 hour hands to the centre will be equal as they are symmetric points to the line joining 12 to the centre O.Let the point marked with 11 be A and 1 be B.

Since AOB is 60 degrees and sum of angles of a triangle is 180 degrees.

The AOB + ABO+ BAO = 180 degrees.

Since AO = BO.

ABO = BAO = 60 degrees

Let the point at 6 hour hand be C.

The angle subtended by a chord at circumference is half the angle subtended at the centre.

Hence ACB = 30 degrees.

The AB are symmetric about the the point C.

Hence CAB = CBA .

Since ACB = 30 degrees and ABC forms a triangle.

CAB + CBA = 150 degrees.

CAB = CBA = 75 degrees.

ACB = 30 degrees

45) Answer (C)

Let us consider the fucntion f(x) = $a\cos x + b\sin x + c$

The range of f(x) if given as $c – \sqrt{a^2 + b^2} \leq f(x) \leq c + \sqrt{a^2 + b^2}$

Then the maximum value of  3 $cosx+4 sinx+8$  is = 8 + $\sqrt{3^2 + 4^2}$

= 8 + 5 = 13

46) Answer (D)

we have : 2435753228
Now here we have 5 odd digits and 5 even digits and total 10 places
so 5,5,3,3,7 will arrange in 5 places and 2,2,2,8,4 will arrange in 5 places
we get : total arrangements =$\frac{5!}{3!}\times\ \frac{5!}{2!\times\ 2!}$
we get  $\frac{\left(5!\right)^2}{3!\ \left(2!\right)^2}$

47) Answer (C)

If the difference between any two dates is multiple of 7, then those two fall on same day of the week in any given month. Thus, 13 and 27 fall on same day.

=> Ans – (C)

48) Answer (B)

Vijay borrows at 8% p.a simple interest. Therefore, Vijay has to pay (10000*8*2)/100 = Rs. 1600 as interest for 2 years.

Rajnish borrows Rs.5000 at 10% p.a SI. Therefore, Rajnish has to pay (5000*10*2)/100 = Rs.1000 as interest for 2 years.

Kamal borrows at 10% p.a compound interest. Kamal has to pay $5000*(1.1)^2 -5000$ = Rs. 1050 as interest.

Therefore, Vijay will make a profit of 1050 + 1000 – 1600 = Rs. 450.

Therefore, option B is the right answer.

49) Answer (C)

Let the number of men be ‘m’ and number of women be ‘w’ in the class.

Given Average score of men = 70

$\Rightarrow$ Total score of men$\div$number of men = 70

$\Rightarrow$ Total score of men = 70$\times$m

Also, Average score of women = 83

$\Rightarrow$ Total score of women$\div$number of women = 83

$\Rightarrow$ Total score of women = 83$\times$w

Given the class average = 76

$\Rightarrow$ (Total score of men + Total score of women)$\div$(number of men + number of women) = 76

$\Rightarrow \frac{70\times m + 83\times w}{m + w} = 76 $

Let the ratio of number of men to women $\frac{m}{w} = k$

$\Rightarrow$ 70k + 83 = 76k + 76

$\Rightarrow$ 6k = 7

$\Rightarrow$ k = 7 : 6.

Hence the ratio of men to women in the class is 7 : 6.

50) Answer (D)

Given Speed of surya = 25 km/hr = $25\times \frac{5}{18} = \frac{125}{18}$ m/s.

Time taken(T) = Distance Travelled/ Speed

$\Rightarrow T =\frac{500}{\frac{125}{18}} = 72$ sec

Hence the time taken by Mr. Surya is ’72 sec’ or ‘1.2 min’.

51) Answer (A)

Probability of brother’s selection = $\frac{1}{8}$ and probability of brother’s rejection = $\frac{7}{8}$

Probability of sister’s selection = $\frac{1}{5}$ and probability of sister’s rejection = $\frac{4}{5}$

Probability that only one of them is selected = (prob. that brother is selected) × (prob. that sister is not selected) + (Prob. that brother is not selected) × (Prob. that sister is selected)

= $(\frac{1}{8})(\frac{4}{5})+(\frac{7}{8})(\frac{1}{5})$

= $\frac{4}{40}+\frac{7}{40}=\frac{11}{40}$

=> Ans – (A)

52) Answer (B)

In a triangle, the sum of two sides is always greater than the third side.

In the last two options, sum of first two sides is less than third side, and in first two options sum is equal to third side, hence these three are not possible.

Thus, possible lengths of triangle = [5,7,9]

=> Ans – (B)

53) Answer (D)

Let the two numbers be a-d and a+d such that their AM is ‘a’ and their GM is $\sqrt{a^2-d^2}$
Now the ratio of the squares of their GM and AM will be 9/25
=> ($a^2$-$d^2$)/$a^2$ = 9/25 or d = 4a/5
=> The numbers a-d, a+d can be written as a/5 and 9a/5
Thus, the numbers are in the ratio a/5 : 9a/5 or 1:9

54) Answer (B)

Given f(x) = $x^3 – 4x + p$ and  f(0) and f(1) are of opposite signs.

$\Rightarrow f(0)\times f(1) < 0$

$f(0) = 0^3 – 4*0 + p = p$

$f(1) = 1^3 – 4*1 + p = p-3$

$\Rightarrow (p)(p-3) < 0$

$\Rightarrow 0 < p < 3$.

55) Answer (C)

Let the cost of each orange, banana and apple be Rs. ‘o’ , ‘b’ , and ‘a’ respectively.

Given, Two oranges, three bananas and four apples cost Rs. 15

$\Rightarrow$ 2o + 3b + 4a = 15……….(1)

Also given, Three oranges, two bananas and one apple cost Rs. 10

$\Rightarrow$ 3o + 2b + a = 10…………(2)

Adding (1) and (2), we get,

5o + 5b + 5a = 25

$\Rightarrow$ o + b + a = 5

Then the cost of three oranges, three bananas and three apples is given as

3o + 3b + 3a = 3 [o + b + a] = 3$\times$ 5 = Rs. 15

56) Answer (B)

Sum of ages of A, B, C and D five years ago = $45\times4=180$

Sum of their present ages = $180+(5\times4)=200$

Sum of present ages of all five (including X) = $49\times5=245$

=> Present age of X = $245-200=45$ years

=> Ans – (B)

57) Answer (D)

$3^{85}$ and 51 have a common factor 3 => Euler’s theorem cannot be used here.
On cancelling 3, $3^{84}$ and 17 have no common factor => Euler’s theorem can be used.
Euler’s Totient of 17 = 16
=> $3^{16} (mod\ 17)$ = 1
=> $3^{80} (mod\ 17)$ = 1
$3^{84}(mod\ 17)$ = $3^{80}(mod\ 17)$ * $3^4(mod\ 17)$
$3^{84}(mod\ 17)$ = 1 * 13
=> $3^{85}(mod\ 17)$ = 13 * 3 = 39

58) Answer (A)

Let the present age of Ram be 6x and that of Shyam be 7x.
So $\frac{6x-14}{7x-14} = \frac{4}{5}$
=> 30x – 70 = 28x – 56
=> 2x = 14 => x =7
Thus the present ages of the two are 42 and 49 respectively.
20 years from now, the ratio of ages of the two will be 63 and 70 respectively.
So the required ratio will be 9:10

59) Answer (D)

Let the two numbers be $x$ and $4x$

=> $x\times4x=84\times21$

=> $x^2=(21)^2$

=> $x=21$

$\therefore$ Larger number = $4\times21=84$

=> Ans – (D)

60) Answer (D)

Interest of 1 year = 920-880=Rs.40

Since, Principal = Amount – Interest

=> Principal (before 2 years) = $880-40\times2=Rs.$ $800$

=> Ans – (D)

61) Answer (D)

$y^2 + 3y – 18 \geq 0$

$\Rightarrow y^2 + 6y – 3y – 18 \geq 0$

$\Rightarrow y (y+6) – 3 (y+6) \geq 0$

$\Rightarrow (y-3) (y+6) \geq 0$

$\Rightarrow y\geq3  and  y\leq-6$

62) Answer (C)

Time taken by machines A, B and C respectively is 2,3 and 6 hours

=> Time taken by all working together = $\frac{1}{2}+\frac{1}{3}+\frac{1}{6}$

= $\frac{6}{6}=1$ hour

=> Ans – (C)

63) Answer (D)

Let the total volume of the tank be 120 litres. Therefore, the inlet pipes fill 30, 20 and 15 litres/ hour respectively. The outlet pipes empty 60 and 12 litres/hour respectively. Therefore, the rate of outflow is more than the rate of inflow. Hence the tank can never be full.

64) Answer (A)

Let the capacity of the cistern be 600 units.

From the given data, the efficiencies of pipes A and B are 5 units/ min and 4 units/min respectively.

Let the efficiency of outlet pipe C be ‘k’ units/min.

Given the time taken to fill the cistern when all the three pipes are open = 100 minutes

$\Rightarrow Efficiency  of  pipes\times time  taken = Capacity  of  cistern$.

$\Rightarrow (5+4-k)\times 100 = 600$

$\Rightarrow 9-k = 6$

$\Rightarrow k = 3$

Therefore the time taken(t)  by pipe C to empty the cistern = $Capacity  of  the  cistern\div efficiency  of  pipe  C$

$\Rightarrow t = 600\div 3 = 200 minutes = 3 hrs 20 min$.

65) Answer (D)

The figure will be as shown below.

The area covered by the two circles = Sum of the areas of the two circles – Area of the region overlapped by the two circles
Area of each of the circle = $\pi\times r^2=4\pi$
Area of the segment enclosed by the line CD and the arc CD = Area of sector ACD – Area of triangle ACD = $\pi-2$
Area common to the two circles is $2\times (\pi – 2)$.
So, total area covered by the two circles is $4\pi + 4\pi – (2\pi – 4) = 6\pi + 4$

66) Answer (B)

The hands of a clock coincide 11 times in every 12 hours (Since between 11 and 1, they coincide only once, i.e., at 12 o’clock). The hands overlap about every 65 minutes, not every 60 minutes. Thus the minute hand and the hour hand coincide 22 times in a day.

Thus, the hands of a clock overlap 22 times a day. Thus the hands of the clock overlap at 12:00, ~1:05, ~2:10, ~3:15, ~4:20, ~5:25, ~6:30, ~7:35, ~8:40, ~9:45, ~10:50. Note that there is no ~11:55. This becomes 12:00.

=> Ans – (B)

67) Answer: 59

Total weight of the 10 students in the class = 545 kg
Average weight of the class after the student weighing 82 kg joined =$\frac{545+82}{11} = 57$kg
The average weight of the class after the 2nd student joined will be an integer only if the weight of the second student is 93 kg. This is because (545 + 82 + weight of the 2nd student) must be a multiple of 12.
Following the same logic, the weights of the 3rd, 4th and 5th student must be 60, 46 and 89 kg respectively.
Average weight of the class after the 4th student joined =$\frac{545+82+93+60+46}{14} = 59$ kg
Hence, option (4) is the correct choice

68) Answer (C)

We need to find the least n such that, 1+2+3+. . . +n >150.
So, n=17 and the alphabet is q

69) Answer (B)

From 32 litres, 4 litres is drawn out and is replaced with water.

Proportion of wine drawn = 4/32 = 1/8th of the total volume of the wine in the mixture.

When wine is drawn out for the second time, $(1/8)\times (28) = 3.5$ litres of wine will be drawn out.

Wine remaining in the jar = 28-3.5 = 24.5 litres

When wine is drawn out for the third time, $(1/8)\times (24.5) =3.0625$ litres of wine will be drawn out.

Wine remaining in the jar = 24.5 – 3.0625 = 21.4375 litres

Water in the jar = 10.5625 litres

Ratio of wine remaining in the jar to water remaining in the jar = 343:169

70) Answer (D)

In $\triangle$AOB, AO = OB (Equal radii)

∴ $\triangle$AOB is isosceles.

∴ ∠ABO = ∠BAO = (180°-114°)/2 = 33°

Hence, option D.

71) Answer (D)

Principal sum to be borrower = Rs. 25,000

Amount when compounded annually = $P(1+\frac{R}{100})^T$

=> Amount to be paid after 3 years = $25,000(1+\frac{3}{100})$ $(1+\frac{4}{100})$ $(1+\frac{5}{100})$

= $250\times103\times\frac{26}{25}\times\frac{21}{20}$

= $103\times13\times21=Rs.$ $28,119$

=> Ans – (D)

72) Answer (C)

Let speed of Raj be v1 and speed of Rahul be v2
Now Rahul reaches 5 seconds before Raj and beats him by 50m
so Raj covers 50m in 5 seconds
so v1 = 10m/s
Now When Raj covers 950m Rahul covers 1000m (in the same time )
so we get $\frac{v1}{v2}=\frac{1000}{950}$
v1 =$\frac{200}{19}\ =10\ \frac{10}{19}\ $ m/sec

73) Answer (C)

Expression : $(y^2 – 5y + 5)^{(y – 8)(y + 6)} = 1$

=> $log(y^2 – 5y + 5)^{(y – 8)(y + 6)} = log(1)$

=> $(y-8)(y+6)log(y^2-5y+y)=0$

Thus, either $(y-8)=0$ or $(y+6)=0$ or $log(y^2-5y+5)=0$

=> $y=8,-6$ —————(i)

or $log(y^2-5y+5)=log(1)$

=> $y^2-5y+4=0$

=> $(y-4)(y-1)-0$

=> $y=4,1$ ———–(ii)

From equations (i) and (ii), Possible values of $y$ (natural number) = 3

=> Ans – (C)

74) Answer (B)

Whenever some cubes are melted to form a single larger cube, the total volume always remains constant.

So, Sum of the volumes of three small cubes = Volume of the larger cube.

Let the side of the lager cube so formed be ‘a’ cm.

Then $1^3 + 6^3 + 8^3 = a^3$

$\Rightarrow a^3 = 729$

$\Rightarrow a = 9$ cm.

Surface area of cube so formed = 6*$a^2$ = $6\times 9^2 = 6\times 81 = 486  cm^2$

75) Answer (B)

Let the father’s age be 10x+y and the daughter’s age be 10y+x

Difference between their ages is more than 10 years. So the eqn is:

(10x+y)-(10y+x)>10

=> 9(x-y)>10

=> (x-y)>1.11    …(1)

Also sum of their ages is 55.

(10x+y)+(10y+x)=55

=>11(x+y)=55

=> x+y = 5    …(2)

Solving (1) and (2) together, we get x=4 and y=1

So, daughter’s age is 14.

76) Answer (D)

Let $x=2$ and $y=3$

To find : $\frac{3x+2y}{2x+5y}$

= $\frac{3(2)+2(3)}{2(2)+5(3)}$

= $\frac{12}{19}$

=> Ans – (D)

77) Answer (A)

Let x = -2, y = 1 and n = 2, then x^n > y^n, but x < y, so option b) is not true
Let x = -2, y = 1, then $x^2$ > $y^2$ but $x^3 < y^3$. So, option c) is not true
Option a) is true. If ‘n’ is an odd number and $x^n > y^n$, then it is necessarily true that x > y.

78) Answer (D)

Let the time for which the investment was made be ‘n’ years.
So, compound interest = $5000*(1+5/100)^n – 5000 = 788$
=> $5000(21/20)^n = 5788$
n = 3 satisfies the equation
So, the amount was borrowed for a period of 3 years

79) Answer (D)

Probability of A or B = Probability of A + Probability of B – Probability of A and B.

$\Rightarrow$ Probability of drawing king or heart = Probability of drawing king + Probability of drawing heart – Probability of drawing kings which are hearts from the deck of cards.

A deck of cards contain 52 cards, of which there are 4 kings and 13 hearts and 1 king which is heart also.

Probability of drawing a king = $\frac{4}{52}$

Probability of drawing a heart = $\frac{13}{52}$

Probability of drawing a king which are heart also = $\frac{1}{52}$

$\Rightarrow$ Probability of drawing king or heart = $\frac{4}{52} + \frac{13}{52} – \frac{1}{52}$

= $\frac{16}{52}$

= $\frac{4}{13}$

80) Answer (C)

Children who like only chocolate ice cream = 6

Children who like only butter scotch ice cream = 5

Children who like both chocolate and butter scotch = 5

The given data can be represented in the Venn diagram as shown below

$\therefore\ $Total number of ice creams to be ordered = 6 + 5 + 5 = 16

Hence, the correct answer is Option C

81) Answer (B)

Let the number be ‘x’

one-fourth of the number = $\frac{1}{4}\times x = \frac{x}{4}$

one-third of one-fourth of the number = $\frac{1}{3}\times \frac{x}{4} = \frac{x}{12}$

Given, one-third of one-fourth of the number is = 15

$\Rightarrow \frac{x}{12} = 15$

$\Rightarrow x = 180$

Hence the number is 180.

Then three-tenth of the number = $\frac{3}{10}\times x = \frac{3}{10}\times 180 = 54$

82) Answer (D)

we have :

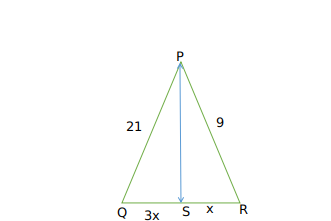
Triangles PSR and PSQ are right triangles
so using pythaghoras theorem
we get
441 = $PS^2+9x^2$
81 =$PS^2+x^2$
subtracting we get
360=$8x^2$
$x^2\ =45$
x=$3\sqrt{\ 5}$
QR = 4x = $12\sqrt{\ 5}$

83) Answer (B)

Value of first machine at the end of two years = 0.9*0.9*1500 = 1215
Value of the second machine at the end of two years = 0.85*0.85*1000 = 722.5
Depreciated value = 2500 – 1215 – 722.50=562.5

84) Answer (D)

Let length and breadth of field be $l$ and $b$ km

Perimeter = $2(l+b)=18$

=> $l+b=9$ —————-(i)

Area = $lb=20$ ————(ii)

Substituting value from equation (i), we get : $l(9-l)=20$

=> $l^2-9l+20=0$

=> $(l-5)(l-4)=0$

=> $l=5,4$

$\therefore$ Length of longest side = 5 km

=> Ans – (D)

85) Answer (D)

Let Steve’s salary = $Rs.$ $10$

=> John’s salary = $\frac{80}{100}\times10=Rs.$ $8$

=> Tom’s salary = $\frac{150}{100}\times8=Rs.$ $12$

$\therefore$ Ratio of Steve’s salary to Tom’s salary = $\frac{10}{12}=5:6$

=> Ans – (D)

86) Answer (A)

Principal amount = Rs. 1400, time period = 9 months and interest = Rs. 21

Simple interest = $\frac{P\times R\times T}{100}$

=> $\frac{1400\times r\times9}{12\times100}=21$

=> $r=\frac{21\times12}{126}=2%$

=> Ans – (A)

87) Answer (C)

$cotA = \frac{1}{tanA}$

let $tanA = x, then  cotA = \frac{1}{x}$

Given, x + $\frac{1}{x} = \sqrt 5$………………………..(1)

Cubing on both sides, we get

$(x + \frac{1}{x})^3 = \sqrt 5^3$

$\Rightarrow x^3 + \frac{1}{x}^3 + 3\times x\times \frac{1}{x}\times (x + \frac{1}{x}) = 5\sqrt 5$

$\Rightarrow x^3 + \frac{1}{x}^3 + 3\times \sqrt 5 = 5\sqrt 5$

$\Rightarrow x^3 + \frac{1}{x}^3 = 2\sqrt 5$.

$\Rightarrow tanA^3 + cotA^3 = 2\sqrt 5$.

88) Answer (B)

The length of each rope is half the diagonal of the square = 10/1.414 = 7.07.
The area grazed by each sheep is equal to one-fourth of the circle formed with center at the vertex of the square and radius equal to half the diagonal of the square.
So the total area grazed is equal to $((1/2)*3.14*7.07^{2}) = 78.53 $ sq m

89) Answer (A)

60 minutes = 360 degrees or 2$\pi$ radians.

$\Rightarrow$ 1 minute = 60  degrees.

$\Rightarrow$ 30 minutes = 180  degrees  or  $\pi$ radians.

Therefore area (A) swept by minute hand of length 42 mm in 30 minutes =  area of semi-circle of radius (r = 42 mm) .

$\Rightarrow A = \pi r^2\div 2 = 3.14\times 42^2\div 2 = 2769.5 mm^2$.

 

90) Answer (D)

According to ques,

=> $(\frac{65}{100}\times X)-(\frac{36}{100}\times X)=2900$

=> $\frac{29X}{100}=2900$

=> $X=10000$

$\therefore$ 122% of X = $\frac{122}{100}\times10000=12200$

=> Ans – (D)

91) Answer (C)

Since balls of same color should come together, let us consider 3 red balls as one unit and 2 blue balls as one unit and 4 yellow balls as another unit.

So, we have a total of 3 different units which can be arranged in ‘3!’ ways.

these 3 red balls can internally be arranged in ‘3!’ ways.

Similarly the blue balls and yellow balls can be arranged internally in ‘2!’ and ‘4!’ ways respectively.

So, total number ways = $3!\times 3!\times 2!\times 4!= 6\times 6\times 2\times 24$= 1728 ways

92) Answer (A)

A and B working together finish a work in 6 hours.

Time taken by A alone = 10 hours

=> Time taken by B alone = $\frac{1}{6}-\frac{1}{10}=\frac{4}{60}=\frac{1}{15}$

$\therefore$ B takes 15 hours to finish the work.

=> Ans – (A)

93) Answer (A)

Let quadratic equation be $x^2+bx+c\ =0$
Now Sarika made a mistake in reading b , so she would have read c correctly
so c/1 = product of roots =192   (1)
Meera made a mistake in reading the constant term of the equation so she would have read b correctly
now sum of roots = -b/1 =-28  (2)
we get b =28 , c =192
so quadratic becomes
$x^2+28x+192$
we get (x+16)(x+12) =0
roots are -16 , -12

94) Answer (D)

Given Anil is twice as good a student as Bharat

$\Rightarrow$ Efficiency  of  Anil : Efficiency  of  Bharat = 2:1

and also, Efficiency is inversely proportional to Time taken,

$\Rightarrow$ Time  taken  by  Anil : Time  taken  by  Bharat = 1:2………………………….(1)

Given that Time taken by Anil is 30 min less than Bharat’s time.

Let say, Time taken by Bharat be ‘t’ minutes.

Then the time taken by Anil = t-30 minutes

Substituting these in equation (1), we get

$\frac{t-30}{t} = \frac{1}{2}$

$\Rightarrow$ t = 60  minutes.

Therefore the time taken by Anil and Bharat are 30 minutes and 60 minutes respectively.

Let Efficiency of Bharat be ‘x’, then Efficiency of Anil will be ‘2x’

$\Rightarrow$ Total Work = Efficiency\times Time taken = $(2x)\times 30 (or) (x)\times 60 = 60x$  units.

Efficiency when Anil and Bharat are working together = x+2x = 3x

Total Work = 60x units

Time taken(T) by Anil and Bharat together to complete the work = Total work/ Efficiency when Anil and Bharat work together

$\Rightarrow T = \frac{60x}{3x}$

$\Rightarrow$ T = 20  minutes.

95) Answer (A)

Given log 625 = 2.796

4 log 5 = 2.796

log 25 = 2 log 5 = 1.398

96) Answer (A)

Given      0<a<1……………………………………….(1)

Let us go with the verification of options

Option (i):

squaring on both sides of (1), we get

0<$a^2$<1

Subtracting ‘1’ in the above equation, we get

-1<$a^2$-1<0………………..(2)

$\Rightarrow a^2$-1< 0, Hence option (i) is false.

Option (ii):

Squaring on both sides of (1), we get

0<$a^2$<1

Adding ‘1’ on both sides of above equation, we get

1<$a^2$+1<2………………..(3)

$\Rightarrow a^2$+1>0, Hence Option (ii) is true.

Option (iii):

As 0<a<1, $a^2<a$………….(4)

Subtracting ‘a’ on both sides of (4), we get

$a^2-a<0$, Hence Option (iii) is also false.

 

97) Answer (B)

Let say f(x) = $x^3 + 2x^2 + bx + 68$ and given (x+4) is a factor of f(x).

$\Rightarrow f(x) = (x+4)\times k$……………..(1)

where ‘k’ is the quotient when f(x) is divided by (x+4).

Substituting ‘x= -4’ in the equation (1), we get

f(-4) = 0

$\Rightarrow -4^3 + 2 (-4)^2 + b (-4) + 68 = 0$

$\Rightarrow -64 + 32 – 4b + 68 = 0$

$\Rightarrow 4b = 36$

$\Rightarrow b = 9$.

98) Answer (C)

The two frogs are at diametrically opposite ends, so when they go towards the worm at point B, it becomes a right angled triangle, as angle in a semi circle is right angle.

=> $\angle ABC=90^\circ$

=> Ans – (C)

99) Answer (B)

Let amount received by Amar, Akbar and Anthony = Rs. $2x,3x$ and $7x$ respectively

According to ques, => $2x+15=7x$

=> $x=\frac{15}{5}=3$

$\therefore$ Akbar’s share = $3\times3=Rs.$ $9$

=> Ans – (B)

100) Answer (C)

Given : ABC is an isosceles triangle, with AB=AC, let $\angle$ ABC $=\angle$ ACB = $x$

=> $\angle$ BAC = $8x$

Also, AD is angle bisector, => $\angle$ BAD $=\angle$ CAD = $4x$

The angle bisector of an isosceles triangle is perpendicular bisector to the base.

=> $\angle$ BDA $=\angle$ CDA = $90^\circ$

Thus, in right triangle ABD, => $\angle$ ABD + $\angle$ ADB + $\angle$ BAD = $180^\circ$

=> $x+4x=180-90=90^\circ$

=> $x=\frac{90}{5}=18^\circ$

$\therefore$ $\angle$ BAD = $4\times18=72^\circ$

=> Ans – (C)

Enroll to CAT 2022 Complete course

Download TISSNET Previous Papers PDF