TISSNET Linear Equations Questions [Download PDF]

Linear Equations are one of the most important topics in the TISSNET Quant section. To ace this topic, one must need to cover all the basics and fundamentals. It is advised to practice a good number of questions from the Linear Equations. Cracku provides you with some important TISSNET Linear Equations questions  PDF with detailed solutions. These questions were taken from the previous TISSNET papers, which are very imperative in TISSNET preparation. After solving these questions, one can gain much confidence to solve these types of questions in the actual TISSNET examination. Click on the link below to download the TISSNET Linear Equations Questions with detailed solutions PDF.

Download Linear Equations Questions for TISSNET

Get 5 TISSNET 2023 Mocks At just Rs. 299

Question 1: If a – b : b – c : c – d = 1 : 2 : 3, then what is the value of (a + d) : c?

a) 1 : 2

b) 2 : 1

c) 4 : 1

d) 3 : 1

1) Answer (B)

Solution:

Given = $(a-b):(b-c):(c-d)=1:2:3$

=> $\frac{a-b}{b-c}=\frac{1}{2}$

=> $2a-2b=b-c$

=> $2a+c=3b$ ———–(i)

Similarly, $\frac{b-c}{c-d}=\frac{2}{3}$

=> $3b-3c=2c-2d$

=> $3b=5c-2d$ ———-(ii)

Substituting above value in equation (i), we get :

=> $2a+c=5c-2d$

=> $2a+2d=5c-c$

=> $2(a+d)=4c$

=> $\frac{a+d}{c}=\frac{4}{2}=2$

$\therefore$ $(a+d):c=2:1$

=> Ans – (B)

Question 2: What is the value of $\frac{(0.7)^{3}-(0.4)^{3}}{(0.7)^{2}+\ 0.7\times0.4+(0.4)^{2}}\ $?

a) 0.3

b) 0.4

c) 0.7

d) 1.1

2) Answer (A)

Solution:

Expression = $\frac{(0.7)^{3}-(0.4)^{3}}{(0.7)^{2}+\ 0.7\times0.4+(0.4)^{2}}\ $

Let $x=0.7$ and $y=0.4$

= $\frac{x^3-y^3}{x^2+xy+y^2}$

= $\frac{(x-y)(x^2+xy+y^2)}{x^2+xy+y^2}$

= $x-y=0.7-0.4=0.3$

=> Ans – (A)

Question 3: What is the value of $3^{2}+7^{2}+13^{2}+17^{2}-1^{2}-5^{2}-9^{2}-11^{2}-15^{2}$?

a) 5

b) 72

c) 92

d) 63

3) Answer (D)

Solution:

Expression = $3^{2}+7^{2}+13^{2}+17^{2}-1^{2}-5^{2}-9^{2}-11^{2}-15^{2}$

= $(9+49+169+289)-(1+25+81+121+225)$

= $516-453=63$

=> Ans – (D)

Question 4: If P = (√7 – √6)/(√7 + √6), then what is the value of P + (1/P)?

a) 12

b) 13

c) 24

d) 26

4) Answer (D)

Solution:

Given : $P=\frac{\sqrt7-\sqrt6}{\sqrt7+\sqrt6}$ —————(i)

=> $\frac{1}{P}=\frac{\sqrt7+\sqrt6}{\sqrt7-\sqrt6}$ ———-(ii)

Adding equations (i) and (ii),

=> $P+\frac{1}{P}=(\frac{\sqrt7-\sqrt6}{\sqrt7+\sqrt6})+(\frac{\sqrt7+\sqrt6}{\sqrt7-\sqrt6})$

= $\frac{(\sqrt7-\sqrt6)^2+(\sqrt7+\sqrt6)^2}{(\sqrt7+\sqrt6)(\sqrt7-\sqrt6)}$

= $\frac{(13-2\sqrt{42})+(13+2\sqrt{42})}{7-6}$

= $13+13=26$

=> Ans – (D)

Question 5: $If\ \frac{cos\ \theta}{1+sin\ \theta}+ \frac{cos\ \theta}{1-sin\ \theta}=2\sqrt{2}\ and\ \theta\ $is acute, then what is the value (in degrees) of $\theta$?

a) 30

b) 45

c) 60

d) 90

5) Answer (B)

Solution:

Given,

$ \frac{cos\ \theta}{1+sin\ \theta}+ \frac{cos\ \theta}{1-sin\ \theta}=2\sqrt{2}\ $

$\cos\theta(\frac{1}{1+sin\ \theta}+ \frac{1}{1-sin\ \theta})=2\sqrt{2}\ $

$\cos\theta (\frac{1 – \sin\theta + 1 + \sin\theta}{1^{2} – \sin^{2}\theta}) = 2\sqrt{2}$

$\cos\theta (\frac{2}{\cos^{2}\theta}) = 2\sqrt{2}$

$\cos\theta = \frac{1}{\sqrt{2}}$

$\theta = 45^{\circ}$

Hence, option B is the correct answer.

Question 6: If cot $\theta=\sqrt{11}\ and\ \theta\ $is acute, then what is the value of $(\frac{cosec^{2}\ \theta\ +\ sec^{2}\ \theta}{cosec^{2}\ \theta\ -\ sec^{2}\ \theta})$?

a) 2/3

b) 6/5

c) 3/4

d) 7/6

6) Answer (B)

Solution:

Given, cot $\theta=\sqrt{11}$

$(\frac{cosec^{2}\ \theta\ +\ sec^{2}\ \theta}{cosec^{2}\ \theta\ -\ sec^{2}\ \theta})$ = $(\frac{1 + cot^{2}\ \theta\ +\ 1 + tan^{2}\ \theta}{1 + cot^{2}\ \theta\ -\ 1 + tan^{2}\ \theta})$

$\Rightarrow (\frac{1 + 11\ +\ 1 + \frac{1}{11}}{1 + 11\ -\ 1 + \frac{1}{11}})$ = $(\frac{\frac{144}{11}}{\frac{120}{11}})$ = $\frac{144}{20}$

$\Rightarrow \frac{6}{5}$

Hence, option B is the correct answer.

Question 7: If sin θ + $sin^{2}$ θ = 1, then what is the value of $(cos^{12}\ \theta\ + 3\ cos^{10}\ \theta+3\ cos^{8}\ \theta\ + cos^{6}\ \theta -1)$

a) -1

b) 0

c) 1

d) 2

7) Answer (B)

Solution:

Given $sin \theta + sin^{2} \theta = 1$

$\Rightarrow sin$ θ = 1 – $sin^{2}$ θ $\Rightarrow$ $sin$ θ = $cos^{2}$ θ …..(1)

Now, $(cos^{12}\ \theta\ + 3\ cos^{10}\ \theta+3\ cos^{8}\ \theta\ + cos^{6}\ \theta -1)$

$(cos^{4} \theta$ + $cos^{2} \theta)^{3}$ – 1

Substitute equation (1) in the above equation

$(sin^{2} \theta$ + $cos^{2} \theta)^{2}$ – 1

1 – 1 = 0

Hence, option B is the correct answer.

Question 8: If $(1+ tan^{2} \theta) = \frac{625}{49}\ and\ \theta\ $is acute, then what is the value of $\ (\sqrt{sin \theta+cos\ \theta})\ $?

a) 1

b) $\frac{5}{4}\sqrt{\frac{31}{42}}$

c) $\frac{\sqrt{31}}{5}$

d) 5/7

8) Answer (C)

Solution:

Given,

$(1+ tan^{2}\theta)$ = $\frac{625}{49}$   (or) $sec^{2}\theta$ = $\frac{625}{49}$

$sec\ \theta$ = $\frac{25}{7}$

$Cos\ \theta = \frac{7}{25}$ and $sin\ \theta = \frac{24}{25}$

$\ \sqrt{sin \theta+cos\ \theta}\ = \sqrt{\frac{7 + 24}{25}}$ = $\sqrt{\frac{31}{25}}$  =  $\frac{\sqrt{31}}{5}$

Hence, option C is the correct answer.

Question 9: If sec$\theta=\frac{13}{12}\ and\ \theta\ $is acute, then what is the value of $(\sqrt{cot\theta+tan \theta})$?

a) $\frac{13}{2\sqrt{15}}$

b) $\frac{12}{2\sqrt{13}}$

c) $\frac{13}{2\sqrt{5}}$

d) $\frac{2}{13}$

9) Answer (A)

Solution:

Given,

sec$\theta = \frac{13}{12}$

Then, cot$\ \theta = \frac{12}{5}$ and tan$\ \theta = \frac{5}{12}$

$(\sqrt{cot\theta+tan \theta})$ = $(\sqrt{\frac{12}{5}+\frac{5}{12}})$ =  $(\sqrt{\frac{169}{60}})$ = $\frac{13}{2\sqrt{15}}$

Hence, option A is the correct answer.

Question 10: In ΔPQR, ∠P : ∠Q : ∠R = 1 : 3 : 5. What is the value (in degrees) of ∠R – ∠P?

a) 30

b) 80

c) 45

d) 60

10) Answer (B)

Solution:

Let, ∠P = 1x, ∠Q = 3x, ∠R = 5x

Sum of interior angles of a triangle = 180 degrees i.e

∠P + ∠Q + ∠R = 180 degrees

$\Rightarrow$ 9x = 180 (or) x = 20

∠R – ∠P = 5x – 1x

∠R – ∠P = 4x (or) 4 x 20

∠R – ∠P = 80

Hence, option B is the correct answer.

Question 11: If x + y + z = 0, then what is the value of $\frac{x^{2}}{yz}+\frac{y^{2}}{xz}+\frac{z^{2}}{xy}$?

a) 0

b) 1/3

c) 1

d) 3

11) Answer (D)

Solution:

Given x + y + z = 0. So, x + y = -z, y + z = -x, z + x = -y ———–(1)

$\frac{x^{2}}{yz}+\frac{y^{2}}{xz}+\frac{z^{2}}{xy}$

$\frac{x^{3} + y^{3} + z^{3}}{xyz}$ ———–(2)

We know that, $a^{3} + b^{3} + c^{3} = (a+b+c)^{3} – 3ab(a+b) – 3bc(b+c) – 3ac(a+c) – 6abc$

Hence, equation (2) can be written as,

$\frac{(x+y+z)^{3} – 3xy(x+y) – 3yz(y+z) – 3zx(x+z) – 6xyz}{xyz}$

Now substitute equation (1) in the above equation,

$\frac{(0)^{3} + 3xy(z) + 3yz(x) + 3zx(y) – 6xyz}{xyz}$

$\frac{3xyz}{xyz}$ = 3

Hence, option D is the correct answer.

Question 12: If$\ x^{2}+\frac{1}{x^{2}}=\frac{7}{4}$ for x > 0, then what is the value of x + $\frac{1}{x}$?

a) 2If

b) √15/2

c) √5

d) √3

12) Answer (B)

Solution:

Let,

$(x + \frac{1}{x})^{2}$ = $\ x^{2}+\frac{1}{x^{2}} + 2(x)(\frac{1}{x})$

$(x + \frac{1}{x})^{2}$ = $\frac{7}{4} + 2$

$(x + \frac{1}{x})^{2}$ = $\frac{15}{4}$

$(x + \frac{1}{x})$ = $\frac{\sqrt{15}}{2}$

Hence, option B is the correct answer.

Question 13: If$\frac{1}{x+2}=\frac{3}{y+3}=\frac{1331}{z+1331}=\frac{1}{3}$, then what is the value of $\frac{x}{x+1}+\frac{4}{y+2}+\frac{z}{z+2662}?$

a) 0

b) 1

c) 3/2

d) 3

13) Answer (C)

Solution:

Given $\frac{1}{x+2}=\frac{1}{3}$

We get x = 1 …..(1)

$\frac{3}{y+3}=\frac{1}{3}$

we get y = 6 …..(2)

$\frac{1331}{z+1331}=\frac{1}{3}$

we get z = 2662 ….(3)

We need to find $\frac{x}{x+1}+\frac{3}{y+3}+\frac{z}{z+2662}$

Substitute equations (1), (2) and (3) in the above equation

= $\frac{1}{1+1}+\frac{3}{6+3}+\frac{2662}{2662+2662}$

= $\frac{1}{2}+\frac{3}{9}+\frac{1}{2}$

= $\frac{3}{2}$

Hence, option C is the correct answer.

Question 14: When a = 61, b = 63 and c = 65, then what is the value of a$^{3}$ + b$^{3}$ + c$^{3}$ – 3abc?

a) 1456

b) 2268

c) 4536

d) 5460

14) Answer (B)

Solution:

We know that $(a + b + c)^{3} – 3abc= \frac{1}{2}(a + b + c)((a – b)^{2} + (b – c)^{2} + (c – a)^{2})$

$\Rightarrow \frac{1}{2} (61 + 63 + 65)((61 – 63)^{2}$ + $(63 – 65)^{2}$ + $(65 – 61)^{2})$

$\Rightarrow \frac{1}{2} (189)(2^{2} + 2^{2} + 4^{2})$ = $ \frac{1}{2} (189)(24) = 2268$

Hence, option B is the correct answer.

Instructions

The bar graph given below represents the revenue of a firm for 8 years. All the revenue figures have been shown in terms of Rs crores.

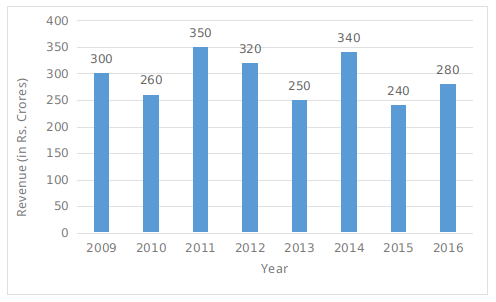
Question 15: What is the total value of revenue of the firm (in crores Rs) in years 2010, 2011 and 2012?

a) 910

b) 930

c) 950

d) 1020

15) Answer (B)

Solution:

Total value of revenue of the firm in years 2010, 2011 and 2012 = 260 + 350 + 320 = 930

Hence, option B is the correct answer.

Question 16: A certain sum becomes Rs 1020 in 5 years and Rs 1200 in 8 years at simple interest. What is the value of principal?

a) 820

b) 780

c) 700

d) 720

16) Answer (D)

Solution:

Simple interest for 3 years = 1200 – 1020 = 180 (or 60 for 1 year)

Then simple interest for 5 years = 300

Sum becomes 1020 in 5 years, hence, principal amount = 1020 – 300 = 720.

Hence, option D is the correct answer.

Question 17: The price of motorcycle depreciates every year by 8%. If the value of the motorcycle after 2 years will be Rs 84640, then what is the present value (in Rs) of the motorcycle?

a) 90000

b) 102000

c) 110000

d) 100000

17) Answer (D)

Solution:

Given that price of motorcycle depreciates every year by 8% then after 2 years,

92% of 92% of $x = 84,640$

$\frac{92}{100}$ x $\frac{92}{100}$ x $x = 84,640$

$x = 100000$

Hence, option D is the correct answer.

Question 18: P is 20% more than Q and 40% less than R. If value of Q is Rs 150, then what is the value of R (in Rs)?

a) 300

b) 320

c) 220

d) 250

18) Answer (A)

Solution:

Given P is 20% more than Q,

P = 120% of Q (or) P = (6/5) x 150 (Q = 150)

P = 180

P is 40% less than R,

P = 60% of R (or) 180 = (3/5) x R

R = 300

Hence, option A is the correct answer.

Question 19: If 2A = 3B, then what is the value of (A + B)/A?

a) 5/4

b) 2/3

c) 5/2

d) 5/3

19) Answer (D)

Solution:

Given, 2A = 3B i.e

$\frac{A}{B} = \frac{3}{2}$ (or) $\frac{B}{A} = \frac{2}{3}$

Now, $\frac{A+B}{A} \Rightarrow (\frac{A}{A} + \frac{B}{A}$) $\Rightarrow (1 + \frac{2}{3}) = \frac{5}{3}$

Hence, option D is the correct answer.

Question 20: What is the value of $\frac{(0.5^{3})-(0.1)^{3}}{(0.5)^{2}+0.5 \times 0.1+(0.1)^{2}}$?

a) 0.1

b) 0.4

c) 0.5

d) 0.6

20) Answer (B)

Solution:

Given $\frac{(0.5^{3})-(0.1)^{3}}{(0.5)^{2}+0.5 \times 0.1+(0.1)^{2}}$……(1)

we know that $a^{3} – b^{3} = (a – b) (a^{2} + ab + b^{2})$……(2)

Substitute (2) in (1)

$\frac{(0.5-0.1)(0.5)^{2} + 0.5 \times 0.1 + (0.1)^{2}}{(0.5)^{2}+0.5 \times 0.1+(0.1)^{2}}$

$0.5 – 0.1 = 0.4$

Hence, option B is the correct answer.

Get 5 TISSNET 2023 Mocks At just Rs. 299

Download MBA Preparation App