Tables DI Questions for NMAT PDF:

Download Tables DI Questions for NMAT PDF. Top 10 very important Tables DI Questions for NMAT based on asked questions in previous exam papers.

Download Tables DI Questions for NMAT

Get 5 NMAT Mocks for Rs. 499

Take NMAT mock test

Instructions

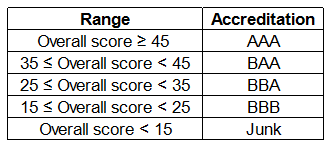
An agency entrusted to accredit colleges looks at four parameters: faculty quality (F), reputation (R), placement quality (P), and infrastructure (I). The four parameters are used to arrive at an overall score, which the agency uses to give an accreditation to the colleges. In each parameter, there are five possible letter grades given, each carrying certain points: A (50 points), B (40 points), C (30 points), D (20 points), and F (0 points). The overall score for a college is the weighted sum of the points scored in the four parameters. The weights of the parameters are 0.1, 0.2, 0.3 and 0.4 in some order, but the order is not disclosed. Accreditation is awarded based on the following scheme:

Eight colleges apply for accreditation, and receive the following grades in the four parameters (F, R, P, and I):

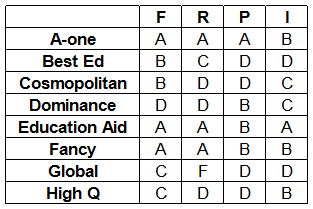
It is further known that in terms of overall scores:
1. High Q is better than Best Ed;
2. Best Ed is better than Cosmopolitan; and
3. Education Aid is better than A-one.

Question 1: What is the weight of the faculty quality parameter?

a) 0.2

b) 0.3

c) 0.4

d) 0.1

Question 2: How many colleges receive the accreditation of AAA?

Question 3: What is the highest overall score among the eight colleges ?

Question 4: How many colleges have overall scores between 31 and 40, both inclusive?

a) 0

b) 2

c) 1

d) 3

Instructions

In an election several candidates contested for a constituency. In any constituency, the winning candidate was the one who polled the highest number of votes, the first runner up was the one who polled the second highest number of votes, the second runner up was the one who polled the third highest number of votes, and so on. There were no ties (in terms of number of votes polled by the candidates) in any of the constituencies in this election. In an electoral system, a security deposit is the sum of money that a candidate is required to pay to the election commission before he or she is permitted to contest. Only the defeated candidates (i.e., one who is not the winning candidate) who fail to secure more than one sixth of the valid votes polled in the constituency, lose their security deposits.

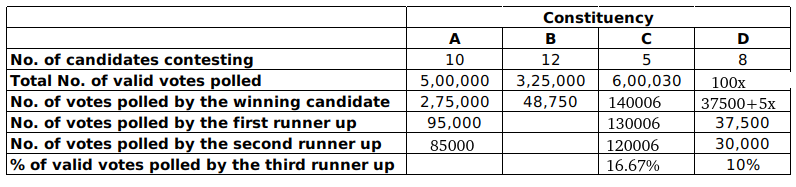
The following table provides some incomplete information about votes polled in four constituencies: A, B, C and D, in this election .

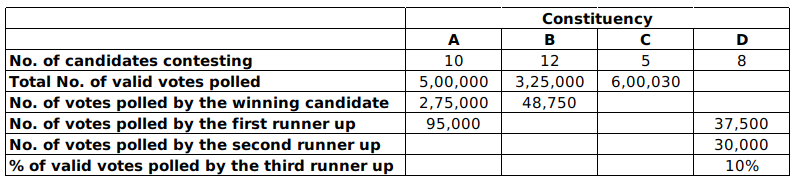
The following additional facts are known:

1. The first runner up polled 10,000 more votes than the second runner up in constituency A.
2. None of the candidates who contested in constituency C lost their security deposit. The difference in votes polled by any pair of candidates in this constituency was at least 10,000.
3. The winning candidate in constituency D polled 5% of valid votes more than that of the first runner up. All the candidates who lost their security deposits while contesting for this constituency, put together, polled 35% of the valid votes.

Question 5: What is the percentage of votes polled in total by all the candidates who lost their security deposits while contesting for constituency A?

Question 6: How many candidates who contested in constituency B lost their security deposit?

Question 7: What BEST can be concluded about the number of votes polled by the winning candidate in constituency C?

a) 1,40,010

b) between 1,40,005 and 1,40,010

c) less than 2,00,010

d) 1,40,006

Question 8: What was the number of valid votes polled in constituency D?

a) 1,25,000

b) 1,50,000

c) 1,75,000

d) 62,500

Question 9: The winning margin of a constituency is defined as the difference of votes polled by the winner and that of the first runner up. Which of the following CANNOT be the list of constituencies, in increasing order of winning margin?

a) D, B, C, A

b) B, D, C, A

c) B, C, D, A

d) D, C, B, A

Question 10: For all the four constituencies taken together, what was the approximate number of votes polled by all the candidates who lost their security deposit expressed as a percentage of the total valid votes from these four constituencies?

a) 38.25%

b) 23.54%

c) 23.91%

d) 32.00%

Join 7K MBA Aspirants Telegram Group

Download Highly Rated CAT preparation App

Answers & Solutions:

1) Answer (D)

It is given that:  High Q > Best Ed > Cosmopolitan  and Education Aid > A-one

We can say that High Q > Cosmopolitan

We can see that both High Q and Cosmopolitan got same points in reputation (R) and placement quality (P). High Q received more points in infrastructure (I) than Cosmopolitan whereas Cosmopolitan received more points in faculty Quality (F) than High Q.

Hence, we can say that Infrastructure’s weight should be greater than Faculty quality. i.e.   I > F

Similarly, We can see that both Best Ed and Cosmopolitan got same points in faculty Quality (F) and placement quality (P). Best Ed received more points in reputation (R) than Cosmopolitan whereas Cosmopolitan received more points in infrastructure (I) than Best Ed.

Hence, we can say that reputation’s weight should be greater than infrastructure. i.e.   R > I

Similarly, We can see that both Education Aid and A-one got same points in faculty Quality (F) and reputation (R). Education Aid received more points in infrastructure (I) than A-one whereas A-one received more points in placement quality (P) than Education Aid.

Hence, we can say that reputation’s weight should be greater than infrastructure. i.e.   I > P

So basically there are two possible cases: R > I > P > F or  R > I > F > P

Case 1:   Order of weights assigned = R > I > P > F

R = 0.4, I = 0.3. P = 0.2, F = 0.1

In this case overall score received by Best Ed = 0.1*40+0.4*30+0.2*20+0.3*20 = 26

In this case overall score received by High Q = 0.1*30+0.4*20+0.2*20+0.3*40 = 27

We can see that High Q’s overall score is higher than Best Ed. Hence, this is a possible case.

Case 2:   Order of weights assigned = R > I > F > P

R = 0.4, I = 0.3. P = 0.1, F = 0.2

In this case overall score received by Best Ed = 0.2*40+0.4*30+0.1*20+0.3*20 = 28

In this case overall score received by High Q = 0.2*30+0.4*20+0.1*20+0.3*40 = 28

We can see that High Q’s overall score is not greater than the overall score received Best Ed. Hence, this case is not possible.

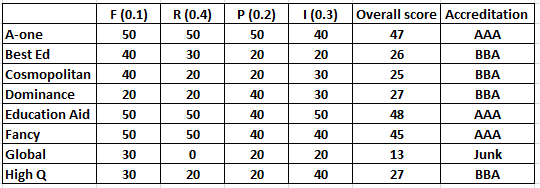
Now that we know the weight of each parameter, we can calculate the overall score and accreditation received by each college.

We can see that weight of the faculty quality parameter = 0.1. Hence,option D is the correct answer.

2) Answer: 3

It is given that:  High Q > Best Ed > Cosmopolitan  and Education Aid > A-one

We can say that High Q > Cosmopolitan

We can see that both High Q and Cosmopolitan got same points in reputation (R) and placement quality (P). High Q received more points in infrastructure (I) than Cosmopolitan whereas Cosmopolitan received more points in faculty Quality (F) than High Q.

Hence, we can say that Infrastructure’s weight should be greater than Faculty quality. i.e.   I > F

Similarly, We can see that both Best Ed and Cosmopolitan got same points in faculty Quality (F) and placement quality (P). Best Ed received more points in reputation (R) than Cosmopolitan whereas Cosmopolitan received more points in infrastructure (I) than Best Ed.

Hence, we can say that reputation’s weight should be greater than infrastructure. i.e.   R > I

Similarly, We can see that both Education Aid and A-one got same points in faculty Quality (F) and reputation (R). Education Aid received more points in infrastructure (I) than A-one whereas A-one received more points in placement quality (P) than Education Aid.

Hence, we can say that reputation’s weight should be greater than infrastructure. i.e.   I > P

So basically there are two possible cases: R > I > P > F or  R > I > F > P

Case 1:   Order of weights assigned = R > I > P > F

R = 0.4, I = 0.3. P = 0.2, F = 0.1

In this case overall score received by Best Ed = 0.1*40+0.4*30+0.2*20+0.3*20 = 26

In this case overall score received by High Q = 0.1*30+0.4*20+0.2*20+0.3*40 = 27

We can see that High Q’s overall score is higher than Best Ed. Hence, this is a possible case.

Case 2:   Order of weights assigned = R > I > F > P

R = 0.4, I = 0.3. P = 0.1, F = 0.2

In this case overall score received by Best Ed = 0.2*40+0.4*30+0.1*20+0.3*20 = 28

In this case overall score received by High Q = 0.2*30+0.4*20+0.1*20+0.3*40 = 28

We can see that High Q’s overall score is not greater than the overall score received Best Ed. Hence, this case is not possible.

Now that we know the weight of each parameter, we can calculate the overall score and accreditation received by each college.

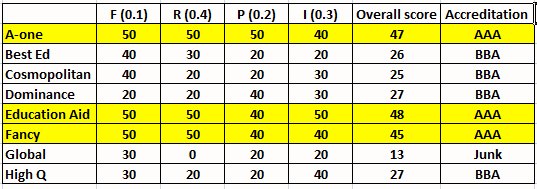
From the table, we can see that three received the accreditation of AAA.

3) Answer: 48

It is given that:  High Q > Best Ed > Cosmopolitan  and Education Aid > A-one

We can say that High Q > Cosmopolitan

We can see that both High Q and Cosmopolitan got same points in reputation (R) and placement quality (P). High Q received more points in infrastructure (I) than Cosmopolitan whereas Cosmopolitan received more points in faculty Quality (F) than High Q.

Hence, we can say that Infrastructure’s weight should be greater than Faculty quality. i.e.   I > F

Similarly, We can see that both Best Ed and Cosmopolitan got same points in faculty Quality (F) and placement quality (P). Best Ed received more points in reputation (R) than Cosmopolitan whereas Cosmopolitan received more points in infrastructure (I) than Best Ed.

Hence, we can say that reputation’s weight should be greater than infrastructure. i.e.   R > I

Similarly, We can see that both Education Aid and A-one got same points in faculty Quality (F) and reputation (R). Education Aid received more points in infrastructure (I) than A-one whereas A-one received more points in placement quality (P) than Education Aid.

Hence, we can say that reputation’s weight should be greater than infrastructure. i.e.   I > P

So basically there are two possible cases: R > I > P > F or  R > I > F > P

Case 1:   Order of weights assigned = R > I > P > F

R = 0.4, I = 0.3. P = 0.2, F = 0.1

In this case overall score received by Best Ed = 0.1*40+0.4*30+0.2*20+0.3*20 = 26

In this case overall score received by High Q = 0.1*30+0.4*20+0.2*20+0.3*40 = 27

We can see that High Q’s overall score is higher than Best Ed. Hence, this is a possible case.

Case 2:   Order of weights assigned = R > I > F > P

R = 0.4, I = 0.3. P = 0.1, F = 0.2

In this case overall score received by Best Ed = 0.2*40+0.4*30+0.1*20+0.3*20 = 28

In this case overall score received by High Q = 0.2*30+0.4*20+0.1*20+0.3*40 = 28

We can see that High Q’s overall score is not greater than the overall score received Best Ed. Hence, this case is not possible.

Now that we know the weight of each parameter, we can calculate the overall score and accreditation received by each college.

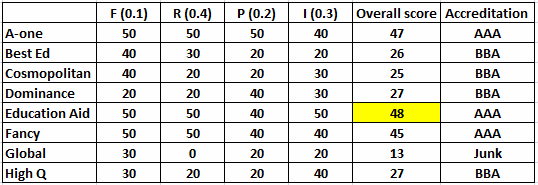
From the table we can see that Education Aid scored the highest overall score = 48.

4) Answer (A)

It is given that:  High Q > Best Ed > Cosmopolitan  and Education Aid > A-one

We can say that High Q > Cosmopolitan

We can see that both High Q and Cosmopolitan got same points in reputation (R) and placement quality (P). High Q received more points in infrastructure (I) than Cosmopolitan whereas Cosmopolitan received more points in faculty Quality (F) than High Q.

Hence, we can say that Infrastructure’s weight should be greater than Faculty quality. i.e.   I > F

Similarly, We can see that both Best Ed and Cosmopolitan got same points in faculty Quality (F) and placement quality (P). Best Ed received more points in reputation (R) than Cosmopolitan whereas Cosmopolitan received more points in infrastructure (I) than Best Ed.

Hence, we can say that reputation’s weight should be greater than infrastructure. i.e.   R > I

Similarly, We can see that both Education Aid and A-one got same points in faculty Quality (F) and reputation (R). Education Aid received more points in infrastructure (I) than A-one whereas A-one received more points in placement quality (P) than Education Aid.

Hence, we can say that reputation’s weight should be greater than infrastructure. i.e.   I > P

So basically there are two possible cases: R > I > P > F or  R > I > F > P

Case 1:   Order of weights assigned = R > I > P > F

R = 0.4, I = 0.3. P = 0.2, F = 0.1

In this case overall score received by Best Ed = 0.1*40+0.4*30+0.2*20+0.3*20 = 26

In this case overall score received by High Q = 0.1*30+0.4*20+0.2*20+0.3*40 = 27

We can see that High Q’s overall score is higher than Best Ed. Hence, this is a possible case.

Case 2:   Order of weights assigned = R > I > F > P

R = 0.4, I = 0.3. P = 0.1, F = 0.2

In this case overall score received by Best Ed = 0.2*40+0.4*30+0.1*20+0.3*20 = 28

In this case overall score received by High Q = 0.2*30+0.4*20+0.1*20+0.3*40 = 28

We can see that High Q’s overall score is not greater than the overall score received Best Ed. Hence, this case is not possible.

Now that we know the weight of each parameter, we can calculate the overall score and accreditation received by each college.

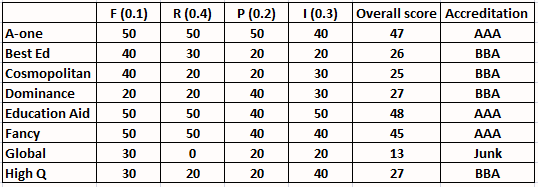
From the table we can see that none of the mentioned college received an overall scores between 31 and 40, both inclusive. Hence, option A is the correct answer.

5) Answer: 9

It’s given in the question that the first runner up polled 10,000 more votes than the second runner up in constituency A. Now the first runner up has got 95000 votes, hence the second runner up will get 85000 votes.

Now the remaining votes will be 500000-275000-95000-85000=45000

From 2, None of the candidates who contested in constituency C lost their security deposit. The difference in votes polled by any pair of candidates in this constituency was at least 10,000 => the person who got 5th highest votes must have got > 600030/6 => $\ge$ 100006. Since it is also given that the difference of votes is $\ge$ 10000, the only possible case is winner, 1st runner up, 2nd runner up, 3rd runner up, 4th runner up must have got 140006,130006,120006,110006,100006 respectively which sums upto exactly 600030.

Let the number of votes polled in D be 100x.

From 3, The winning candidate in constituency D must have got 15x+37500

The table now looks like:

Total votes in A = 500000 => the candidates who got $\le$ 83333 must have lost their security deposits => candidates till 2nd runner up didn’t lose their deposit =>all the candidates who received 500000-275000-95000-85000=45000 lost their deposits.

The percentage of votes polled in total by all the candidates who lost their security deposits while contesting for constituency A = 45000*100/500000 =9%

6) Answer: 11

It’s given in the question that the first runner up polled 10,000
more votes than the second runner up in constituency A. Now the first
runner up has got 95000 votes, hence the second runner up will get 85000
votes.

Now the remaining votes will be 500000-275000-95000-85000=45000

From
2, None of the candidates who contested in constituency C lost their
security deposit. The difference in votes polled by any pair of
candidates in this constituency was at least 10,000 => the person who
got 5th highest votes must have got > 600030/6 => $\ge$ 100006.
Since it is also given that the difference of votes is $\ge$ 10000,
the only possible case is winner, 1st runner up, 2nd runner up, 3rd
runner up, 4th runner up must have got
140006,130006,120006,110006,100006 respectively which sums upto exactly
600030.

Let the number of votes polled in D be 100x.

From 3, The winning candidate in constituency D must have got 5x+37500

The table now looks like:

In constituency B, the mark for not losing the security deposit is 1/6(325000) or 54,167.

But winner himself/herself got < 54167 => all the other candidates lost their security deposits.

11 is the correct answer,

7) Answer (D)

It’s given in the question that the first runner up polled 10,000
more votes than the second runner up in constituency A. Now the first
runner up has got 95000 votes, hence the second runner up will get 85000
votes.

Now the remaining votes will be 500000-275000-95000-85000=45000

From
2, None of the candidates who contested in constituency C lost their
security deposit. The difference in votes polled by any pair of
candidates in this constituency was at least 10,000 => the person who
got 5th highest votes must have got > 600030/6 => $\ge$ 100006.
Since it is also given that the difference of votes is $\ge$ 10000,
the only possible case is winner, 1st runner up, 2nd runner up, 3rd
runner up, 4th runner up must have got
140006,130006,120006,110006,100006 respectively which sums upto exactly
600030.

Let the number of votes polled in D be 100x.

From 3, The winning candidate in constituency D must have got  37500+5x.

The table now looks like:

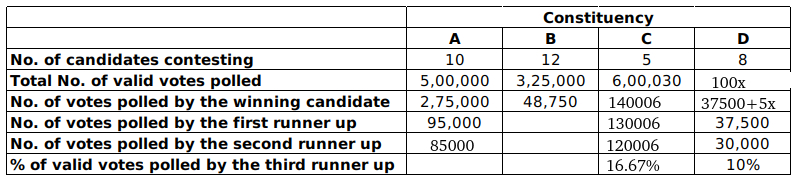
Number of votes polled to winning candidate must be 140006.

8) Answer (C)

It’s given in the question that the first runner up polled 10,000
more votes than the second runner up in constituency A. Now the first
runner up has got 95000 votes, hence the second runner up will get 85000
votes.

Now the remaining votes will be 500000-275000-95000-85000=45000

From
2, None of the candidates who contested in constituency C lost their
security deposit. The difference in votes polled by any pair of
candidates in this constituency was at least 10,000 => the person who
got 5th highest votes must have got > 600030/6 => $\ge$ 100006.
Since it is also given that the difference of votes is $\ge$ 10000,
the only possible case is winner, 1st runner up, 2nd runner up, 3rd
runner up, 4th runner up must have got
140006,130006,120006,110006,100006 respectively which sums upto exactly
600030.

From 3, Let the total votes in D be 100x => The winning candidate in constituency D must have got 37500+5x.

The table now looks like:

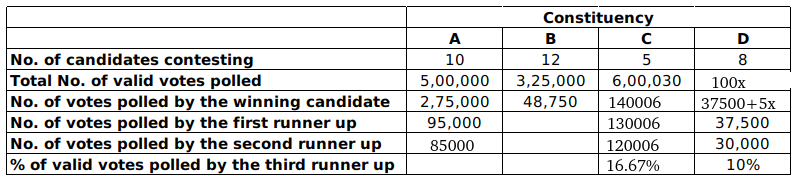
The candidates who didn’t lose the deposit must have got <16.67% => 3rd runner up must surely didn’t get the deposit.
Also,  the candidates who got security deposit must have got 65% of votes.
Case I:
Let top three candidates got the security deposit => 37500+5x+37500+30000 =65x => x=1750 => 100x= 175000

Case II:
Let top three candidates got the security deposit => 37500+5x+37500 =65x => 60x = 1250 => x=125000 but 16.66% of 125000 =20834  => 2nd runner up must got security deposit. So, this case is not valid.

The increasing order C will always come after D which is not happening in the third option. Hence that is the correct answer.

9) Answer (C)

It’s given in the question that the first runner up polled 10,000
more votes than the second runner up in constituency A. Now the first
runner up has got 95000 votes, hence the second runner up will get 85000
votes.

Now the remaining votes will be 500000-275000-95000-85000=45000

From
2, None of the candidates who contested in constituency C lost their
security deposit. The difference in votes polled by any pair of
candidates in this constituency was at least 10,000 => the person who
got 5th highest votes must have got > 600030/6 => $\ge$ 100006.
Since it is also given that the difference of votes is $\ge$ 10000,
the only possible case is winner, 1st runner up, 2nd runner up, 3rd
runner up, 4th runner up must have got
140006,130006,120006,110006,100006 respectively which sums upto exactly
600030.

From 3, The winning candidate in constituency D must have got 1.05*37500 = 39375.

Let the number of votes polled in D be 100x.

The table now looks like:

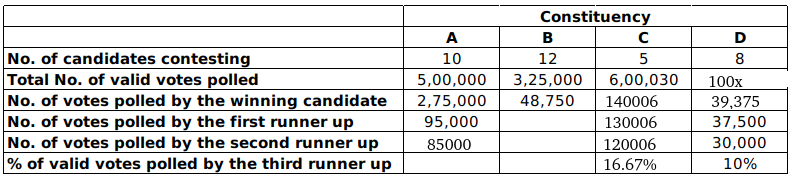
As calculated in the previous question, candidate D got 175000 votes. The winner got 5% more votes than first runner up, hence the winner got 0.05*175000 i.e 8750 more votes than first runner up . Thus 8750 is the winning margin for constituency D. Moreover margin in constituency is atleast 10000 . Hence in the increasing order C will always come after D which is not happening in the third option. Hence that is the correct answer.

10) Answer (C)

It’s given in the question that the first runner up polled 10,000
more votes than the second runner up in constituency A. Now the first
runner up has got 95000 votes, hence the second runner up will get 85000
votes.

Now the remaining votes will be 500000-275000-95000-85000=45000

From
2, None of the candidates who contested in constituency C lost their
security deposit. The difference in votes polled by any pair of
candidates in this constituency was at least 10,000 => the person who
got 5th highest votes must have got > 600030/6 => $\ge$ 100006.
Since it is also given that the difference of votes is $\ge$ 10000,
the only possible case is winner, 1st runner up, 2nd runner up, 3rd
runner up, 4th runner up must have got
140006,130006,120006,110006,100006 respectively which sums upto exactly
600030.

From 3, Let the total votes in D be 100x => The winning candidate in constituency D must have got 37500+5x.

The table now looks like:

The candidates who didn’t lose the deposit must have got <16.67% => 3rd runner up must surely didn’t get the deposit.
Also, the candidates who got security deposit must have got 65% of votes.
Case I:
Let top three candidates got the security deposit => 37500+5x+37500+30000 =65x => x=1750 => 100x= 175000

Case II:
Let top three candidates got the security deposit => 37500+5x+37500
=65x => 60x = 1250 => x=125000 but 16.66% of 125000 =20834 =>
2nd runner up must got security deposit. So, this case is not valid.

For all the constituencies lets look at the candidates who lost their security deposit.

A (500000-275000-95000-85000)=45000.

B (325000-48750)=276250

C (0) and D (61250)=175000-46250-30000-37500

Hence percentage will be 382500/1600000× 100=23.91%

Get 5 NMAT Mocks for Rs. 499

We hope this Tables DI Questions for NMAT pdf for NMAT exam will be highly useful for your Preparation.