SSC CHSL Previous Year Geometry Questions
SSC CHSL Geometry Previous Year Questions download PDF based on previous year question paper of SSC exams. 20 Very important Geometry Previous Year questions for SSC CHSL Exam.
Download SSC CHSL Previous Year Geometry Questions
Take a free mock test for SSC CHSL
Download SSC CHSL Previous Papers
Question 1: In ΔABC measure of angle B is 90°. If cosecA = 13/12, and AB = 10cm, then what is the length (in cm) of side AC?
a) 24
b) 12
c) 14
d) 26
Question 2: Two whole numbers are such that the cube of first number exceeds the cube of second by 61 and the ratio of the numbers is 5:4. What is the value of larger number?
a) 3
b) 4
c) 5
d) 6
Question 3: Chose the CORRECT option for the figure shoown below.
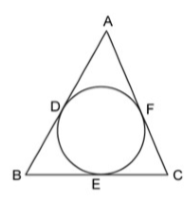
a) AD = AF
b) BD = BE
c) CE = FC
d) All options are correct.
Question 4: Calculate the length of the tangent (in cm) which is drawn from a point at a distance of 13 cm from the centre and the largest chord of that circle is 10 cm.
a) 10
b) 12
c) 15
d) 16
Question 5: The area and the length of one of the diagonals of a rhombus is 54 cm2 and 9 cm respectively. Find the length of its other diagonal (in cm).
a) 6
b) 24
c) 12
d) 18
SSC CHSL Study Material (FREE Tests)
Question 6: Calculate the area (in $cm^{2}$ ) of a circle of radius 10.5 cm.
a) 693
b) 157.5
c) 315
d) 346.5
Question 7: Find the total surface area (in $cm^{2}$ ) of a hemisphere of diameter 42 cm.
a) 4158
b) 5782
c) 6321
d) 7782
Question 8: In ΔXYZ measure of angle Y is 90° . If sinX = 4/5, and XY = 6cm, then what is the length (in cm) of side YZ?
a) 10
b) 5
c) 8
d) 4
Question 9: Find the square root of 1485961.
a) 1213
b) 1219
c) 1229
d) 1239
Question 10: The triangle in which the orthocenter, circumcentre, Incenter and the centroid coincide each other at a point is known as _____________.
a) isosceles triangle
b) equilateral triangle
c) right angled triangle
d) obtuse angled triangle
Question 11: If the radius of a circle is decreased to 25% of its original value, calculate the percentage decrease in the area of the circle.
a) 25%
b) 43.75%
c) 50%
d) 93.75%
Question 12: The perimeter and the breadth of a rectangle are 60 cm and 14 cm respectively. Find its area (in cm²).
a) 112
b) 448
c) 224
d) 336
Question 13: If the perimeter of a semi-circle is 108 cm, then find its radius (in cm).
a) 42
b) 28
c) 56
d) 21
Question 14: Find the volume (in $cm^{3}$) of a cube of side 7.5 cm.
a) 421.875
b) 77.145
c) 39.245
d) 24.435
Question 15: The height of the equilateral triangle is 9 cm. What is the radius (in cm) of the circle circumscribing the three vertices?
a) 3
b) 6
c) 9
d) 12
FREE SSC MATERIAL – 18000 FREE QUESTIONS
Question 16: What is that least number that must be added to the product 684 × 686 to make it a perfect square?
a) 685
b) 1
c) 684
d) 686
Question 17: The length of the diagonal and the breadth of a rectangle are 25 cm and 7 cm respectively. Find its perimeter (in cm).
a) 124
b) 41
c) 82
d) 62
Question 18: If a regular polygon has 6 sides then the measure of its interior angle is greater than the measure of its exterior angle by how many degrees?
a) $90^\circ$
b) $100^\circ$
c) $60^\circ$
d) $108^\circ$
Question 19: The curved surface area and the slant height of a right circular cone are 99 cm2 and 9 cm respectively. Find its diameter (in cm).
a) 3.5
b) 7
c) 14
d) 10.5
Question 20: Determine the largest 4 digit number which is a perfect square.
a) 9999
b) 9702
c) 9604
d) 9801
DOWNLOAD APP TO ACESSES DIRECTLY ON MOBILE
Answers & Solutions:
1) Answer (D)
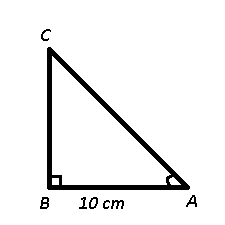
Given : AB = 10 cm and cosec A = 13/12
=> $cosecA=\frac{AC}{BC}=\frac{13}{12}$
Let $AC=13x$ and $BC=12x$
In right triangle ABC, => $(AC)^2=(AB)^2+(BC)^2$
=> $(13x)^2=(10)^2+(12x)^2$
=> $169x^2-144x^2=100$
=> $25x^2=100$
=> $x^2=\frac{100}{25}=4$
=> $x=\sqrt4=2$
$\therefore$ $AC=13\times2=26$ cm
=> Ans – (D)
2) Answer (C)
Let the numbers be $5x$ and $4x$
According to ques,
=> $(5x)^3-(4x)^3=61$
=> $125x^3-64x^3=61x^3=61$
=> $x^3=\frac{61}{61}=1$
=> $x=\sqrt[3]{1}=1$
$\therefore$ Larger number = $5\times1=5$
=> Ans – (C)
3) Answer (D)
If two tangents are drawn to a circle from one external point, then their tangent segments (lines joining the external point and the points of tangency) are equal.
=> AD = AF , BD = BE , CE = CF
Thus, all options are correct.
=> Ans – (D)
4) Answer (B)
Given : Largest chord in a circle is the diameter, => radius OA = $\frac{10}{2}=5$ cm and OB = $13$ cm
To find : AB = ?
Solution : In right $\triangle$ OAB,
=> $(AB)^2=(OB)^2-(OA)^2$
=> $(AB)^2=(13)^2-(5)^2$
=> $(AB)^2=169-25=144$
=> $AB=\sqrt{144}=12$ cm
=> Ans – (B)
5) Answer (C)
Let length of one diagonal = $d$ cm and length of other diagonal = 9 cm
=> Area of rhombus = $\frac{1}{2}\times d_1d_2$
=> $\frac{1}{2}\times9\times d=54$
=> $d=\frac{54\times2}{9}$
=> $d=12$ cm
=> Ans – (C)
6) Answer (D)
Radius of circle = $r=10.5$ cm
=> Area = $\pi r^2$
= $\frac{22}{7}\times10.5\times10.5$
= $22\times1.5\times10.5=346.5$ $cm^2$
=> Ans – (D)
7) Answer (A)
Radius of hemisphere, $r=\frac{42}{2}=21$ cm
Total surface area = $3\pi r^2$
= $3\times\frac{22}{7}\times (21)^2$
= $66\times3\times21=4158$ $cm^2$
=> Ans – (A)
8) Answer (C)
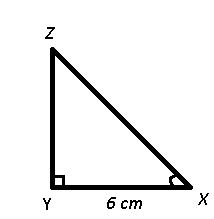
Given : XY = 6 cm and sinX = 4/5 ———(i)
To find : YZ = ?
Solution : $cosX=\sqrt{1-sin^2X}$
=> $cosX=\sqrt{1-\frac{16}{25}}=\sqrt{\frac{9}{25}}=\frac{3}{5}$ ———-(ii)
Dividing equation (i) by (ii), => $tanX=\frac{4}{3}$
In right $\triangle$ XYZ,
=> $tan(X)=\frac{YZ}{XY}$
=> $\frac{4}{3}=\frac{YZ}{6}$
=> $YZ=\frac{4}{3}\times6=8$ cm
=> Ans – (C)
9) Answer (B)
Factorization of $1485961 = 23^2\times53^2$
=> Square root = $\sqrt{1485961}=\sqrt{23^2\times53^2}$
= $23\times53=1219$
=> Ans – (B)
10) Answer (B)
Only in an equilateral triangle, the orthocenter, circumcentre, Incenter and the centroid coincide each other at a point.
=> Ans – (B)
11) Answer (B)
Let the radius of the circle initially = $r=20$ cm
=> Area = $A=\pi r^2=\pi(20)^2=400\pi$
New radius = $r’=20-(\frac{25}{100}\times20)=15$ cm
=> New Area = $A’=\pi(15)^2=225\pi$
$\therefore$ Percent decrease in area = $\frac{(400\pi-225\pi)}{400\pi}\times100$
= $\frac{175}{4}=43.75\%$
=> Ans – (B)
12) Answer (C)
Let $l$ be the length of rectangle and breadth, $b=14$ cm
=> Perimeter = $2(l+b)=60$
=> $l+14=\frac{60}{2}=30$
=> $l=30-14=16$ cm
$\therefore$ Area = $16\times14=224$ $cm^2$
=> Ans – (C)
13) Answer (D)
Let radius of semi circle = $r$ cm
=> Perimeter of semi circle = $\pi r+2r=108$
=> $r(\frac{22}{7}+2)=108$
=> $r(\frac{22+14}{7})=108$
=> $r=108\times\frac{7}{36}$
=> $r=3\times7=21$ cm
=> Ans – (D)
14) Answer (A)
Side of cube = $a=7.5$ cm
=> Volume of cube = $a^3$
= $(7.5)^3=421.875$ $cm^3$
=> Ans – (A)
15) Answer (B)
ABC is an equilateral triangle with height = median = 9 cm
Now, O is the circumcentre of the triangle and it divides the median in the ratio 2:1
=> $AO=\frac{2}{(2+1)}\times9$
=> $AO=\frac{2}{3}\times3$
=> $AO=2\times3=6$ cm
=> Ans – (B)
16) Answer (B)
Number = $684\times686$
= $684\times(684+2)$
= $(684)^2+2(684)$
Now, to make it a perfect square, = $(684)^2+2(684)(1)+(1)^2$
= $(684+1)^2=(685)^2$
$\therefore$ 1 is added to make it a perfect square.
=> Ans – (B)
17) Answer (D)
Let length of rectangle = $l$ cm and breadth = $7$ cm
Also, diagonal = $d=25$ cm
=> $l^2=d^2-b^2$
=> $l=\sqrt{(25)^2-(7)^2}$
=> $l=\sqrt{625-49}=\sqrt{576}$
=> $l=24$ cm
$\therefore$ Perimeter = $2(l+b)$
= $2\times(24+7)=62$ cm
=> Ans – (D)
18) Answer (C)
Sum of all interior angles of regular polygon with $n$ sides = $(n-2)\times180^\circ$
=> Sum of interior angles of a regular hexagon = $(6-2)\times180^\circ=720^\circ$
Also, sum of exterior angle of an polygon = $360^\circ$
$\therefore$ Required difference = $\frac{(720-360)}{6}$
= $\frac{360^\circ}{6}=60^\circ$
=> Ans – (C)
19) Answer (B)
Let radius of cone = $r$ cm and slant height of cone = $l=9$ cm
Curved surface area of cone = $\pi rl$
=> $\frac{22}{7}\times r\times9=99$
=> $r=\frac{99}{9}\times\frac{7}{22}$
=> $r=\frac{7}{2}=3.5$ cm
$\therefore$ Diameter of cone = $2\times3.5=7$ cm
=> Ans – (B)
20) Answer (D)
9999 is the largest 4 digit number and $100^2= 10000$
This means that the closest square root of the largest perfect square is most likely 99. So $99^2 =9801$ is the largest perfect square of four digits.
=> Ans – (D)
