Geometry Triangles Questions for SSC CHSL and MTS

Here you can download SSC CHSL & MTS 2022 – important SSC CHSL & MTS Geometry Triangles Questions PDF by Cracku. Very Important SSC CHSL & MTS 2022 and These questions will help your SSC CHSL & MTS preparation. So kindly download the PDF for reference and do more practice.

Download Geometry Triangles Questions for SSC CHSL and MTS

Enroll to 15 SSC CHSL 2022 Mocks At Just Rs. 149

Question 1: ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If the area of triangle ABC is 136 cm$^2$,
then the area of triangle BDE is equal to:

a) $36 cm^2$

b) $38 cm^2$

c) $24 cm^2$

d) $34 cm^2$

1) Answer (D)

Solution:

Let the side of the equilateral triangle ABC = a

$\Rightarrow$  BC = a

D is the mid-point of BC

$\Rightarrow$  BD = $\frac{a}{2}$

Side of the equilateral triangle BDE = $\frac{a}{2}$

Given, Area of the equilateral triangle ABC = 136 cm$^2$

$\Rightarrow$  $\frac{\sqrt{3}}{4}a^2=136$

$\therefore\ $Area of the equilateral triangle BDE = $\frac{\sqrt{3}}{4}\left(\frac{a}{2}\right)^2$

$=\frac{\sqrt{3}}{4}\times\frac{a^2}{4}$

$=\frac{1}{4}\times\frac{\sqrt{3}a^2}{4}$

$=\frac{1}{4}\times136$

$=$ 34 cm$^2$

Hence, the correct answer is Option D

Question 2: Two equilateral triangles of side $10\sqrt{3}$ cm are joined to form a quadrilateral. What is the altitude of the quadrilateral?

a) 12 cm

b) 14 cm

c) 16 cm

d) i5 cm

2) Answer (D)

Solution:

Given that  $10\sqrt{3}$ cm

We know the area of equilateral triangle = $ \frac{\sqrt {3}} {4} a^2 $   …… Eq (1)

and on the $\triangle DCB   is   also   given = \frac{1}{2} \times a \times h $   …… Eq (2)

then Eq(1) = Eq (2)

$ \frac{\sqrt {3}} {4} a^2  =   \frac{1}{2} \times a \times h $

$\Rightarrow h =  \frac{\sqrt{3}} {2} a $

$\Rightarrow h = \frac{\sqrt{3}} {2} \times 10\sqrt{3}$

$\Rightarrow h = 15 cm Ans

Question 3: The perimeters of two similar triangles ABC and PQRare 78 cm and 46.8 cm, respectively. If PQ = 11.7, then the length of AB is:

a) 19.5 cm

b) 23.4 cm

c) 24 cm

d) 20 cm

3) Answer (A)

Solution:

Triangles ABC and PQR are similar.
So,
$\frac{perimeter of ABC}{perimeter of PQR} = \frac{side of ABC}{side of PQR}$
$\frac{78}{46.8} = \frac{AB}{11.7}$
$\frac{78}{46.8} \times 11.7 = AB$
AB = 19.5 cm

Question 4: The sides of an isosceles triangles are 10 cm, 10 cm and 12 cm. What is the area of the triangle?

a) 60 $cm^2$

b) 48 $cm^2$

c) 40 $cm^2$

d) 44 $cm^2$

4) Answer (B)

Solution:

To find the area of the isosceles triangle ABC draw a perpendicular line from A to the base of the triangle BC and name that point as D such that it will become a right angled triangle.

Now,BD = CD =6cm.The area of the right angled triangle is given as = $\frac{1}{2}\times{b}\times{h}$,where b and h are base and height.
Height we can calculate from pythagoras theorem
$AD^{2}$ = $(AB^{2} – BD^{2})$
$\Rightarrow$ $AD^{2}$ = $(10^{2} – 6^{2})$
$\Rightarrow$ AD = 8cm.
The area of right angled now will be = $\frac{1}{2}\times{6}\times{8}$ = 24$cm^{2}$
The area of triangle ABC will be two times the area of triangle ADB = 24+24=48$cm^{2}$.
Hence option B is correct.

Question 5: Give that the ratio of altitudes of two triangles is 4 : 5, ratio of their areas is 3: 2. The ratio of their corresponding bases is

a) 8:15

b) 5:8

c) 15:8

d) 8:5

5) Answer (C)

Solution:

Given that ratio of altitudes of two triangles is 4:5

=> $\frac{h_{1}}{h_{2}}$=$\frac{4}{5}$

Also, Given that, ratio of areas of two triangles is 3:2

=> $\frac{\frac{1}{2} \times b_{1} \times h_{1}}{\frac{1}{2} \times b_{2} \times h_{2}}$ = $\frac{3}{2}$

=> $\frac{b_{1} \times 4}{ b_{2} \times 5}$ = $\frac{3}{2}$

=> $\frac{b_{1}}{ b_{2}}$ = $\frac{15}{8}$

Therefore, ratios of the bases is 15:8

Take a free SSC CHSL Tier-1 mock test

Download SSC CGL Tier-1 Previous Papers PDF

Question 6: Equilateral triangles are drawn on the hypotenuse and one of the perpendicular sides of a right-angled isosceles triangles. Their areas are H and A respectively. $\frac{A}{H}$ is equal to:

a) $\frac{1}{4}$

b) $\frac{1}{\sqrt[2]{2}}$

c) $\frac{1}{\sqrt{2}}$

d) $\frac{1}{2}$

6) Answer (D)

Solution:

Let the length of the two equal sides of right-angled isosceles triangle be x cm then hypotenuse be $x\sqrt{2}  cm$

Area of equilateral triangle drawn on hypotenuse (H) = $\frac{\sqrt{3}}{4}\times a^{2}=\frac{\sqrt{3}}{4}\times (x\sqrt{2})^2$

Area of equilateral triangle drawn on side (A) = $\frac{\sqrt{3}}{4}\times a^{2}=\frac{\sqrt{3}}{4}\times x^2$

$\frac{A}{H}=\left(\frac{\sqrt{3}}{4}\times x^{2}\right)\times\frac{4}{\sqrt{3}}\times\frac{1}{(x\sqrt{2})^2} = \frac{1}{2}$

Question 7: There is a polygon of 11 sides. How many triangles can be drawn by only using the vertices of the polygon?

a) 180

b) 150

c) 165

d) 175

7) Answer (C)

Solution:

Given,

Number of sides of the polygon = 11

$=$>  Number of vertices of the polygon = 11

Number of vertices of the triangle = 3

Number of possibilities of selecting 3 from 11 = $11_{C_3}$ =$\frac{11\times10\times9}{1\times2\times3}$ = $165$

$\therefore\ $Number of triangles that can be drawn by only using the vertices of the polygon of 11 sides = 165

Hence, the correct answer is Option C

Question 8: The ratio of the areas of two triangles ABC and PQR is 4: 5 and the ratio of their heights is 5 : 3. The ratio of the bases of triangle ABC to that of triangle PQR is:

a) 25 : 12

b) 12 : 25

c) 11 : 15

d) 15 : 11

8) Answer (B)

Solution:

We know that
Area = $\frac{1}{2}\times\ b\times\ h$
Now we can say
The ratio of areas of two triangles with bases b1 and b2 and heights h1 and h2 will be $\frac{\left(b1\ h1\right)}{b2\ h2}$
so we get
$\frac{4}{5}=\frac{\left(5b1\ \right)}{3b2}$
so b1:b2 =12:25

Question 9: The ratio of the areas of two triangles ABC and PQR is 3 : 5 and the ratio of their heights is 5 : 3. The ratio of the bases of triangle ABC to that of triangle PQR is:

a) 25 : 9

b) 9 : 25

c) 2 : 1

d) 1 : 1

9) Answer (B)

Solution:

Let the Areas  of $\triangle ABC$ and $\triangle PQR$  are  $3x:5x$

Let the Heights  of $\triangle ABC$ and $\triangle PQR$  are  $5y:3y$  and Bases are $B_{1}$ and $B_{2}$ respectively.

Area of $\triangle ABC$ = $\frac{1}{2} \times 5y\times B_{1}$ and Area of $\triangle PQR$ = $\frac{1}{2} \times3y\times B_{2}$

$\therefore \frac{3x}{5x} = \frac{\frac{1}{2} \times 5y\times B_{1}}{\frac{1}{2} \times3y\times B_{2}}$

$\Rightarrow \frac{B_{1}}{B_{2}} = \frac{9}{25}$

$\therefore$   $B_{1}:B_{2} = 9:25$

Question 10: The ratio of the area of two triangles is 2 : 3 and ratio of their height is 3 : 2. The ratio of their bases is:

a) 3:2

b) 4:9

c) 9:4

d) 2:3

10) Answer (B)

Solution:

Let height of the two triangles be 3 and 2 units respectively.

Let bases of the two triangles be $b_1$ and $b_2$ units respectively.

=> Ratio of area of triangles = $\frac{\frac{1}{2}\times b_1\times h_1}{\frac{1}{2}\times b_2\times h_2}=\frac{2}{3}$

=> $\frac{3b_1}{2b_2}=\frac{2}{3}$

=> $\frac{b_1}{b_2}=\frac{4}{9}$

$\therefore$ Required ratio = 4 : 9

=> Ans – (B)

Question 11: The ratio of the areas of two triangles is 1 : 2 and the ratio of their bases is 3 : 4. What will be the ratio of their height?

a) 1 : 3

b) 4 : 3

c) 2 : 1

d) 2 : 3

11) Answer (D)

Solution:

Let the bases of the triangles be 3x and 4x units.
Heights of the triangles be a and b units respectively.
Then, Ratio of their areas = $\dfrac{1}{2}\times3x\times a : \dfrac{1}{2}\times4x\times b = 3a : 4b$
Given, $3a : 4b = 1 : 2$
=> $3a\times2 = 4b\times1 => 6a = 4b$
=> $\dfrac{a}{b} = \dfrac{4}{6} = \dfrac{2}{3}$
Therefore, Their heights will be in the ratio 2 : 3.

Question 12: $PQRS$ is a square whose side is $20 cm$. By joining opposite vertices of $PQRS$ are get four triangles. What is the sum of the perimeters of the four triangles?

a) $40\surd2$

b) $80\surd2 + 80$

c) $40\surd2 + 40$

d) $40\surd2 + 80$

12) Answer (B)

Solution:

Side of square is 20 cm.

So, diagonal of square is 20√2 cm.

So,to calculate perimeter of triangle,we get to count each diagonal 2 times and 4 sides only one time .

So, required perimeter=4×20+4×20√2

=(80+80√2) cm.

B is correct choice.

Question 13: In the given figure. $ABCDEF$ is a regular hexagon whose side is 6 cm. $APF, QAB, DCR$ and $DES$ are equilateral triangles. What is the area (in $cm^2$) of the shaded region?

a) $24\surd3$

b) $18\surd3$

c) $72\surd3$

d) $36\surd3$

13) Answer (C)

Solution:

We have :

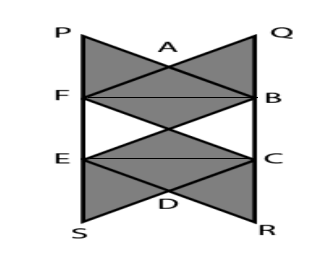
We here have 6 equilateral triangles of side 6cm so we can say a complete hexagon and half area of rectangle BCFE
Now In triangle ABF
using cosine rule
we get cos A = (6^2+6^2-BF^2)/2AF AB
we get BF $6\sqrt{\ 3}$
Area of shaded region = Area of hexagon + 0.5(Area of rectangle BFCE)
we get area = $6\times\ \frac{\sqrt{\ 3}}{4}\times\ 6\times\ 6\ +\ 6\sqrt{\ 3}\times\ 6\times\ 0.5$
= $54\sqrt{\ 3}+18\sqrt{\ 3}\ =72\sqrt{\ 3}$

Question 14: Which of the following options is/are CORRECT about the similarity of the two triangles?

a) The corresponding sides are proportional to each other.

b) The corresponding angles are equal.

c) The corresponding sides may or may not be equal to each other.

d) All option are correct.

14) Answer (D)

Solution:

If two triangles are similar, then the corresponding sides are proportional to each other. Also, the corresponding angles are equal, but the corresponding sides may or may not be equal to each other. Thus, all are correct.

=> Ans – (D)

Question 15: Consider the two equiangular triangles ABC and DEF having medians as AL and DM respectively as shown in figure below.

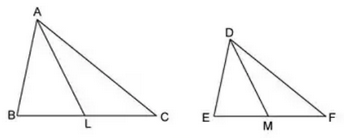Choose the correct option for the above situation.

a) $\frac{BC}{EF}=\frac{DM}{AL}$

b) $\frac{BC}{EF}=\frac{AL}{DM}$

c) $\frac{EF}{BC}=\frac{AL}{DM}$

d) All options are Correct

15) Answer (B)

Solution:

It is given that $\triangle$ ABC and $\triangle$ DEF are equiangular triangles, thus corresponding angles are equal.

=> $\triangle$ ABC $\sim\triangle$ DEF

=> Ratio of perimeter = $\frac{AB}{DE}=$ $\frac{BC}{EF}=$ $\frac{AC}{DF}$ ————-(i)

Since, AL and DM are medians, => Ratio of perimeter of $\triangle$ ABC to $\triangle$ DEF = $\frac{AL}{DM}$ ———–(ii)

From, equations (i) and (ii), we get :

=> $\frac{BC}{EF}=\frac{AL}{DM}$

=> Ans – (B)

Question 16: Consider the two similar triangles ABC and DEF. Which of the following is correct about the ratio of the area of the triangle ABC and DEF?

a) $(\frac{AB}{DE})=(\frac{EF}{BC})=(\frac{AC}{DF})$

b) $(\frac{AB}{DE})^2=(\frac{BC}{EF})^2=(\frac{AC}{DF})^2$

c) $(\frac{AB}{DE})=(\frac{BC}{EF})=(\frac{DF}{AC})$

d) None of these

16) Answer (B)

Solution:

It is given that $\triangle$ ABC $\sim\triangle$ DEF

=> $\frac{AB}{DE}=$ $\frac{BC}{EF}=$ $\frac{AC}{DF}$

Also, ratio of areas of two similar triangles is equal to the ratio of the square of the corresponding sides.

=> $\frac{ar(\triangle ABC)}{ar(\triangle DEF)}=$ $(\frac{AB}{DE})^2=(\frac{BC}{EF})^2=(\frac{AC}{DF})^2$

=> Ans – (B)

Question 17: Consider the following two triangles as shown in the figure below

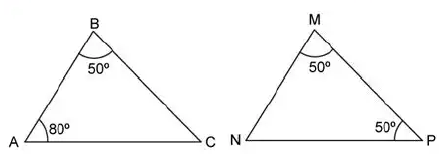
a) $\triangle BAC \sim\triangle NMP$

b) $\triangle BAC \sim\triangle MNP$

c) $\triangle CAB \sim\triangle NMP$

d) $\triangle BAC \sim\triangle PMN$

17) Answer (B)

Solution:

According to angle sum property : $\angle$ C = $50^\circ$ and $\angle$ N = $80^\circ$

Now, in $\triangle$ ABC and $\triangle$  MNP,

$\angle$ A = $\angle$ N = $80^\circ$

The remaining 2 angles are equal to $50^\circ$, thus either $\angle$ B = $\angle$ P or $\angle$ B = $\angle$ M

But $\angle$ A is corresponding to $\angle$ N.

Thus, $\triangle BAC \sim\triangle MNP$

=> Ans – (B)

Question 18: In a triangle ABC, a line is drawn from C which bisects AB at point D. Find the ratio of area of the triangles DBC and ABC.

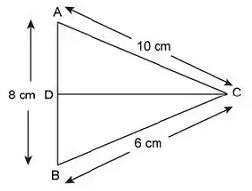
a) 1:1

b) 2:1

c) 1:2

d) 1:3

18) Answer (C)

Solution:

Given : CD bisects AB, => AD = DB = $\frac{8}{2}=4$ cm

To find : $\frac{ar(\triangle DBC)}{ar(\triangle ABC)}=?$

Solution : Clearly $\triangle$ ABC is a right angled triangle, $\because (10)^2=(8)^2+(6)^2$

Thus, AC is the hypotenuse and $\triangle$ ABC is right angled at B.

=> AB = 8 cm is the height of triangle

$\therefore$ $\frac{ar(\triangle DBC)}{ar(\triangle ABC)}=\frac{\frac{1}{2}\times(DB)\times(BC)}{\frac{1}{2}\times(AB)\times(BC)}$

= $\frac{4\times6}{8\times6}=\frac{1}{2}$

=> Ans – (C)

Question 19: If the $\angle A=\angle D$ and $\frac{AB}{DE}=\frac{AC}{DF}$ then both triangles ABC and DEF is similar by which of the following criteria?

a) SAS similarity

b) ASA similarity

c) AAA similarity

d) None of these

19) Answer (A)

Solution:

In $\triangle$ ABC and $\triangle$ DEF,

$\angle A=\angle D$     (given)

$\frac{AB}{DE}=\frac{AC}{DF}$    (given)

$\therefore$ $\triangle$ ABC $\sim$ $\triangle$ DEF by SAS similarity.

=> Ans – (A)

Question 20: If the ratio of the angle bisector segments of the two equiangular triangles are in the ratio of 3:2 then what is the ratio of the corresponding sides of the two triangles?

a) 2:3

b) 3:2

c) 6:4

d) 4:6

20) Answer (B)

Solution:

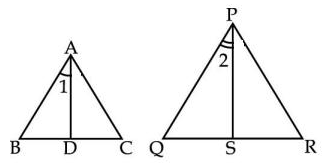
Given : $AD:PS=3:2$

To find : $AB : PQ=?$

Solution : The given triangles are equiangular, i.e. $\angle$ A = $\angle$ P , $\angle$ B = $\angle$ Q , $\angle$ C = $\angle$ R

Now, in $\triangle$ ABD and $\triangle$ PQS,

$\angle$ B = $\angle$ Q

$\angle$ BAD = $\angle$ QPS     [$\because$ $\angle$ A = $\angle$ P => $\frac{1}{2}$ $\angle$ A = $\frac{1}{2}$ $\angle$ P => $\angle$ BAD = $\angle$ QPS]

So, by A-A criterion of similarity, we have :

$\triangle$ ABD $\sim$ $\triangle$ PQS

=> $\frac{AB}{PQ}=\frac{AD}{PS}=\frac{3}{2}$

=> Ans – (B)

Question 21: Which of the following is the CORRECT option for the triangles having sides in the ratio of 3:4:6?

a) Acute angled

b) Obtuse angled

c) Right angled

d) Either acute or right angled

21) Answer (B)

Solution:

Let the sides of $\triangle$ ABC be $a,b,c$, where the largest side = $’c’$

If $c^2=a^2+b^2$, then the angle at $C$ is right angle.

If $c^2<a^2+b^2$, then the angle at $C$ is acute angle.

If $c^2>a^2+b^2$, then the angle at $C$ is obtuse angle.

Now, according to ques, => $6^2=36$

and $3^2+4^2=9+16=25$

$\therefore c^2>a^2+b^2$, hence it is an obtuse angled triangle.

=> Ans – (B)

Question 22: If the triangle  ABC and DEF follows the given equation, then these two triangles are similar by which of the following criterion ?
$\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}$

a) SAS similarity

b) SSS similarity

c) AAA similarity

d) None of the these

22) Answer (B)

Solution:

Given : $\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}$

=> AB = DE , BC = EF , AC = DF

Thus, all corresponding sides of the two triangles are equal.

$\therefore$ The two triangles are similar by SSS similarity.

=> Ans – (B)

Question 23: ∆ABC and ∆DEF are two similar triangles and the perimeter of ∆ABC and ∆DEF are 30 cm and 18 cm respectively. If length of DE = 36 cm, then length of AB is

a) 60 cm

b) 40 cm

c) 45 cm

d) 50 cm

23) Answer (A)

Solution:

It is given that ΔABC $\sim$ ΔDEF

Also, perimeter of ∆ABC and ∆DEF are 30 cm and 18 cm

=> Ratio of Perimeter of ΔABC : Perimeter of ΔDEF = Ratio of corresponding sides = AB : DE

= $\frac{30}{18} = \frac{AB}{36}$

=> AB = $\frac{5}{3} \times 36=60$ cm

=> Ans – (A)

Question 24: The perimeter of two similar triangles ABC and PQR are 36 cms and 24 cms respectively. If PQ = 10 cm then the length of AB is

a) 18 cm

b) 12 cm

c) 15 cm

d) 30 cm

24) Answer (C)

Solution:

It is given that ΔABC $\sim$ ΔPQR

Also, perimeter of ∆ABC and ∆PQR are 36 cm and 24 cm

=> Ratio of Perimeter of ΔABC : Perimeter of ΔPQR = Ratio of corresponding sides = AB : PQ

= $\frac{36}{24} = \frac{AB}{10}$

=> AB = $\frac{3}{2} \times 10=15$ cm

=> Ans – (C)

Question 25: The areas of two similar triangles ΔABC and ΔPQR are 36 sq cms and 9 sq cms respectively. If PQ = 4 cm then what is the length of AB (in cm)?

a) 16

b) 12

c) 8

d) 6

25) Answer (C)

Solution:

For similar triangles

Ratio of sides = $\sqrt{ \text(ratio of areas)}=\sqrt{36:9}=2:1$

AB/PQ = 2/1

AB/4 = 2/1

AB = 8

So the answer is option C.

shortlink to=”https://cracku.in/pay/c8f0w” color=”red” css_class=””]Enroll to 15 SSC MTS 2022 Mocks At Just Rs. 149[/shortlink]

Download SSC Preparation App

Enroll to 15 SSC CHSL 2022 Mocks At Just Rs. 149