Squares and Rectangles Questions for CAT PDF
Download important CAT Squares and Rectangles Questions with Solutions PDF based on previously asked questions in CAT exam. Practice Squares and Rectangles Questions with Solutions for CAT exam.
Download Squares and Rectangles Questions for CAT PDF
Question 1: 
What is the area under the line GHI-JKL in the given quadrilateral OPQR, knowing that all the small spaces are squares of the same area?
I. Length ABCDEQ is greater than or equal to 60.
II. Area OPQR is less than or equal to 1512.
a) The question can be answered with the help of statement I alone.
b) The question can be answered with the help of statement II, alone.
c) Both, statement I and statement II are needed to answer the question
d) The question cannot be answered even with the help of both the statements.
Question 2: A square piece of cardboard of sides ten inches is taken and four equal squares pieces are removed at the corners, such that the side of this square piece is also an integer value. The sides are then turned up to form an open box. Then the maximum volume such a box can have is
a) 72 cubic inches.
b) 24.074 cubic inches.
c) $\frac{2000}{27}$ cubic inches
d) 64 cubic inches.
Question 3: The adjoining figure shows a set of concentric squares. If the diagonal of the innermost square is 2 units, and if the distance between the corresponding corners of any two successive squares is 1 unit, find the difference between the areas of the eighth and the seventh squares, counting from the innermost square.
a) 10√2 sq. units
b) 30 sq. units
c) 35√2 sq. units
d) None of these
Question 4: Let $S_{1}, S_{2},…$ be the squares such that for each n ≥ 1, the length of the diagonal of $S_{n}$ is equal to the length of the side of $S_{n}+1$. If the length of the side of $S_{3}$ is 4 cm, what is the length of the side of $S_{n}$ ?
a) $2^[{\frac{2n+1}{2}}]$
b) $2.(n-1)$
c) $2^{n-1}$
d) $2^[{\frac{n+1}{2}}]$
e) None of these
Question 5: There are two squares S 1 and S 2 with areas 8 and 9 units, respectively. S 1 is inscribed within S 2 , with one corner of S 1 on each side of S 2 . The corners of the smaller square divides the sides of
the bigger square into two segments, one of length ‘a’ and the other of length ‘b’, where, b > a. A possible value of ‘b/a’, is:
a) ≥ 5 and < 8
b) ≥ 8 and < 11
c) ≥ 11 and < 14
d) ≥ 14 and < 17
e) > 17
Download CAT Quant Questions PDF
Question 6: A city has a park shaped as a right angled triangle. The length of the longest side of this park is 80 m. The Mayor of the city wants to construct three paths from the corner point opposite to the longest side such that these three paths divide the longest side into four equal segments. Determine the sum of the squares of the lengths of the three paths.
a) 4000 m
b) 4800 m
c) 5600 m
d) 6400 m
e) 7200 m
Question 7: In the figure below, the rectangle at the corner measures 10 cm × 20 cm. The corner A of the rectangle is also a point on the circumference of the circle. What is the radius of the circle in cm?
a) 10 cm
b) 40 cm
c) 50 cm
d) None of the above.
Question 8: In the given diagram, ABCD is a rectangle with AE = EF = FB. What is the ratio of the areas of CEF and that of the rectangle?
a) $\frac{1}{6}$
b) $\frac{1}{8}$
c) $\frac{1}{9}$
d) None of these
Question 9: In the figure given below, ABCD is a rectangle. The area of the isosceles right triangle ABE = 7 $cm^2$ ; EC = 3(BE). The area of ABCD (in $cm^2$) is
a) 21 $cm^2$
b) 28 $cm^2$
c) 42 $cm^2$
d) 56 $cm^2$
Question 10: The figure shows the rectangle ABCD with a semicircle and a circle inscribed inside in it as shown. What is the ratio of the area of the circle to that of the semicircle?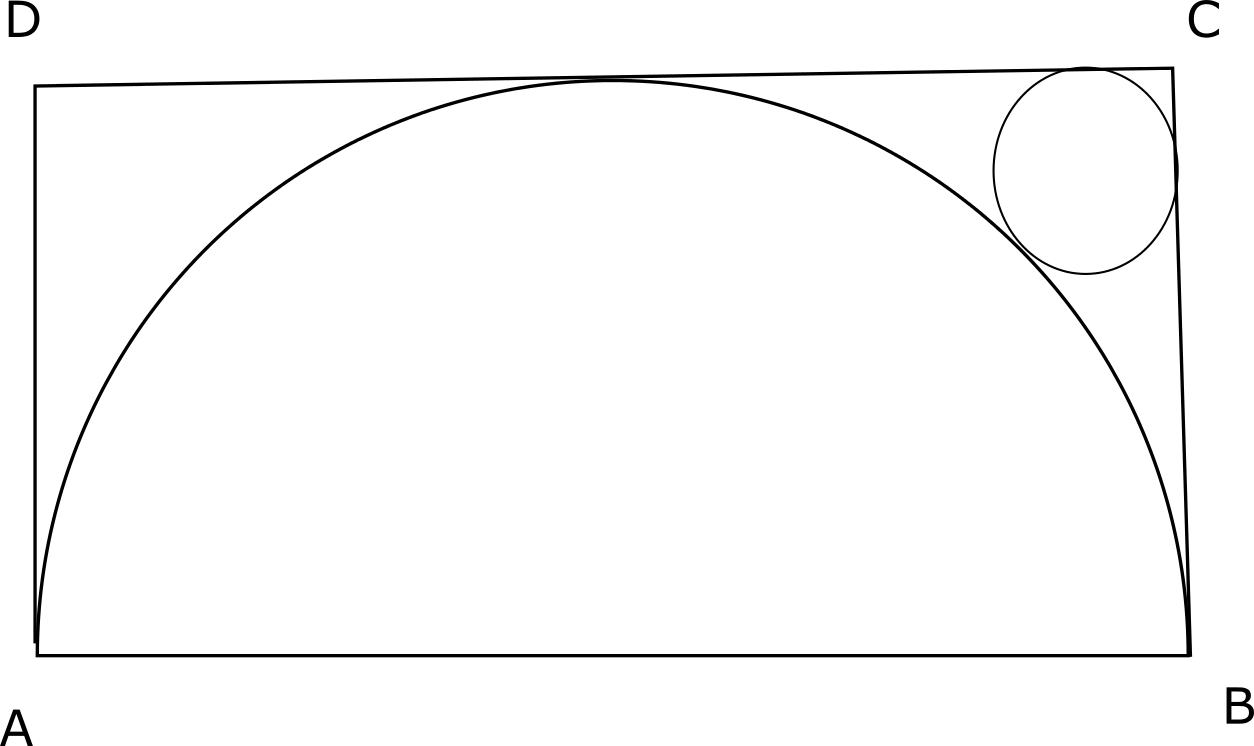
a) $(\sqrt2 -1)^{2}:1$
b) $2(\sqrt{2} -1)^2 :1$
c) $(\sqrt2-1)^2 :2$
d) None of these
Take a free CAT online mock test
Answers & Solutions:
1) Answer (C)
Let the side of the smallest square be x.
According to statement 1,$10x\geqslant 60$
$x\geqslant 6$
According to statement 2, $7x*6x\leq 1512$
$x\leq 6$
From both the statements x = 6 and the answer can be determined.
2) Answer (A)
Let the side of the square which is cut be x.
Volume of the cuboid so formed =$(10-2x)^2*x$
Put x = 1, 2, 3 and so on till 10
Maximum volume would be at x = 2
Volume of the cuboid so formed =$(10-2*2)^2*2 = 72$
3) Answer (B)
Diagonal of 8th square will be = 16
Side of 8th square = $\frac{16}{\sqrt2}$
Diagonal of 7th square will be = 14
Side of 7th square = $\frac{14}{\sqrt2}$
Difference in areas = $(\frac{16}{\sqrt2})^2 – (\frac{14}{\sqrt2})^2$ = 30
4) Answer (D)
Length of side of $S_{n + 1}$ = Length of diagonal of $S_n$
=> Length of side of $S_{n + 1}$ = $\sqrt{2}$ (Length of side of $S_{n}$)
=> $\frac{\textrm{Length of side of }S_{n + 1}}{\textrm{Length of side of }S_n} = \sqrt{2}$
=> Sides of $S_1 , S_2 , S_3 , S_4,…….., S_n$ form a G.P. with common ratio, $r = \sqrt{2}$
It is given that, $S_3 = ar^2 = 4$
=> $a (\sqrt{2})^2 = 4$
=> $a = \frac{4}{2} = 2$
$\therefore$ $n^{th}$ term of G.P. = $a (r^{n – 1})$
= $2 (\sqrt{2})^{n – 1}$
=$2^[{\frac{n+1}{2}}]$
5) Answer (D)
Area of $S_1 = 8$ sq. units
=> Side of $S_1 = PS = \sqrt{8} = 2 \sqrt{2}$ units
Similarly, Side of $S_2 = CD = \sqrt{9} = 3$ units
=> $a + b = 3$
In $\triangle$ PDS
=> $b^2 + a^2 = 8$
=> $b^2 + (3 – b)^2 = 8$
=> $b^2 + 9 + b^2 – 6b = 8$
=> $2b^2 – 6b + 1 = 0$
=> $b = \frac{6 \pm \sqrt{36 – 8}}{4} = \frac{6 \pm \sqrt{28}}{4}$
=> $b = \frac{3 + \sqrt{7}}{2}$ $(\because b > a)$
=> $a = 3 – \frac{3 + \sqrt{7}}{2} = \frac{3 – \sqrt{7}}{2}$
$\therefore \frac{b}{a} = \frac{\frac{3 + \sqrt{7}}{2}}{\frac{3 – \sqrt{7}}{2}}$
= $\frac{3 + \sqrt{7}}{3 – \sqrt{7}} \approx 15.9$
6) Answer (C)
To find : $(BD)^2 + (BE)^2 + (BF)^2 = ?$
AC = 80 m
AD = DE = EF = FC = 20
Let $AB = a$ and $BC = b$
In $\triangle$ ABC
$(a)^2 + (b)^2 = (80)^2$
Also, $(BE) = 1/2 (AC) = 40 $
=> $BE = 40$
Using Apollonius theorem in $\triangle$ ABE, as AD = DE
=> $(AB)^2 + (BE)^2 = 2 [(BD)^2 + (AD)^2]$
=> $(BD)^2 + 20^2 = \frac{1}{2} (a^2 + 40^2)$ ——–Eqn(I)
Similarly, for $\triangle$ BEC, as EF = FC
=> $(BE)^2 + (BC)^2 = 2 [(BF)^2 + (FC)^2]$
=> $(BF)^2 + 20^2 = \frac{1}{2} (b^2 + 40^2)$ ——–Eqn(II)
Adding eqns (I) & (II), we get :
=> $(BD)^2 + (BF)^2 + 20^2 + 20^2$ $= \frac{1}{2} (a^2 + 40^2 + b^2 + 40^2)$
=> $(BD)^2 + (BF)^2 + 20^2 + 20^2$ $= \frac{1}{2} (80^2 + 40^2 + 40^2)$
=> $(BD)^2 + (BF)^2 = 4800 – 800 = 4000$
$\therefore$ $(BD)^2 + (BE)^2 + (BF)^2 = 4000 + 40^2$
= $4000 + 1600 = 5600$
7) Answer (C)
As seen in the fig. we have a right angled triangle with sides r ,r-10 , r-20.
Using pythagoras we have $r^2 = (r-10)^2 + (r-20)^2$.
Solving the equation, we get r = 10 or 50.
But 10 is not possible , so r = 50.
Hence radius is 50.
8) Answer (A)
Area of triangle CEF = 1/2 * length of rectangle/3 * breadth of rectangle = Area of rectangle/6
So, required ratio = 1:6
9) Answer (D)
Let AB = BE = x
Area of triangle ABE = $x^2/2$ = 14; we get x = $\sqrt{14}$
So we have side BC = 4*$\sqrt{14}$
Now area is AB*BC = 14 *4 = 56 $cm^2$
10) Answer (D)
Let the center be O and the point at which the semicircle intersects CD be P.
Let the radius of the semicircle be R and the circle be r.
OP = R and OC = R$\sqrt{2}$
OC – OT = CC’ – TC’
$R\sqrt{2} – R – 2r$ = $r\sqrt{2} – r$
=> $R\sqrt{2} – R$ = $r\sqrt{2} + r$
=> r = $\frac{(\sqrt{2}-1)R}{\sqrt{2}+1}$
=> r = $(\sqrt{2}-1)^2$R
Ratio of areas will be $r^2 : \frac{R^2}{2}$ = $2(\sqrt{2}-1)^4$ : 1
Download CAT Previous Papers PDF
Download Free CAT Preparation App
We hope this CAT Squares and Rectangles Questions with Solutions PDF for CAT will be helpful to you.
