Sphere Questions for CAT PDF
Download important CAT Sphere Questions with Solutions PDF based on previously asked questions in CAT exam. Practice Sphere Questions with Solutions for CAT exam.
Download Sphere Questions for CAT PDF
Download CAT Quant Questions PDF
Question 1: It takes 2 liters to paint the surface of a solid sphere. If this solid sphere is sliced into 4 identical pieces, how many liters will be required to paint all the surfaces of these 4 pieces.
a) 2.2 liters
b) 2.5 liters
c) 3.0 liters
d) 4.0 liters
e) None of the above
Question 2: If a right circular cylinder of height 14 $cm$ is inscribed in a sphere of radius 8 $cm$, then the volume of the cylinder is:
a) 110 $cm^3$
b) 220 $cm^3$
c) 440 $cm^3$
d) 660 $cm^3$
Question 3: A cylinder, a Hemi-sphere and a cone stand on the same base and have the same heights. The ratio of the areas of their curved surface is:
a) $2:2:1$
b) $2:\sqrt{2}:1$
c) $\sqrt{2}:3:1$
d) None of the above
Question 4: Consider the volumes of the following objects and arrange them in decreasing order:
i. A parallelepiped of length 5 cm, breadth 3 cm and height 4 cm
ii. A cube of each side 4 cm.
iii. A cylinder of radius 3 cm and length 3 cm
iv. A sphere of radius 3 cm
a) iv,iii,ii,i
b) iv,ii,iii,i
c) iv,iii,i,ii
d) None of the above
Question 5: A spherical metal of radius 10 cm is molten and made into 1000 smaller spheres of equal sizes. In this process the surface area of the metal is increased by:
a) 1000 times
b) 100 times
c) 10 times
d) No change
e) None of the above
Take a free CAT online mock test
Answers & Solutions:
1) Answer (D)
2 litres are required to paint the surface of a solid sphere.
Surface area of the solid sphere = $4\pi*r^2$
Now, the solid sphere is cut into 4 identical parts. This is possible only when the sphere is cut into 4 quarter spheres.
After making the first cut, 2 hemispheres will be formed. 2 circles of area $\pi*r^2$ will get exposed in addition to the surface area of the sphere (the base surface of the bottom hemisphere and the base of the top hemisphere).
Now, another perpendicular cut will be made along the diameter of the sphere. 2 additional surfaces will get exposed again (one on left hemisphere and the another on the right hemisphere).
Area exposed after making 4 identical pieces = $4*\pi*r^2$ + $2*\pi*r^2$ + $2*\pi*r^2$
= $8*\pi*r^2$
2 litres of paint is required to paint an area of $4\pi*r^2$
=> 4 litres of paint will be required to paint an area of $8*\pi*r^2$.
Therefore, option D is the right answer.
2) Answer (D)
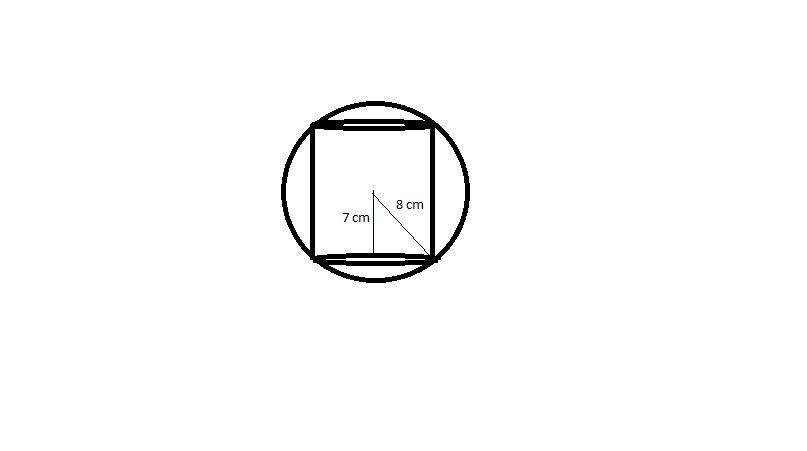
The radius of sphere is 8 $cm$. Then applying Pythagoras, the radius of base of cylinder is $\sqrt{15}$ $cm$
The height of cylinder is given as 14 $cm$. Volume of cylinder is $\pi$ $r^{2}$h
$\frac{22}{7}$* 15*14 = 660 $cm^3$
3) Answer (D)
The cylinder, hemisphere and cone stand on the same base and have the same height. Let the radius of the three solids be $r$ and the height be $h$.
Height of the hemisphere, $h$ = $r$ (Radius)
Curved surface area of the cylinder = $2*\pi*r*r$ = $2*\pi*r^2$
Curved surface area of the hemisphere = $2*\pi*r^2$
Curved surface area of the cone = $\pi*r*\sqrt{r^2+r^2}$ = $\pi*r*\sqrt{r^2+r^2}$ = $\pi*r^2*\sqrt{2}$
Ratio = $2:2:\sqrt{2}$ = $\sqrt{2}:\sqrt{2}:1$
As the answer is not among the given options, option D is the right answer.
4) Answer (A)
i. Volume of the parallelepiped of length 5 cm, breadth 3 cm and height 4 cm = 3*4*5 = 60 cm$^3$
ii. Volume of the cube of each side 4 cm = 4^3 = 64 cm$^3$
iii.Volume of the cylinder of radius 3 cm and length 3 cm = $\pi*3^2*3$ = 84.82 cm$^3$
iv. Volume of the sphere of radius 3 cm = $4/3*\pi*3^3$ = 113.09 cm$^3$
Therefore, we can say that volumes of the objects in decreasing order = iv,iii,ii,i.
Hence, option A is the correct answer.
5) Answer (E)
Radius of larger sphere = $R = 10$ cm
Let radius of each of the smaller spheres = $r$ cm
=> $\frac{4}{3} \pi R^3 = 1000 \times \frac{4}{3} \pi r^3$
=> $10^3 = 1000 r^3$
=> $r = \sqrt[3]{1} = 1$ cm
Initial surface area of sphere = $4 \pi R^2 = 4 \pi \times 100 = 400 \pi$
Final surface area of 1000 spheres = $1000 \times 4 \pi r^2 = 1000 \times 4 \pi = 4000 \pi$
$\therefore$ Increase in surface area = $4000 \pi – 400 \pi = 3600 \pi$
=> $\frac{3600 \pi}{400 \pi} = 9$ times
Download CAT Previous Papers PDF
Download Free CAT Preparation App
We hope this CAT Sphere Questions with Solutions PDF for CAT will be helpful to you.
