SBI PO Previous Year Puzzle Questions

Download SBI PO Puzzle Previous Year Questions & Answers PDF for SBI Clerk Prelims and Mains exam. Very Important SBI PO Puzzle questions on with solutions.

Download SBI PO Previous Year Puzzle Questions

790+ Mocks – Just Rs. 194 – Coupon SBIDREAM70

Take a Free SBI PO Mock Test

Download SBI PO Previous Papers PDF

Instructions

8 persons A, B, C, D, E, F, G, and H were born on the same date but on different years among 1990, 1992, 1993, 1995, 1998, 2002, 2003, and 2005, not necessarily in the same order. Further, the following information is known:

The difference between the ages of B and F is 10 years.
The difference between the ages of A and E is 7 years.
The difference between the ages of E and B is 1 year.
The difference between the ages of D and F is 1 year.
The difference between the ages of C and G is 8 years.
The difference between the ages of G and H is 7 years.

Question 1: Who is the oldest person in the group?

a) C

b) B

c) A

d) G

e) F

Question 2: Who among the following is older than F?

a) A

b) B

c) H

d) D

e) E

Question 3: If the sum of the ages of B and H is 10, what is the age of G?

a) 12 years

b) 13 years

c) 11 years

d) 15 years

e) 10 years

Instructions

6 friends A, B, C, D, E and F have a different number of coins with them. The total number of coins with them is 39. Also, it is known that the numbers of coins with the friends are 6 consecutive integers. Further, the following information is known.

1. The number of coins with C is a perfect square.
2. The number of coins with A is a prime number.
3. The number of coins with B is the average of the number of coins with E and F.
4. The difference between the number of coins with D and E is 4.
5. The difference between the number of coins with C and A is 2.

Question 4: What is the number of coins with F?

a) 4

b) 5

c) 6

d) 7

e) Can’t be determined

Question 5: What is the difference between the number of coins with C and B?

a) 4

b) 5

c) 6

d) 7

e) Can’t be determined

Take a Free Mock test for SBI PO

Download SBI PO Previous Papers PDF

Question 6: Which of the following is true?

a) The number of coins with F is a prime number.

b) The number of coins with F is divisible by 6.

c) The number of coins with F is divisible by 4.

d) The sum of the number of coins with B and D is divisible by 4.

e) None of the above.

Instructions

7 friends A, B, C, D, E, F and G have a different number of coins with them from 3-9. The number of coins with B is a prime number, but it is not 3. The number of coins with C is the average of the number of coins with A and E. F has an odd number of coins. 3 people have more number of coins than B, but less than E. Sum of the number of coins with B and A is equal to the number of coins with G.

Question 7: Who has 9 coins?

a) E

b) F

c) B

d) A

e) D

Question 8: 4 of the following are alike in a certain way. Find the odd man out.

a) A

b) B

c) D

d) F

e) E

Question 9: What is the difference between the number of coins with F and D?

a) 4

b) 1

c) 2

d) 0

e) 3

Question 10: P, Q, R, S, T, U and V are comparing their heights. S is the shortest. 3 people are taller than U but shorter than T and R is not one of them. P is taller than V but shorter than Q. R is taller than at least 2 people. How many people are shorter than R?

a) 6

b) 4

c) 3

d) 5

e) Cannot be determined

Banking 1 Year Plan – 350 Mocks for just Rs. 499

SBI PO Important Questions PDF 

Instructions

Read the paragraph and answer the questions that follow:
Aman, Bajrang, Chetan, Devesh, Emam, Hitesh and Kapish are seven footballers. Each of them is from a different nation from the following list (not necessarily in the same order) – India, Japan, China, Malaysia, Korea, Nepal and Fiji. Each of them owns mobile of a different brand namely Apple, Xiaomi, Samsung, Oppo, Vivo, Nokia and Blackberry. Bajrang is from Nepal and owns a Vivo mobile. The footballer from Fiji owns a Xiaomi phone. Emam owns an Oppo mobile. Chetan is from Malaysia and he doesn’t own an Apple mobile. Kapish owns a Blackberry phone and doesn’t belong to either Japan or China. The footballer from Korea owns a Nokia mobile. Emam is not from China. Aman doesn’t own a Xioami or a Nokia phone. Devesh is not from Fiji.

 

Question 11: Who is from India?

a) Hitesh

b) Devesh

c) Kapish

d) Bajrang

e) Aman

Question 12: From which of the following nations does Aman belong to?

a) Korea

b) Fiji

c) Japan

d) China

e) Nepal

Question 13: Which of the following brand’s phone is owned by Chetan?

a) Xioami

b) Samsung

c) Apple

d) Vivo

e) None of the above

Question 14: Which of the following combinations is correct?

a) Chetan – Malaysia

b) Emam – Japan

c) Hitesh – Fiji

d) Kapish – India

e) All are correct.

Question 15: Which of the following combinations is incorrect?

a) Devesh – Nokia

b) Hitesh – Xiaomi

c) Kapish – Blackberry

d) Aman – Samsung

e) More than one of the above

Banking Online Daily Tests

15000 Solved Questions – Free Banking Study Material

Instructions

Read the paragraph and answer the questions that follow:
Five players Virat, Rohit, Dhoni, Yuvi and Rahane live in five different rooms numbered from 1 to 5 not necessarily in the same order. Each player likes a different perfume among Azzaro, Sebastian, Armani, Davidoff and Guerlain, but not necessarily in the same order. Each player likes a different bowler among Steyn, Rabada, Lee, Boult and Amir.
We are given some additional information about the players:

1) Virat likes Amir and lives in the least numbered room.
2) The player who lives in the highest numbered room does not like Armani or Sebastian.
3) Yuvi likes Lee as well as Armani.
4) The one who likes Sebastian lives in a higher numbered room than the person who likes Azzaro.
5) The one who likes Rabada also likes Davidoff and lives in an even-numbered room.
6) Rahane lives in an odd-numbered room and likes Guerlain.
7) Dhoni likes Boult and lives in a room whose number is one greater the player who likes Davidoff.

Question 16: The one who likes Lee lives in room no.?

a) 1

b) 2

c) 3

d) 4

e) 5

Question 17: Who among the following players like Davidoff perfume?

a) Virat

b) Rohit

c) Dhoni

d) Yuvi

e) Rahane

Question 18: Which of the following statements is false?

a) Virat likes Azzaro.

b) Rohit likes Rabada.

c) Dhoni likes Guerlain.

d) Yuvi likes Armani

e) None of the above

Question 19: Who among the following likes Steyn?

a) Virat

b) Rohit

c) Dhoni

d) Yuvi

e) Rahane

Question 20: Which of the following combinations is correct?

a) Room no. 3 – Dhoni

b) Room no. 2 – Yuvi

c) Room no. 5 – Virat

d) Room no. 1 – Rahane

e) None of the above

Daily Free GK – Current Affairs Tests

Answers & Solutions:

1) Answer (A)

The difference between the ages of B and F is 10 years.
Therefore, B and F can be born in (1992,2002), (1993,2003), and (1995, 2005) in any order.
Difference between the ages of A and E is 7 years.
Therefore, A and E can be born in (1995,2002) and (1998,2005) in any order.
Difference between the ages of E and B is 1 year.
Among the pairs obtained so far, only (2002,2003) satisfy this condition. E could not have born in 2003. Therefore, E must have born in 2002 and B must have born in 2002. A must have born in 1995 and F must have born in 1993.

Difference between the ages of D and F is 1. Therefore, D must be born in 1992.

The difference between the ages of C and G is 8 years.
The difference between the ages of G and H is 7 years.
Only 3 years – 1990, 1998 and 2005 are remaining. Therefore, C must be born in 1990, G must be born in 1998 and H must be born in 2005.

The final arrangement is as follows:

1990 – C
1992 – D
1993 – F
1995 – A
1998 – G
2002 – E
2003 – B
2005 – H

C is the oldest person in the group. Therefore, option A is the right answer.

2) Answer (D)

The difference between the ages of B and F is 10 years.
Therefore, B and F can be born in (1992,2002), (1993,2003), and (1995, 2005) in any order.
Difference between the ages of A and E is 7 years.
Therefore, A and E can be born in (1995,2002) and (1998,2005) in any order.
Difference between the ages of E and B is 1 year.
Among the pairs obtained so far, only (2002,2003) satisfy this condition. E could not have born in 2003. Therefore, E must have born in 2002 and B must have born in 2002. A must have born in 1995 and F must have born in 1993.

Difference between the ages of D and F is 1. Therefore, D must be born in 1992.

The difference between the ages of C and G is 8 years.
The difference between the ages of G and H is 7 years.
Only 3 years – 1990, 1998 and 2005 are remaining. Therefore, C must be born in 1990, G must be born in 1998 and H must be born in 2005.

The final arrangement is as follows:

1990 – C
1992 – D
1993 – F
1995 – A
1998 – G
2002 – E
2003 – B
2005 – H

D is older than F. Therefore, option D is the right answer.

3) Answer (C)

The difference between the ages of B and F is 10 years.
Therefore, B and F can be born in (1992,2002), (1993,2003), and (1995, 2005) in any order.
Difference between the ages of A and E is 7 years.
Therefore, A and E can be born in (1995,2002) and (1998,2005) in any order.
Difference between the ages of E and B is 1 year.
Among the pairs obtained so far, only (2002,2003) satisfy this condition. E could not have born in 2003. Therefore, E must have born in 2002 and B must have born in 2002. A must have born in 1995 and F must have born in 1993.

Difference between the ages of D and F is 1. Therefore, D must be born in 1992.

The difference between the ages of C and G is 8 years.
The difference between the ages of G and H is 7 years.
Only 3 years – 1990, 1998 and 2005 are remaining. Therefore, C must be born in 1990, G must be born in 1998 and H must be born in 2005.

The final arrangement is as follows:

1990 – C
1992 – D
1993 – F
1995 – A
1998 – G
2002 – E
2003 – B
2005 – H

Let the age of H be x.
=> Age of B = x+2
It has been given that x+x+2 = 10
x = 4 years.

Age of H = 4 years.
=> Age of G = 4+7 = 11 years.
Therefore, option C is the right answer.

4) Answer (C)

Total number of coins are 39. Hence we can say that  A, B, C, D, E and F have 4,5,6,7,8 and 9 coins with them not necessarily in the same order.

In statement 1 it is given that the number of coins with C is a perfect square, hence C can have either 4 or 9 coins. By statement 5 we can say that A has either 6 ot 7 coins with him. But in statement 2 is is given that the number of coins with A is a prime number hence we can say that A has 7 coins and C has 9 coins.

The difference between the number of coins with D and E is 4 hence we can say that they have 4 and 8 coins in any order. Hence we can say that B and F have 5, 6 in any order.

Let us assume that B has 6 coins then F will have 5 coins. By statement 3 we can see that E must have 7 coins with him but A has 7 coins hence this case is not possible.

Let us assume that B has 5 coins then we can say that F has 6 coins. Also by statement 3 we can say that the number of coins with E is 4. Consequently D will have 8 coins.

4 – E

5 – B

6 – F

7 – A

8 – D

9 – C

From the arrangement we can see that F has 6 coins. Hence, option C is the correct answer.

5) Answer (A)

Total number of coins are 39. Hence we can say that  A, B, C, D, E and F have 4,5,6,7,8 and 9 coins with them not necessarily in the same order.

In statement 1 it is given that the number of coins with C is a perfect square, hence C can have either 4 or 9 coins. By statement 5 we can say that A has either 6 ot 7 coins with him. But in statement 2 is is given that the number of coins with A is a prime number hence we can say that A has 7 coins and C has 9 coins.
The difference between the number of coins with D and E is 4 hence we can say that they have 4 and 8 coins in any order. Hence we can say that B and F have 5, 6 in any order.

Let us assume that B has 6 coins then F will have 5 coins. By statement 3 we can see that E must have 7 coins with him but A has 7 coins hence this case is not possible.

Let us assume that B has 5 coins then we can say that F has 6 coins. Also by statement 3 we can say that the number of coins with E is 4. Consequently D will have 8 coins.

4 – E

5 – B

6 – F

7 – A

8 – D

9 – C

From the arrangement we can see that the difference between the number of coins with C and B = 9 – 5 = 4. Hence, option A is the correct answer.

6) Answer (B)

Total number of coins are 39. Hence we can say that  A, B, C, D, E and F have 4,5,6,7,8 and 9 coins with them not necessarily in the same order.

In statement 1 it is given that the number of coins with C is a perfect square, hence C can have either 4 or 9 coins. By statement 5 we can say that A has either 6 ot 7 coins with him. But in statement 2 is is given that the number of coins with A is a prime number hence we can say that A has 7 coins and C has 9 coins.  The difference between the number of coins with D and E is 4 hence we can say that they have 4 and 8 coins in any order. Hence we can say that B and F have 5, 6 in any order.

Let us assume that B has 6 coins then F will have 5 coins. By statement 3 we can see that E must have 7 coins with him but A has 7 coins hence this case is not possible.

Let us assume that B has 5 coins then we can say that F has 6 coins. Also by statement 3 we can say that the number of coins with E is 4. Consequently D will have 8 coins.

4 – E

5 – B

6 – F

7 – A

8 – D

9 – C

We can see that only option B is correct. Number of coins with F is 6 which is divisible by 6.

7) Answer (A)

The number of coins with B is a prime number, but it is not 3. Thus, the number of coins with B can be either 5 or 7.
3 people have more number of coins than B but less than E. This is possible only when B has 5 coins and E has 9 coins.
Sum of the number of coins with B and A is equal to the number of coins with G. Since, B has 5 coins A can have 3 or 4 coins and accordingly G will have 8 or 9 coins.
But G cannot have 9 coins. Thus, G has 8 coins and A has 3 coins.
The number of coins with C is the average of the number of coins with A and E. Thus, the number of coins with C is 6.
Since F has odd number of coins he should have 7 coins and D should have 4 coins.
Thus, E=9, G=8, F=7, C=6, B=5, D=4 and A=3.
Therefore, E has 9 coins
Hence, option A is the correct answer.

8) Answer (C)

The number of coins with B is a prime number, but it is not 3. Thus, the number of coins with B can be either 5 or 7.
3 people have more number of coins than B, but less than E. This is possible only when B has 5 coins and E has 9 coins.
Sum of the number of coins with B and A is equal to the number of coins with G. Since, B has 5 coins A can have 3 or 4 coins and accordingly G will have 8 or 9 coins.
But G cannot have 9 coins. Thus, G has 8 coins and A has 3 coins.
The number of coins with C is the average of the number of coins with A and E. Thus, the number of coins with C is 6.
Since F has odd number of coins he should have 7 coins and D should have 4 coins.
Thus, E=9, G=8, F=7, C=6, B=5, D=4 and A=3.
As can be observed, A, B, F and E each has odd number of coins whereas D has even number of coins.
Thus, D is the odd man out.
Hence, option C is the correct answer.

9) Answer (E)

The number of coins with B is a prime number, but it is not 3. Thus, the number of coins with B can be either 5 or 7.
3 people have more number of coins than B, but less than E. This is possible only when B has 5 coins and E has 9 coins.
Sum of the number of coins with B and A is equal to the number of coins with G. Since, B has 5 coins A can have 3 or 4 coins and accordingly G will have 8 or 9 coins.
But G cannot have 9 coins. Thus, G has 8 coins and A has 3 coins.
The number of coins with C is the average of the number of coins with A and E. Thus, the number of coins with C is 6.
Since F has odd number of coins he should have 7 coins and D should have 4 coins.
Thus, E=9, G=8, F=7, C=6, B=5, D=4 and A=3.
Thus, the required difference = 7-4 = 3
Hence, option E is the correct answer.

10) Answer (A)

S is the shortest.
3 people are taller than U but shorter than T and R is not one of them. Thus, T and U can be 2nd and 6th tallest or 1st and 5th tallest.
If T and U are 1st and 5th tallest then R is 6th tallest. This is not possible as R is taller than at least 2 people.
Hence, T and U are 2nd and 6th tallest whereas R is the tallest.
P is taller than V but shorter than Q.
Hence, the heights in the decreasing order is R>T>Q>P>V>U>S.
Thus, 6 people are shorter than R.
Hence, option A is the correct answer.

11) Answer (C)

Let us fill the absolute information mentioned in the problem statement.

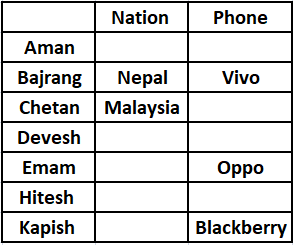
The footballer from Fiji owns a Xiaomi phone.Devesh is not from Fiji. Aman doesn’t own a Xioami or a Nokia phone. Hence, we can say that Hitesh is from Fiji and owns a Xiaomi phone.

The footballer from Korea owns a Nokia mobile. Aman doesn’t own a Xioami or a Nokia phone. Hence, we can say that Devesh is from Korea and owns a Nokia phone.

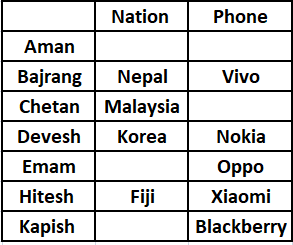
Chetan doesn’t own an Apple mobile.Hence we can say that Chetan owns a Samsung mobile and Aman owns an Apple phone. Kapish doesn’t belong to either Japan or China . Hence we can say that Kapish belongs to India. Emam is not from China hence we can say that Emam is from Japan and Aman is from China.

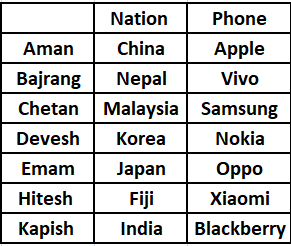
From the table, we can see that Kapish is from India. Therefore, option C is the correct answer.

12) Answer (D)

Let us fill the absolute information mentioned in the problem statement.

The footballer from Fiji owns a Xiaomi phone.Devesh is not from Fiji. Aman doesn’t own a Xioami or a Nokia phone. Hence, we can say that Hitesh is from Fiji and owns a Xiaomi phone.

The footballer from Korea owns a Nokia mobile. Aman doesn’t own a Xioami or a Nokia phone. Hence, we can say that Devesh is from Korea and owns a Nokia phone.

Chetan doesn’t own an Apple mobile.Hence we can say that Chetan owns a Samsung mobile and Aman owns an Apple phone. Kapish doesn’t belong to either Japan or China . Hence we can say that Kapish belongs to India. Emam is not from China hence we can say that Emam is from Japan and Aman is from China.

From the table, we can see that Aman is from China. Therefore, option D is the correct answer.

13) Answer (B)

Let us fill the absolute information mentioned in the problem statement.

The footballer from Fiji owns a Xiaomi phone.Devesh is not from Fiji. Aman doesn’t own a Xioami or a Nokia phone. Hence, we can say that Hitesh is from Fiji and owns a Xiaomi phone.

The footballer from Korea owns a Nokia mobile. Aman doesn’t own a Xioami or a Nokia phone. Hence, we can say that Devesh is from Korea and owns a Nokia phone.

Chetan doesn’t own an Apple mobile.Hence we can say that Chetan owns a Samsung mobile and Aman owns an Apple phone. Kapish doesn’t belong to either Japan or China . Hence we can say that Kapish belongs to India. Emam is not from China hence we can say that Emam is from Japan and Aman is from China.

From the table, we can see that Chetan owns a Samsung phone. Hence option B is the correct answer.

14) Answer (E)

Let us fill the absolute information mentioned in the problem statement.

The footballer from Fiji owns a Xiaomi phone.Devesh is not from Fiji. Aman doesn’t own a Xioami or a Nokia phone. Hence, we can say that Hitesh is from Fiji and owns a Xiaomi phone.

The footballer from Korea owns a Nokia mobile. Aman doesn’t own a Xioami or a Nokia phone. Hence, we can say that Devesh is from Korea and owns a Nokia phone.

Chetan doesn’t own an Apple mobile.Hence we can say that Chetan owns a Samsung mobile and Aman owns an Apple phone. Kapish doesn’t belong to either Japan or China . Hence we can say that Kapish belongs to India. Emam is not from China hence we can say that Emam is from Japan and Aman is from China.

From the table, we can see that all combinations are correct. Hence option E is the correct answer.

15) Answer (D)

Let us fill the absolute information mentioned in the problem statement.

The footballer from Fiji owns a Xiaomi phone.Devesh is not from Fiji. Aman doesn’t own a Xioami or a Nokia phone. Hence, we can say that Hitesh is from Fiji and owns a Xiaomi phone.

The footballer from Korea owns a Nokia mobile. Aman doesn’t own a Xioami or a Nokia phone. Hence, we can say that Devesh is from Korea and owns a Nokia phone.

Chetan doesn’t own an Apple mobile.Hence we can say that Chetan owns a Samsung mobile and Aman owns an Apple phone. Kapish doesn’t belong to either Japan or China . Hence we can say that Kapish belongs to India. Emam is not from China hence we can say that Emam is from Japan and Aman is from China.

From the table, we can see that Aman owns an Apple phone. Hence option D is the correct answer.

16) Answer (D)

1) Virat likes Amir and lives in the least numbered room.
2) The player who lives in the highest numbered room does not like Armani or Sebastian.
3) Yuvi likes Lee as well as Armani.
4) The one who likes Sebastian lives in a higher numbered room than the person who likes Azzaro.
5) The one who likes Rabada also likes Davidoff and lives in an even-numbered room.
6) Rahane lives in an odd-numbered room and likes Guerlain.
7) Dhoni likes Boult and lives in a room whose number is one greater the player who likes Davidoff.

Let us fill the direct info given in the problem statement.

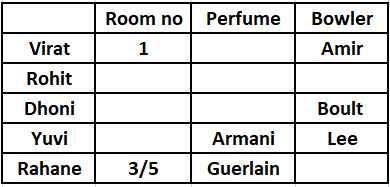
5) The one who likes Rabada also likes Davidoff and lives in an even-numbered room. This is only possible when Rohit likes Rabada as well as Davidoff . Also he lives in either room no. 2 or 4. Consequently we can say that Rahane likes Steyn.

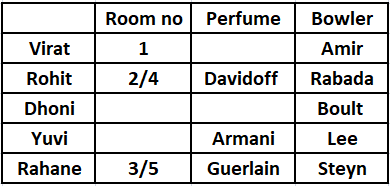
The one who likes Sebastian lives in a higher numbered room than the person who likes Azzaro. Hence, we can say that Virat don’t like Sebastian as he lives in the least number room hence we can say that Dhoni likes Sebastian and Virat likes Azzaro.

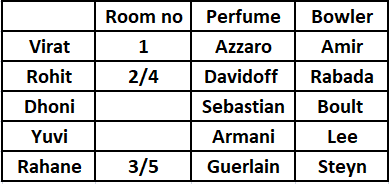
Dhoni lives in a room whose number is one greater the player who likes Davidoff. Hence, Dhoni can live in room no 3 or 5. But it is given that the player who lives in the highest numbered room does not like Armani or Sebastian. Therefore we can conclude that Dhoni lives in room no 3. Consequently we can say that Rahane, Rohit and Yuvi live in room no 5, 2 and 4 respectively.

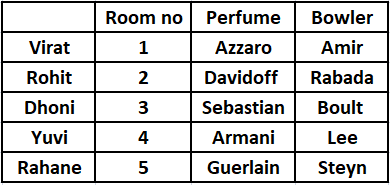
From the table, we can see that Yuvi likes Lee and he lives in room no 4. Therefore, option D is the correct answer.

17) Answer (B)

Let us fill the direct info given in the problem statement.

5) The one who likes Rabada also likes Davidoff and lives in an even-numbered room. This is only possible when Rohit likes Rabada as well as Davidoff . Also he lives in either room no. 2 or 4. Consequently we can say that Rahane likes Steyn.

The one who likes Sebastian lives in a higher numbered room than the person who likes Azzaro. Hence, we can say that Virat don’t like Sebastian as he lives in the least number room hence we can say that Dhoni likes Sebastian and Virat likes Azzaro.

Dhoni lives in a room whose number is one greater the player who likes Davidoff. Hence, Dhoni can live in room no 3 or 5. But it is given that the player who lives in the highest numbered room does not like Armani or Sebastian. Therefore we can conclude that Dhoni lives in room no 3. Consequently we can say that Rahane, Rohit and Yuvi live in room no 5, 2 and 4 respectively.

From the table, we can see that Rohit likes Davidoff perfume. Therefore, option B is the correct answer.

18) Answer (C)

Let us fill the direct info given in the problem statement.

5) The one who likes Rabada also likes Davidoff and lives in an even-numbered room. This is only possible when Rohit likes Rabada as well as Davidoff . Also he lives in either room no. 2 or 4. Consequently we can say that Rahane likes Steyn.

The one who likes Sebastian lives in a higher numbered room than the person who likes Azzaro. Hence, we can say that Virat don’t like Sebastian as he lives in the least number room hence we can say that Dhoni likes Sebastian and Virat likes Azzaro.

Dhoni lives in a room whose number is one greater the player who likes Davidoff. Hence, Dhoni can live in room no 3 or 5. But it is given that the player who lives in the highest numbered room does not like Armani or Sebastian. Therefore we can conclude that Dhoni lives in room no 3. Consequently we can say that Rahane, Rohit and Yuvi live in room no 5, 2 and 4 respectively.

From the table, we can see that Dhoni likes Sebastian. Hence option C is the correct answer.

19) Answer (E)

Let us fill the direct info given in the problem statement.

5) The one who likes Rabada also likes Davidoff and lives in an even-numbered room. This is only possible when Rohit likes Rabada as well as Davidoff . Also he lives in either room no. 2 or 4. Consequently we can say that Rahane likes Steyn.

The one who likes Sebastian lives in a higher numbered room than the person who likes Azzaro. Hence, we can say that Virat don’t like Sebastian as he lives in the least number room hence we can say that Dhoni likes Sebastian and Virat likes Azzaro.

Dhoni lives in a room whose number is one greater the player who likes Davidoff. Hence, Dhoni can live in room no 3 or 5. But it is given that the player who lives in the highest numbered room does not like Armani or Sebastian. Therefore we can conclude that Dhoni lives in room no 3. Consequently we can say that Rahane, Rohit and Yuvi live in room no 5, 2 and 4 respectively.

From the table, we can see that Rahane likes Steyn. Hence option E is the correct answer.

20) Answer (A)

Let us fill the direct info given in the problem statement.

5) The one who likes Rabada also likes Davidoff and lives in an even-numbered room. This is only possible when Rohit likes Rabada as well as Davidoff . Also he lives in either room no. 2 or 4. Consequently we can say that Rahane likes Steyn.

The one who likes Sebastian lives in a higher numbered room than the person who likes Azzaro. Hence, we can say that Virat don’t like Sebastian as he lives in the least number room hence we can say that Dhoni likes Sebastian and Virat likes Azzaro.

Dhoni lives in a room whose number is one greater the player who likes Davidoff. Hence, Dhoni can live in room no 3 or 5. But it is given that the player who lives in the highest numbered room does not like Armani or Sebastian. Therefore we can conclude that Dhoni lives in room no 3. Consequently we can say that Rahane, Rohit and Yuvi live in room no 5, 2 and 4 respectively.

From the table, we can see that Dhoni lives in Room no.3. Hence option A is the correct answer.

Take a free mock test for SBI PO

SBI PO Free Preparation App