SBI Clerk Previous Year Quant Questions

Download SBI Clerk Quant Previous Year Questions & Answers PDF for SBI Clerk Prelims and Mains exam. Very Important SBI Clerk Quant Previous Year questions on with solutions.

Download SBI Clerk Previous Year Quant Questions

790+ Mocks – Just Rs. 194. Use coupon: SBIDREAM70

InstructionsInstructions: In each of these questions, a number series is given. In each series, only one number is wrong. Find out the wrong number.

Question 1: 4    12    42    196    1005    6066    42511

a) 12

b) 42

c) 1005

d) 196

e) 6066

Question 2: 2    8    12    20    30    42    56

a) 8

b) 42

c) 30

d) 20

e) 12

Instructions

Study the following information carefully to answer the questions.

The teacher’s colony has 2800 members, out of which 650 members read only English newspaper. 550 members read only Hindi newspaper and 450 members read only Marathi newspaper. The number of members reading all the 3 newspaper is 100. Members reading Hindi as well as English newspaper are 200. 400 members read Hindi as well as Marathi newspaper and 300 members read English as well as Marathi newspaper.

Question 3: Find the difference between number of members reading English as well as Marathi newspaper and the number of members reading English as well as Hindi newspaper?

a) 300

b) 200

c) 100

d) 50

e) None of these

Download SBI Clerk Previous Papers PDF

Take a free mock test for SBI Clerk

Question 4: How many members read atleast 2 newspapers?

a) 600

b) 800

c) 500

d) 1000

e) None of these

Instructions

In each of the following questions a question is asked followed by three statements.You have to study the questions and all the given three statements and all the statements and decide whether any information provided in the statement are redundant and can be dispensed with while answering the questions ?

Question 5: What will be the cost of the painting the four walls of a room with length ,width and height is 5,3,8 meters respectively. The room has one window and one door.
I.Cost of painting per square meter is Rs 25
II.Area of window is 2.25 sq m which is half of the area of the door
III.Area of the room is 15 sq meter

a) I only

b) II only

c) III only

d) II or III only

e) All are required to answer the question

Question 6: The time taken by a boat to travel ‘x’ km upstream is twice the time taken by the same boat to travel ‘x’ km downstream. If speed of the boat in still water is 12 km/h, what is the speed of current ? (in km/h)

a) 3

b) 4

c) 3.5

d) 4.5

e) None of these

Question 7: A tap can empty a tank in one hour. A second tap can empty it in 30 min If both the taps operate simultaneously, how much time is needed to empty the tank ?

a) 20 min

b) 30 min

c) 40 min

d) 45 min

e) None of these

Banking Study Material – 18000 Questions

Daily Free SBI Online Tests

Question 8: A sum of money is divided among three employees A, B and C. A’s share is 10 times that of B, whose share is 6 times the share of C. If the sum of money that was divided was Rs 32,294 what is the share of B?

a) Rs 2892

b) Rs 17892

c) Rs 29820

d) Rs 482

Question 9: Three numbers are in such a way that the ratio of the first two numbers is 3 : 5 and the ratio of the second and third numbers is 4 : 1. If the sum of the three numbers is 259, then what is the second number?

a) 140

b) 120

c) 35

d) 135

Instructions

In the following question, two equations are given. You have to solve both the equations & find out the relationship between the variables:

Question 10: $10x^2-27x-28=0$
$6y^2-17y-14=0$

a) $x > y$

b) $x \geq y$

c) $x < y$

d) $x \leq y$

e) x = y or No relationship can be established

100+ Free GK Tests

Question 11: $6x^2-5x+1=0$
$y^2-7y+12=0$

a) $x > y$

b) $x \geq y$

c) $x < y$

d) $x \leq y$

e) x = y or No relationship can be established

Question 12: Mehul sold an item for Rs. 5.025 and incurred a loss of 25% At what price should he have sold the item to have gained a profit of 25% ?

a) Rs. 8.375

b) Rs. 10,500

c) Rs. 8,250

d) Cannot be determined

e) None of these

Question 13: The cost price of an item is two-third of its selling price. What is the gain/loss percent on that item?

a) 45

b) 50

c) 35

d) 54

e) None of these

Question 14: A bag contains 16 eggs out of which 5 are rotten. The remaining eggs are in good condition. If two eggs are drawn randomly, what is the probability that exactly one of the eggs drawn is rotten ?

a) $\frac{11}{24}$

b) $\frac{13}{24}$

c) $\frac{65}{12}$

d) $\frac{17}{24}$

e) $\frac{7}{12}$

Question 15: In how many different ways can the letters of the word ‘MARKERS’ be arranged ?

a) 840

b) 5040

c) 2520

d) 1680

e) None of these

Question 16: What should come in the place of ? in the following series?
12, 72, 240, 600, ?

a) 1270

b) 1260

c) 1290

d) 1296

e) 1236

Instructions

What should come in the place of ? in the following series?

Question 17: 641, 643, 647, 653, 659, 661, ?

a) 663

b) 667

c) 671

d) 673

e) 669

Question 18: For the following set of equations, determine the value of x + y + z ?
x + 3y + 4z = 16
2x + 4y + 5z = 22

a) 8

b) 12

c) 6

d) 5

e) cannot be determined

Question 19: The cost of 4 pens, 5 pencils and 6 sharpener is 80 and the cost of 7 pens, 9 pencils and 11 sharpener is 143. Find the cost of 1 pen, 1 pencil and 1 sharpener?

a) 13

b) 15

c) 16

d) 17

e) cannot be determined

Instructions

The table shows the number of students who appeared in the prelims exams. Both the prelims and mains exams take place every year. Those who clear prelims exams appear in mains exam and those who clear mains exam appear in PI round.

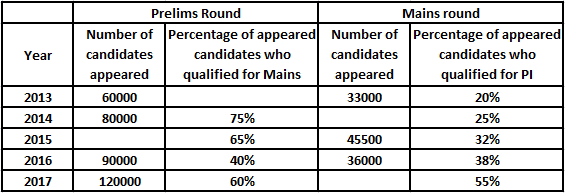
For example, in the year 2016, a total of 90000 students appeared in the prelims exam, 40% of these students cleared prelims examinations and hence, appeared in mains examination. 38% of the students who appeared in mains exams cleared the exam and hence are eligible for PI round.

 

Question 20: What is the number of students who were eligible for PI round in the year 2014?

a) 12000

b) 20000

c) 15000

d) 25000

e) 30000

General Knowledge Questions & Answers PDF

Answers & Solutions:

1) Answer (B)

(4 x 2) + 2² = 12
(12 x 3) + 3² = 45 ≠ 42
(45 x 4) + 4² = 196
(196 x 5) + 5² = 1005
(1005 x 6) + 6² = 6066
(6066 x 7) + 7² = 42511

2) Answer (A)

2 + 4 = 6 ≠ 8
6 + 6 = 12
12 + 8 = 20
20 + 10 = 30
30 + 12 = 42
42 + 14 = 56

3) Answer (C)

According to the question,
a=650; f=550;
g=450; c=100;
b+c=200; c+e = 400;
c+d = 300
b=100, e=300 and d=200
Required difference = 300-200 = 100

4) Answer (E)

According to the question,
a=650; f=550;
g=450; c=100;
b+c=200; c+e = 400;
c+d = 300
b=100, e=300 and d=200
Number of member who read at least two newspapers
= b + c + d + e = 100 + 100 + 200 + 300 = 700

5) Answer (C)

Length = 5 m , Breadth = 3 m and Height = 8 m

To find the cost of painting the walls of the room, we should know the cost of painting and the area of door and window.

Area of 4 walls (Curved Surface Area of cuboid) = $2h(l+b)$

= $(2 \times 8)(5+3) = 16 \times 8 = 128$ $m^2$

From I & II : Cost = Rs 25 per square meter

Area of window = $2.25$ $m^2$

and Area of door = $2 \times 2.25 = 4.5$ $m^2$

Thus, area to be painted = $128 – 2.25 – 4.5 = 121.25$ $m^2$

$\therefore$ Cost of painting 4 walls = $25 \times 121.25 = Rs$ $3031.25$

Thus, statement III is redundant.

=> Ans – (C)

6) Answer (B)

REASONING

7) Answer (A)

1 minute work of tap A = $\frac{1}{60}$

1 minute work of tap B = $\frac{1}{30}$

=> (A + B)’s 1 minute work = $\frac{1}{60} + \frac{1}{30}$

= $\frac{1 + 2}{60} = \frac{3}{60}$

= $\frac{1}{20}$

$\therefore$ Time taken by (A + B) to empty the tank = 20 min

8) Answer (A)

Let the share of B be x.
So, share of A = ten times of x = 10x
Share of C = one-sixth the share of b = x/6
So, total amount = 10x + x + x/6 = 67x/6 = 32294
=> x = Rs 2892

9) Answer (A)

Multiply the first ratio by 4 and the second ratio by 5.
So, the first ratio becomes 12 : 20 and the second ratio becomes 20 : 5
So, the ratio of the three numbers is 12 : 20 : 5
Let the three numbers be 12k, 20k and 5k
Sum of the numbers = 37k
=> 37k = 259
=> k = 7
So, the second number is 20k = 20*7 = 140

10) Answer (E)

$10x^2-27x-28=0$ can be written as,
$(x-\frac{7}{2})(x+\frac{4}{5})=0$
So $x = \frac{7}{2}$ or $x = -\frac{4}{5}$
$6y^2-17y-14=0$ can be written as,
$(y+\frac{2}{3})(y-\frac{7}{2})=0$
So $y = -\frac{2}{3}$ or $y = \frac{7}{2}$
x = y or No relationship can be established
Hence, option E is the correct choice.

11) Answer (C)

$6x^2-5x+1=0$ can be written as,
$(x-\frac{1}{2})(x-\frac{1}{3})=0$
So $x = \frac{1}{2}$ or $x = \frac{1}{3}$
$y^2-7y+12=0$ can be written as,
$(y-3)(y-4)=0$
So $y = 3$ or $y = 4$
c: $x < y$
Hence, option C is the correct choice.

12) Answer (A)

Mehul Selling Price = Rs.5.025
Loss = 25%
Using S.P=C.P(1-(loss/100)) ,
We get S.P = 0.75C.P
=> C.P = Rs.6.7

Now again,
S.P=C.P(1+(profit/100))
Profit=25 % and C.P.=6.7
We get S.P = 1.25*6.7
S.P=Rs. 8.375

Option A is the right answer.

13) Answer (B)

Given that ,

Cost price (cp) = $\frac{2}{3}$ selling price(sp)

• Clearly, selling price is more than cost price. Hence it is a GAIN .
• Gain% = [(sp – cp)/ cp] * 100
• = [(sp/cp) -1] * 100
• = ($\frac{34}{3}$ – 1 ) * 100
• = 50

14) Answer (A)

Out of the 16 eggs, 5 eggs are rotten and 11 eggs are in good condition.

According to the question, out of the two eggs drawn one is rotten and the other is in good condition.

Hence, required probability = $ \frac{^5C_{1} * ^{11}C_{1}}{^{16}C_{2}} = \frac{5*11}{16*15/2} = \frac{11}{24}$

Hence, option A is the right choice.

15) Answer (C)

The word MARKERS has 7 letters in which ‘R’ comes twice.

∴ Required number of arrangements = $\frac{7!}{2!}$

= 7*6*5*4*3 = 2520

16) Answer (B)

$2^4-2^2 = 16 – 4 = 12$
$3^4-3^2 = 81-9 = 72$
$4^4 – 4^2 = 256-16 = 240$
$5^4-5^2 = 625-25=600$
$6^4 – 6^2 = 1296-36= 1260$
Therefore, option B is the right answer.

17) Answer (D)

The given series consists of prime numbers from 641.
663 is divisible by 3.
665 is divisible by 5.
667 is divisible by 23.
669 is divisible by 3.
671 is divisible by 11.
673 is the next prime number after 661. Therefore, option D is the right answer.

18) Answer (C)

x + 3y + 4z = 16
2x + 4y + 5z = 22
Subtracting both equations give
x + y + z = 6

19) Answer (D)

Let the cost of 1 pen be p, 1 pencil be q and 1 sharpener be r
Then
4p + 5q + 6r = 80
7p + 9q + 11 r = 143
Subtracting both we get
3p + 4q + 5r = 63
Subtracting this from equation 1 gives
p + q + r = 17

20) Answer (C)

In the year 2013, we are given that 33000 students appeared in mains round whereas 60000 students appeared in prelims round.

Hence, percentage of appeared candidates who qualified for mains round = $\dfrac{33000}{60000}\times 100$ = 55%

Also, number of candidates eligible for PI round = $\dfrac{20}{100}\times 33000$ = 6600. In similar way we can calculate missing data for each year. Tabulating the same

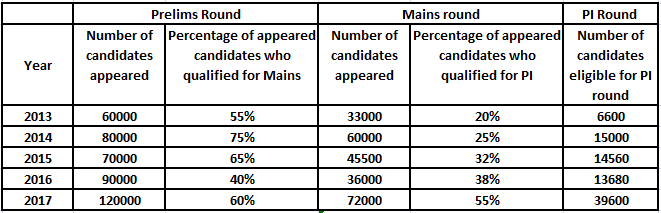
From the table, we can see that the number of students who were eligible for PI round in the year 2014 = 15000. Therefore, option C is the correct answer.

SBI Clerk Free Mock Test

SBI Free Preparation App

We hope this Simplification Question & Answers PDF of SBI Clerk is very Useful for preparation of SBI Clerk Exams.