RRB Group-D Expected Maths Questions 2019 PDF
Download Top-15 RRB Group-D Expected Maths Questions PDF. RRB GROUP-D Maths questions based on asked questions in previous exam papers very important for the Railway Group-D exam.
Download RRB Group-D Expected Maths Questions PDF
Download RRB Group-D Previous Papers PDF
Take a RRB Group-D free mock test
Question 1: A car travels 270 km in 3 hours. What is its speed?
a) 30 m/sec
b) 20 m/sec
c) 25 m/sec
d) 15 m/sec
Instructions
Question 2: Three people start to run around a circle at the same time.Time taken for them to complete a round is 15 sec,20 sec and 30 sec then after how many seconds will they meet for the 1st time ?
a) 0.8 min
b) 1 min
c) 1.5 min
d) 1.2 min
Question 3: If the roots of the quadratic equation $x^2 – 6x + 8 = 0$ are the reciprocals of the roots of another equation, which of the following is a correct representation of that equation?
a) $x^2 – 8x + 6 = 0$
b) $8x^2 – x + 6 = 0$
c) $8x^2 – 6x + 1 = 0$
d) $6x^2 – x + 8 = 0$
Take a free mock test for RRB Group-D
770 Mocks (cracku Pass) Just Rs.199
Question 4: What is the sum of the first 10 terms of the series 2, 5, 8, 11, ……?
a) 135
b) 145
c) 155
d) 165
Question 5: What is the sum of $5^2 + 6^2 + 7^2 + . . .14^2$?
a) 1015
b) 985
c) 1065
d) 2010
Question 6: A sum of money yields an interest of Rs.3920 at a compound interest of 20% per annum for first year and 30% per annum for second year. Find the sum.
a) Rs.7500
b) Rs.70000
c) Rs.4500
d) Rs.7000
RRB Group D previous year papers
Question 7: A lent a sum of Rs.50000 to B at 15% Simple Interest for 2 years. B immediately lent it to C at 15% Compound Interest compounded annually for 2 years. Find the profit of B.
a) Rs.1025
b) Rs.1500
c) Rs.1125
d) Rs.1250
Question 8: Calculate the amount(approx in Rs.) on Rs. 72000 @ 3% p.a. compounded half yearly for 2 years.
a) 74692
b) 76492
c) 76418
d) None of these
Question 9: Find the probability of forming a 8 letter word with letters A,C,G,E,I,F,D,K such that each letter is used exactly once and all the vowels come together?
a) 1/7
b) 5/56
c) 1/14
d) 3/28
Question 10: Find the probability of forming a 4 letter words out of the letter A, C, E, I, G, H, Z, W such that the first letter is W.
a) 3/8
b) 1/8
c) 3/4
d) 4/5
RRB Group-D Important Questions (download PDF)
Question 11: Positive numbers ‘a’ and ‘b’ when divided by 7 leaves a remainder of 5 and 6 respectively then what is the remainder obtained when a-b is divided by 7 if a>b ?
a) 0
b) 2
c) 4
d) 6
Question 12: Convert 379 into binary system ?
a) 100011011
b) 100111011
c) 101111011
d) 101011011
Question 13: What is the last digit of the sum of first 32 whole numbers?
a) 8
b) 6
c) 5
d) 2
Instructions
Question 14: A square having an area of 81 square meters is made into an equilateral triangle then what is the area of the triangle ?
a) 6$\sqrt{3}$
b) 12$\sqrt{3}$
c) 36$\sqrt{3}$
d) 24$\sqrt{3}$
Instructions
Question 15: Perimeter of a square is 32 and is equal to the length of the diagonal of the other square.What is the area of the other square ?
a) 128
b) 512
c) 1024
d) 256
General Science Notes for RRB Exams (PDF)
Answers & Solutions:
1) Answer (C)
Speed of the car = 270/3 = 90 km/hr
Speed of the car in m/sec = $90 \times \dfrac{5}{18} = 25$ m/sec.
2) Answer (B)
As they all start at the same time an the time after which they three meet is simply the lcm of durations of time taken=LCM of 15,20 and 30
= 60 sec
3) Answer (C)
If the roots of the quadratic equation $ax^2 + bx + c = 0$ are the reciprocals of the roots of another quadratic equation, then the other equation is given by $cx^2 + bx + a = 0$
So, option c) is the correct answer.
4) Answer (C)
2, 5, 8, 11 ….. are in AP
a = 2, d = 3
$S_n = \frac{n}{2}[2a+(n-1)d]$
$S_{10} = \frac{10}{2}[2(2)+(10-1)(3)]$
$S_{10} = 5[4+(9)(3)]$
$S_{10} = 5[31]$
$S_{10} = 155$
So the answer is option C.
5) Answer (B)
Let S1 = $1^2 + 2^2 + 3^2 + . . .14^2$ and S2 = $1^2 + 2^2 + 3^2 + 4^2$. Hence, the given series is S1 – S2.
S1=14*15*29/6 = 7*29*5 = 1015
S2 = 4*5*9/6 = 2*5*3=30.
Hence, the sum of the given series = S2 – S1 = 1015 – 30 = 985.
6) Answer (D)
Let the principal be Rs.100P
Amount at 20% per annum for 1 year = 120% of Rs.100P = Rs.120P
Amount at 30% per annum for 2nd year = 130% of Rs.120 = Rs.156P
Compound Interest = Rs.156P – Rs.100P = Rs.56P
Given, 56P = 3920
⇒ P = 70
Therefore, Principal = 100P = 100*70 = Rs.7000
7) Answer (C)
A lent Rs.50000 to B at 15% Simple Interest for 2 years.
Then, Interest = 2*15% of 50000 = 30% of 50000 = Rs.15000
B lent it to C at 15% Compound Interest for 2 years.
Amount after 2 years = 115% of 115% of 50000 = Rs.66125
Compound Interest = Rs.66125 – Rs.50000 = Rs.16125
Profit of B = Rs.16125 – Rs.15000 = Rs.1125
8) Answer (C)
Given the Principal(P) = Rs. 72,000/-
Rate of Interest (R) = 3% (compounded half yearly, n=2)
Time period(t) = 2 years
Amount on compound Interest is calculated by
$A = P(1+\frac{R/n}{100})^{nt}$
$A = 72,000(1+\frac{3/2}{100})^{2\times2}$
$A = 72,000(1+\frac{1.5}{100})^4$
$A = 72,000(1.015)^4$
$A = 76418.17$
$A$ ~ $Rs. 76418/-$
9) Answer (D)
In these letters, no letter is used more than once. So the total no. of words formed with the letters A,C,G,E,I,F,D,K is 8! Ways.
A,C,G,E,I,F,D,K
In this group A, E, I are vowels. Let us consider them as one group. This group along with the other 5 letters can be arranged in (5+1)! = 6! Ways.
Now this group contains 3 letters which can be arranged in 3! Ways
Total number of ways of arranging all the letter such that vowels come together = 3!*6!
Probability = 3!*6!/8! = 6/56 = 3/28
10) Answer (B)
Number of ways of choosing 4 letters out of 8 letters and forming words with those 4 letters =$^8C_4*4!$
Now the first letter is W, we have to choose 3 letters out of 7 letters
Number of ways of choosing 3 letters out of 7 letters =$^7C_3*3!$
Probability =$\frac{^7C_3*3!}{^8C_4*4!}$ = 1/8
11) Answer (D)
‘a’ leaves a remainder of 5 when divided by 7 so a=7x+5(let x be the quotient)
‘b’ leaves a remainder of 6 when divided by 7 so b=7y+6(let y be the quotient)
a-b=7(x-y)-1
When divided by 7 it gives -1 as remainder i.e -1+7=6
12) Answer (C)
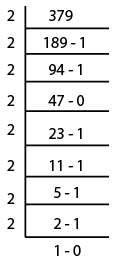
$(379)_{10} = (101111011)_2$
So the answer is option C.
13) Answer (B)
First 32 whole numbers = 0,1,2,…..31.
Sum of first 32 whole numbers = n(n+1)/2.
Here, n = 31 since the series starts with 0.
Sum = 31*32/2 = 31*16.
As we can clearly see, the last digit of the sum will be 6. Therefore, option B is the right answer.
14) Answer (C)
Area of the square $s^{2}$
$s^{2}$=81
s=9
4s=36
Triangle has 3 sides and each side has equal length as it is equilateral triangle and so a=36/3
=12
Area of an equilateral triangle=$\sqrt{3}\times a^{2}/4$
=36$\sqrt{3}$
15) Answer (B)
we have 4*s1=$\sqrt{2}$*s2
s2=32/$\sqrt{2}$
Area of a square=s2*s2
=32*32/2
=512
DOWNLOAD APP FOR RRB FREE MOCKS
We hope this Expected Maths Questions for RRB Group-D Exam will be highly useful for your preparation.





