Rhombus Questions For NMAT:
Download Rhombus Questions for NMAT PDF. Top 10 very important Rhombus Questions for NMAT based on asked questions in previous exam papers.
Download Rhombus Questions for NMAT PDF
Take NMAT mock test
Question 1: A circle is inscribed in a rhombus with diagonals 12 cm and 16 cm. The ratio of the area of circle to the area of rhombus is
a) $\frac{6\pi}{25}$
b) $\frac{5\pi}{18}$
c) $\frac{3\pi}{25}$
d) $\frac{2\pi}{15}$
Question 2: Find the area of the rhombus if the length of the line joining the midpoints of two adjacent sides is 5 cm. It is also known that the perimeter of the rhombus is 52 cm. (in cm^2)
a) 100
b) 110
c) 120
d) 130
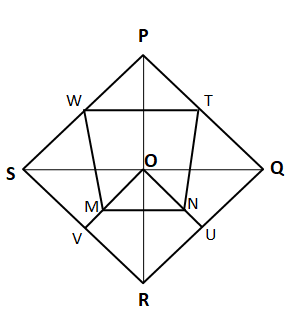
Question 3: In a rhombus PQRS, T, U, V and W are the midpoints of sides PQ, QR, RS and SP respectively. O is the point of intersection of the diagonals of the rhombus. If M and N are the mid points of OV and OU respectively, then find out the ratio of the area of pentagon MNURV to area of quadrilateral WTNM?
a) 7 : 9
b) 2 : 3
c) 5 : 6
d) 8 : 9
Question 4: If the diagonals of a rhombus of side 15 cm are in the ratio 3:4, find the area of the rhombus.
a) 54 sq. cm.
b) 108 sq. cm.
c) 144 sq. cm.
d) 200 sq. cm.
e) None of the above
Question 5: PQRS is a rhombus perimeter of 32 cm and interior angle QRS = 120°. What is the area of the rhombus PQRS?
a) 32*$\sqrt{2}$ sq.cm.
b) 16*$\sqrt{3}$ sq.cm.
c) 32*$\sqrt{3}$ sq.cm.
d) 16*$\sqrt{2}$ sq.cm.
Question 6: A person has a rectangular piece of land of dimensions 40 m x 50 m. He wants to construct a fence in the shape of a rhombus such that the area enclosed is maximum. Find the total length of the fence in metres.
a) 161
b) 160
c) 164
d) 162
Question 7: Find the area of the rhombus if the length of the line joining the mid points of two adjacent sides is 7 cm. It is also known that the perimeter of the rhombus is 100 cm. (in cm^2)
Question 8: A closed barn ABCD in the shape of a Rhombus is situated inside a vast field. Each side of the barn is equal to 10m and angle A = 60 degrees. A cow is tied to point A outside the barn with a rope of length 20m. Find the area of the field that the cow can graze.
Assume that the cow can’t enter any part of the barn.
a) $\frac{1150}{3}\pi$
b) $\frac{1200}{3}\pi$
c) $\frac{1050}{3}\pi$
d) $\frac{1100}{3}\pi$
Question 9: A circle is inscribed in a rhombus whose side is 14 cm and one of the angles is 60 degrees. Find the area of the circle.
a) 182.25 $cm^2$
b) 115.5 $cm^2$
c) 196 $cm^2$
d) 192.25 $cm^2$
Question 10: A rhombus and a square have the same perimeter, but the area of the rhombus is 4% less than the area of the square. What is the ratio of the longer diagonal of the rhombus to the shorter diagonal of the rhombus?
a) 3:1
b) 4:3
c) 3:2
d) 5:1
Join 9K MBA Aspirants Telegram Group
Take 3 Free CAT mocks (with Video solutions)
Answers & Solutions:
1) Answer (A)
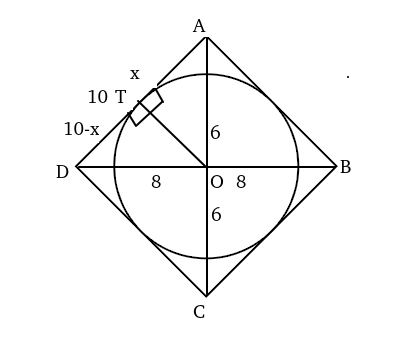
Let the length of radius be ‘r’.
From the above diagram,
$x^2+r^2=6^2\ $….(i)
$\left(10-x\right)^2+r^2=8^2\ $—-(ii)
Subtracting (i) from (ii), we get:
x=3.6 => $r^2=36-\left(3.6\right)^2$ ==> $r^2=36-\left(3.6\right)^2\ =23.04$.
Area of circle = $\pi\ r^2=23.04\pi\ $
Area of rhombus= 1/2*d1*d2=1/2*12*16=96.
.’. Ratio of areas = 23.04$\pi\ $/96=$\frac{6\pi}{25}$
2) Answer (C)
Consider the below figure
_xyDIoxi.png)
Given EF = 5 cm
According to the midpoint theorem, DB = 2*EF
DB = 10 cm
Given perimeter = 52 cm
==> DC = 52/4 = 13 cm
And DO = 5 cm
Since, $DC^2=CO^2+DO^2$
==> CO = 12 cm
Area of rhombus ABCD = 4*Area of triangle DOC = $4\cdot\frac{1}{2}\cdot5\cdot12\ =\ 120\ cm^2$
3) Answer (A)
Let us draw the diagram first,
Let us assume that length of SQ and PR be ‘$a$’ and ‘$b$’ units respectively.
Therefore the area of $\triangle$OUR = $\dfrac{\text{Area of triangle OQR}}{2}$ = $\dfrac{1}{2}*\dfrac{1}{2}*\dfrac{a}{2}*\dfrac{b}{2}$ = $\dfrac{ab}{16}$
the area of $\triangle$SQR = $\dfrac{1}{2} * SQ * OR$ = $\dfrac{1}{2} * a * \dfrac{b}{2} = \dfrac{a*b}{4}$
From the symmetry we can see that Area of $\triangle$VUR = $\dfrac{1}{2}$*$\triangle$ORQ = $\dfrac{1}{4}$*$\triangle$SQR
Hence the area of $\triangle$VUR = $\dfrac{a*b}{16}$
Area of rhombus OURV = 2*area of $\triangle$OUR = $\dfrac{a*b}{8}$
Area of $\triangle$OVU = $\dfrac{a*b}{8} – \dfrac{a*b}{16}$ = $\dfrac{a*b}{16}$
Since M and N are the mid points of OV and OU hence, Area of $\triangle$OMN = $\dfrac{1}{4}$*$\triangle$OVU = $\dfrac{a*b}{64}$
Hence, the area of the pentagon MNURV = Area of rhombus OURV – Area of triangle OMN = $\dfrac{a*b}{8}$-$\dfrac{a*b}{64}$ = $\dfrac{7ab}{64}$.
We can see that quadrilateral WTNM are trapezium.
Height of the trapezium WTNM = $\dfrac{b}{4}$ + $\dfrac{b}{8}$ = $\dfrac{3b}{8}$
Therefore, the area of trapezium WTNM = $\dfrac{1}{2}*(WT + MN)*\dfrac{3b}{8}$ = $\dfrac{1}{2}*(\dfrac{a}{2} + \dfrac{a}{4})*\dfrac{3b}{8}$ = $\dfrac{9ab}{64}$
Hence, the ratio of the area of pentagon MNURV to area of quadrilateral WTNM = $\dfrac{7ab}{64}$ : $\dfrac{9ab}{64}$ = $7 : 9$
Thus, option A is the correct answer.
4) Answer (E)
It is given that the length of the diagonals are in 3:4. Let ‘3x’, and ‘4x’ be the lengths of semi-diagonals as shown in the figure. We know that diagonals of a rhombus intersect each other perpendicularly.
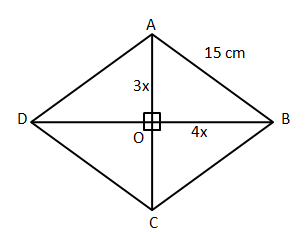
In right angle triangle AOB,
$AB^2=AO^2+BO^2$
$\Rightarrow$ $AB= \sqrt{AO^2+BO^2}$
$\Rightarrow$ $AB= \sqrt{(3x)^2+(4x)^2}$
$\Rightarrow$ $15= 5x$
$\Rightarrow$ $x= 3$cm.
Therefore, we can say that the length of diagonals = 6x and 8x or 18 and 24 cm.
Hence, the area of the rhombus = $\dfrac{1}{2}*18*24$ = 216 cm$^2$. Therefore, option E is the correct answer.
5) Answer (C)
Consider following diagram –
Side of rhombus = 32/4 = 8 cm
In a rhombus adjacent angles are supplementary.
Since angle QRS = 120°, angle PSR = 60°
Thus, triangle PSR is an equilateral triangle.
So area of triangle PSR = $ \frac{\sqrt{3}}{4}*8^2$ = 16*$\sqrt{3}$
Area of rhombus = 2 * area of triangle PSR = 32*$\sqrt{3}$ sq.cm.
Hence, option C is the correct choice.
6) Answer (C)
Let ABCD be the given rectangle and ANCO be the rhombus with the maximum area enclosed.
50 – x is the side of the rhombus.
In triangle, ADO
$(50-x)^2 = 40^2 + x^2$
$100x = 900$
$ x = 9$
Therefore, side of the rhombus = 50 – 9 = 41
Perimeter = 41 * 4 = 164
Option C
7) Answer: 336
Consider the below figure
Given EF = 7 cm
According to the midpoint theorem, DB = 2*EF
DB = 14 cm
Given perimeter = 100 cm
==> DC = 100/4 = 25 cm
And DO = 7 cm
Since, $DC^2 = CO^2 + DO^2$
==> CO = 24 cm
Area of rhombus ABCD = 4*Area of triangle DOC = $4* \frac{1}{2} * 7*24$ = 336 cm^2
8) Answer (D)
The cow can graze the whole area of a circle of radius 20m if the barn wasn’t there. Because the barn is there it can graze 300 degrees angle out of 360 degrees because 60 degrees is cut by the barn at the vertex A. This means it can graze $\frac{5}{6}$th of the area of the circle of radius 20m. This is shown by the grey area of the circle.
This area = $\frac{5}{6}\times\pi\times20^2=\frac{1000\pi}{3}$.
It can also graze two sectors of circles centered at B and D of radius 10m and angle 60 degrees. These are shown by the red areas of the circle.
This area = $2\times(\frac{1}{6}\times\pi\times10^2)=\frac{100\pi}{3}$
Total area = $\frac{1000\pi}{3}+\frac{100\pi}{3}=\frac{1100\pi}{3}$
9) Answer (B)
In triangle AOH
tan 60 = r / x ==> x = $r / \sqrt3$
Similarly in triangle COH
tan 60 = y / r ==> y = r $\sqrt3$
==> x+y = side of the rhombus = 14
==> $r / \sqrt3$ + r $\sqrt3$ = 14 ==> r = 7$\sqrt3$/2
Therefore area of the circle = pi * $r^{2}$ = $\frac{22}{7} * \frac{7\sqrt{3}}{2}*\frac{7\sqrt{3}}{2}$ = 115.5
So the correct option to choose is B – 115.5 $cm^{2}$
10) Answer (B)
Let the length of the two diagonals of the rhombus be 2X and 2Y.
So, each side of the rhombus has length $\sqrt{X^2+Y^2}$.
Area of the square with side $\sqrt{X^2+Y^2}$. is $X^2+Y^2$.
Area of the Rhombus = $1/2 * 2X * 2Y $
Hence we have $2XY = .96 *({X^2+Y^2})$.
=> $200 XY = 96X^2 + 96Y^2$
=> $12X^2 – 25XY + 12X^2$ = 0
=> $(3X – 4Y)(4X – 3Y) = 0$
=> X:Y = 3:4 or 4:3
So,the required answer is 4:3
We hope this Rhombus Questions for NMAT pdf for NMAT exam will be highly useful for your Preparation.
