Mixture and Alligation Questions for SSC-CGL Set-3 PDF
Download SSC-CGL Mixtures and Alligations Questions with answers PDF based on previous papers very useful for SSC-CGL exams. Very important Mixtures and Alligations questions for SSC exams.
Download Mixture and Alligation Questions PDF
Get 790+ mocks for Rs. 150 – Coupon PAYPAL
Question 1: The ratio of the quantities on acid and water in a mixture is 1 : 3. If 5 liters of acid is further added to the mixture, the new ratio becomes 1: 2. The quantity of new mixture in liters is
a) 32
b) 40
c) 42
d) 45
Question 2: The ratio of the volumes of water and glycerine in 240cc of a mixture is 1:3. The quantity of water (in cc that should be added to the mixture so that the new ratio of the volume of water and glycerine becomes 2:3 is
a) 55
b) 60
c) 62.5
d) 64
Question 3: Two equal vessels are filled with the mixture of water and milk in the ratio of 3:4 and 5:3 respectively. If the mixtures are poured into a third vessel, the ratio of water and milk in the third vessel will be
a) 15:12
b) 53:59
c) 20:9
d) 59:53
Question 4: The ratio of milk and water in mixtures of four containers are 5:3, 2:1, 3:2 and 7:4 respectively. In which container is the quantity of milk, relative to water, minimum?
a) First
b) Second
c) Third
d) Fourth
Question 5: Three bottles of equal capacity have a mixture of milk and water in ratio 5 : 7, 7 : 9 and 2 : 1 respectively. These three bottles are emptied into a large bottle. What is the percentage of milk in the new mixture?
a) 49.6
b) 52.3
c) 51.2
d) 50.7
SSC CGL Previous Papers Download PDF
Question 6: Three boxes of capacity 24 kg, 36 kg and 84 kg are completely filled with three varieties of wheat A, B and C respectively. All three boxes were emptied and the three types of wheat were thoroughly mixed and the mixture was put back in the three boxes. How many kg of type A wheat would be there in the third box (in kg)?
a) 10
b) 12
c) 14
d) 16
Question 7: Three bottles of equal capacity containing a mixture of milk and water in ratio 2: 5, 3: 4 and 4: 5 respectively. These three bottles are emptied into a large bottle. What will be the ratio of milk and water respectively in the large bottle?
a) 73 : 106
b) 73 : 116
c) 73: 113
d) 73: 189
Question 8: The ratio of syrup and water in a mixture is 3: 1, then the percentage of syrup in this mixture is:
a) 25%
b) 66 $\ \frac{2}{3}$%
c) 33 $\ \frac{1}{3}$%
d) 75%
Question 9: 20 liters of a mixture contains milk and water in the ratio 3: 1. Then the amount of milk to be added to the mixture so as to have milk and water in the ratio 4:1 is
a) 6 liters
b) 5 liters
c) 4 liters
d) 7 liters
Question 10: A vessel contains 60 liters of milk. 12 liters of milk taken out from it and replaced by water. Then again from the mixture, 12 liters are again taken out and replaced by water. The ratio of milk and water in the resultant mixture is:
a) 16 : 10
b) 9 : 5
c) 15 : 10
d) 16 : 9
Question 11: A mixture contains milk and water in the ratio 5 : 1. On adding 5 liters of water, the ratio of milk and water becomes 5 : 2. The quantity of milk in the mixture is
a) 25 liters
b) 16 liters
c) 22.75 liters
d) 32.5 liters
Question 12: Two vessels contain a mixture of petrol and kerosene in the ratio 4 : 3 and 3 : 5 respectively. The ratio of the volumes of the quantities from the two vessels to be mixed together so that the new mixture may contain the same volume of petrol and kerosene is
a) 9 : 6
b) 8 : 2
c) 7 : 8
d) 7 : 4
Question 13: In a mixture, sugar and milk are in the ratio 4 : 5. If 7 litres of milk is added to it, then the ratio of sugar and milk in the new mixture becomes 2 : 3. What is the total quantity (In litres) of sugar in new mixture?
a) 35
b) 28
c) 42
d) 24
Question 14: In 250 litres mixture of soda and water the ratio of amount of soda to that of water is 7 : 18. In order to make this ratio 2 : 3, how many more litres of soda should be added?
a) 37.5
b) 42.5
c) 45
d) 50
Question 15: A mixture contains acid and water in the ratio of 7 : 3. If 4 litres of water is added to it, then the ratio of acid and water becomes 7 : 4. What is the quantity (in litres) of acid in the mixture?
a) 28
b) 22
c) 20
d) 32
18000+ Questions – Free SSC Study Material
Answers & Solutions:
1) Answer (D)
Let’ say previously mixture has $x$ acid and $3x$ water.
So after adding 5 liters of acid ratio will be $(x+5)$ : $3x$ = 1:2
After solving for $x$ , we will get its value as 10
So new values will be 15 and 30 , total will be 45
2) Answer (B)
Let’s say we added $x$ cc of water.
According to previous ratio amount of water in mixture is $240 \times \frac{1}{4}$ = 60
So after adding amount of water = $60+x$
amount of glycerine = $240 \times \frac{3}{4} = 180$
Hence new ratio will be = $\frac{60+x}{180} = \frac{2}{3}$
or $x$ will be 60.
3) Answer (D)
Let’s say amounts in first vessel are 3x and 4x
in second vessel = 5y and 3y
So 7x = 8y (given) (eq. (1))
Pouring them together , new amounts will be 3x+5y and 4x+3y
so new ratio will be $\frac{3x+5y}{4x+3y}$ (eq. 2)
putting ratio of x and y from eq. (1) in eq. (2) and solving we will get new ratio as 59:53
4) Answer (C)
In first container quantity of milk relative to water is $\frac{5}{3} \times100$ = 166.65%
In second container quantity of milk relative to water is $\frac{2}{1} \times100$ = 200%
In third container quantity of milk relative to water is $\frac{2}{1} \times100$ = 150%
In fourth container quantity of milk relative to water is $\frac{7}{4} \times100$ = 175%
hence third container has least ratio
5) Answer (D)
Let the capacity of each bottle = 48 litres [L.C.M.(12,16,3)]
Ratio of milk and water in the three bottles respectively = 5:7 , 7:9 , 2:1
Milk in 1st bottle = $\frac{5}{(5+7)}\times48=20$ litres
and water in 1st bottle = $48-20=28$ litres
Similarly, milk in 2nd bottle = $\frac{7}{16}\times48=21$ litres
and water in 2nd bottle = $48-21=27$ litres
Similarly, milk in 3rd bottle = $32$ litres and water = $16$ litres
=> Total milk = $20+21+32=73$ litres
and total water = $28+27+16=71$ litres
$\therefore$ Percentage of milk in the new mixture = $\frac{73}{(73+71)}\times100$
= $\frac{7300}{144}=50.69 \approx 50.7\%$
=> Ans – (D)
6) Answer (C)
Capacity of box containing wheat A = 24 kg , B = 36 kg and C = 84 kg
Ratio of weights of boxes containing wheats A, B and C = 24 : 36 : 84 = 2 : 3 : 7
=> Quantity of type A wheat in third box = $\frac{2}{(2+3+7)}\times84$
= $\frac{84}{6}=14$ kg
=> Ans – (C)
7) Answer (B)
Let the capacity of each bottle = 63 litres [L.C.M.(7,7,9)]
Ratio of milk and water in the three bottles respectively = 2:5 , 3:4 and 4:5
Milk in 1st bottle = $\frac{2}{(2+5)}\times63=18$ litres
and water in 1st bottle = $63-18=45$ litres
Similarly, milk in 2nd bottle = $\frac{3}{7}\times63=27$ litres
and water in 2nd bottle = $63-27=36$ litres
Similarly, milk in 3rd bottle = $28$ litres and water = $35$ litres
=> Total milk = $18+27+28=73$ litres
and total water = $45+36+35=116$ litres
$\therefore$ Required ratio = $\frac{73}{116}$
=> Ans – (B)
8) Answer (A)
Ratio of syrup and water in a mixture = 3 : 1
=> Percentage of syrup in this mixture = $\frac{1}{(3+1)}\times100$
= $\frac{100}{4}=25\%$
=> Ans – (A)
9) Answer (B)
Ratio of milk and water in 20 litres mixture = 3:1
=> Quantity of milk = $\frac{3}{(3+1)}\times20=15$ litres
=> Quantity of water = $20-15=5$ litres
Let amount of milk added = $x$ litres
According to ques,
=> $\frac{15+x}{5}=\frac{4}{1}$
=> $15+x=20$
=> $x=20-15=5$
$\therefore$ The amount of milk to be added to the mixture so as to have milk and water in the ratio 4 :1 = 5 litres
=> Ans – (B)
10) Answer (D)
Initial quantity of milk = 60 litres
When 12 liters of milk taken out from it and replaced by water, then quantity of milk = $60-12=48$ litres and water = $12$ litres
(Total mixture still remains 60 litres)
Again, 12 litres of mixture is taken out, => Fraction of mixture taken out = $\frac{12}{60}=\frac{1}{5}^{th}$
=> Milk left = $48-(\frac{1}{5}\times48)=38.4$ litres
=> Water left = $60-38.4=21.6$ litres
$\therefore$ Required ratio = $\frac{38.4}{21.6}=\frac{64}{36}=16:9$
=> Ans – (D)
11) Answer (A)
Let quantity of water in mixture = $x$ litres, => Quantity of milk = $5x$ litres
According to ques, => $\frac{5x}{x+5}=\frac{5}{2}$
=> $\frac{x}{x+5}=\frac{1}{2}$
=> $2x=x+5$
=> $2x-x=5$
=> $x=5$
$\therefore$ Quantity of milk = $5\times5=25$ litres
=> Ans – (A)
12) Answer (D)
Ratio of petrol and whole mixture in 1st vessel = $\frac{4}{7}$
Ratio of petrol and whole mixture in 2nd vessel = $\frac{3}{8}$
Also, ratio of petrol and whole mixture in the final mixture = $\frac{1}{2}$
By alligation method,
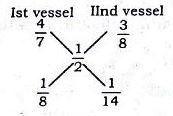
=> Petrol : Kerosene = $\frac{1}{8}:\frac{1}{14}=14:8$
= $7:4$
=> Ans – (D)
13) Answer (B)
Let quantity of milk and sugar be $4x$ and $5x$ litres respectively.
According to ques,
=> $\frac{4x}{5x+7}=\frac{2}{3}$
=> $12x=10x+14$
=> $12x-10x=2x=14$
=> $x=\frac{14}{2}=7$
$\therefore$ Total quantity of sugar = $4\times7=28$ litres
=> Ans – (B)
14) Answer (D)
Amount of soda in 250 litres mixture = $\frac{7}{(7+18)}\times250=70$ litres
=> Amount of water = $250-70=180$ litres
Let $x$ litres of soda is added.
=> $\frac{70+x}{180}=\frac{2}{3}$
=> $210+3x=360$
=> $3x=360-210=150$
=> $x=\frac{150}{3}=50$
$\therefore$ 50 litres of soda should be added.
=> Ans – (D)
15) Answer (A)
Let quantity of acid and water be $7x$ and $3x$ litres respectively.
According to ques,
=> $\frac{7x}{3x+4}=\frac{7}{4}$
=> $28x=21x+28$
=> $28x-21x=7x=28$
=> $x=\frac{28}{7}=4$
$\therefore$ Total quantity of acid = $7\times4=28$ litres
=> Ans – (A)
We hope this Mixtures and Alligations Questions PDF for SSC CGL Exam preparation is so helpful to you.





