Missing Number Questions for SSC Stenographer PDF
SSC Stenographer Missing Number Questions and Answers download PDF based on previous year question papers of SSC exam. 20 Very important Missing Number Questions for Stenographer.
Download Missing Number Questions for SSC Stenographer
10 Stenographer Mock Tests – Just Rs. 117
Download All Important SSC Stenographer Questions PDF (Topic-Wise)
SSC Stenographer Free Mock Test (Latest Pattern)
SSC Stenographer Previous Papers
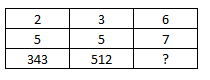
Question 1: In the following question, select the missing number from the given series.
a) 81
b) 45
c) 99
d) 28
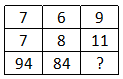
Question 2: Find the missing number as per given series in table ?
a) 10
b) 91
c) 17
d) 81
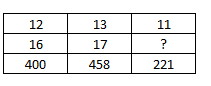
Question 3: Find the missing number as per given series ?
a) 2197
b) 729
c) 709
d) 1000
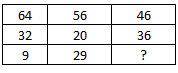
Question 4: In the following question, select the missing number from the given series.
a) 45
b) 23
c) 20
d) 51
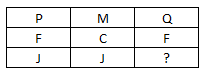
Question 5: In the following question, select the missing number from the given series
a) R
b) K
c) L
d) O
Take a free SSC Stenographer mock test
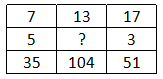
Question 6: In the following question, select the missing number from the given series.
a) 8
b) 12
c) 7
d) 9
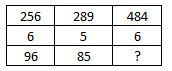
Question 7: In the following question, select the missing number form the given series
a) 124
b) 132
c) 120
d) 125
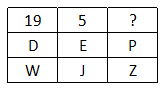
Question 8: In the following question, select the missing number from the given series.
a) 17
b) 18
c) 10
d) 9
Question 9: In the following question, select the missing number from the given series
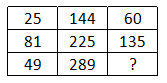
a) 119
b) 120
c) 170
d) 190
SSC STENOGRAPHER PREVIOUS PAPERS
Question 10: In the following question, select the missing number from the given series.

a) 47
b) 49
c) 50
d) 57
Question 11: In the following questions select the missing number from the given series.

a) 81
b) 361
c) 289
d) 225
Question 12: In the following question select the missing number of the given series
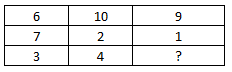
a) 9
b) 8
c) 6
d) 7
Download SSC Stenographer Previous Papers PDF
Answers & Solutions:
1) Answer (C)
In each column, the number at the end is reverse of the product of other two.
Eg :- $7\times7=49\equiv94$
$6\times8=48\equiv84$
Similarly, $9\times11=99\equiv99$
=> Ans – (C)
2) Answer (A)
In each column, the number at the end is obtained by adding the squares of other two numbers.
Eg :- $(12)^2+(16)^2=144+256=400$
$(13)^2+(17)^2=169+289=458$
Similarly, $(11)^2+(x)^2=221$
=> $x^2=221-121=100$
=> $x=\sqrt{100}=10$
=> Ans – (A)
3) Answer (A)
The number at the end in each column is the cube of the sum of other two numbers.
Eg :- $(5+2)^3=(7)^3=343$
$(3+5)^3=(8)^3=512$
Similarly, $(6+7)^3=(13)^3=2197$
=> Ans – (A)
4) Answer (B)
The sum of each column is same.
Eg :- $64+32+9=105$
and $56+20+29=105$
Similarly, $46+36+x=105$
=> $x=105-82=23$
=> Ans – (B)
5) Answer (B)
The pattern followed is that the alphabets are numbered alphabetically, A=1, B=2, C=3 and so on and then the first alphabet in each column is obtained by :
F=6 and J=10, => $6+10=16\equiv P$
C=3 and J=10, => $3+10=13\equiv M$
Similarly, Q=17 and F=6, => $17-6=11\equiv K$
=> Ans – (B)
6) Answer (A)
The number at the end in each column is obtained by multiplying the other two.
Eg :- $7\times5=35$ and $17\times3=51$
Similarly, $13\times x=104$
=> $x=\frac{104}{13}=8$
=> Ans – (A)
7) Answer (B)
In each column, the first number is the square of the number which is obtained, by dividing the other two.
Eg :- $(\frac{96}{6})^2=(16)^2=256$
and $(\frac{85}{5})^2=(17)^2=289$
Similarly, $(\frac{x}{6})^2=484=(22)^2$
=> $x=22\times6=132$
=> Ans – (B)
8) Answer (C)
The pattern followed is that the alphabets are numbered alphabetically, A=1, B=2, C=3 and so on and then the first number in each column is obtained by :
D=4 and W=23, => $23-4=19$
E=5 and J=10, => $10-5=5$
Similarly, P=16 and Z=26, => $26-16=10$
=> Ans – (C)
9) Answer (A)
The pattern followed is that in each row the number at the end is the square root of the product of first two.
Eg :- $\sqrt{25\times144}=\sqrt{5\times5\times12\times12}=5\times12=60$
$\sqrt{81\times225}=\sqrt{9\times9\times15\times15}=9\times15=225$
Similarly, $\sqrt{49\times289}=\sqrt{7\times7\times17\times17}=7\times17=119$
=> Ans – (A)
10) Answer (B)
The pattern followed is that the numbers at the corresponding edges are squares of consecutive natural numbers.
Eg :- Top left : $(1)^2=1,(2)^2=4,(3)^2=9$
Top right : $(2)^2=4,(3)^2=9,(4)^2=16$
Similarly, $(5)^2=25,(6)^2=36,(7)^2=49$
Thus, missing term = 49
=> Ans – (B)
11) Answer (D)
In each row, the number in the middle is the square of the first number.
Eg :- $13^2=169$ and $12^2=144$
Similarly, $15^2=225$
=> Ans – (D)
12) Answer (C)
The sum of each column is same.
Eg :- $6+7+3=16$
and $10+2+4=16$
Similarly, $9+1+x=16$
=> $x=16-10=6$
=> Ans – (C)
shortlink to=”https://cracku.in/ssc-study-material” color=”green”]SSC STENOGRAPHER STUDY MATERIAL TOPIC-WISE[/shortlink]
We hope this Missing Number Questions blog will definitely help at the time of your preparation. Download the cracku app for daily test.