Mensuration Questions for IIFT PDF
Download important IIFT Mensuration Questions PDF based on previously asked questions in IIFT and other MBA exams. Practice Mensuration questions and answers for IIFT exam.
Download Mensuration Questions for IIFT PDF
Get 50% Off on IIFT & Other MBA Test Series
Download IIFT Previous Papers PDF
Question 1: In ABC, points P, Q and R are the mid-points of sides AB, BC and CA respectively. If area of ABC is 20 sq. units, find the area of PQR.
a) 10 sq. units
b) 5√3 sq. units
c) 5 sq. units
d) None of these
Question 2: The figure shows a circle of diameter AB and radius 6.5 cm. If chord CA is 5 cm long, find the area of triangle ABC.
a) 60 sq. cm
b) 30 sq. cm
c) 40 sq. cm
d) 52 sq. cm
Question 3: In the adjoining figure, points A, B, C and D lie on the circle. AD = 24 and BC = 12. What is the ratio of the area of CBE to that of ADE?
a) 1 : 4
b) 1 : 2
c) 1 : 3
d) Data insufficient
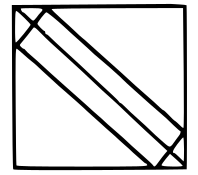
Question 4: A rectangular plank $\sqrt{10}$ metre wide, is placed symmetrically along the diagonal of a square of side 10 metres as shown in the figure. The area of the plank is:
a) $10(\sqrt{20}-1)$ sq.mt
b) $10(\sqrt{5}-1)$ sq.mt
c) $10\sqrt{20}-1$ sq.mt
d) None
Question 5: A cylinder, a Hemi-sphere and a cone stand on the same base and have the same heights. The ratio of the areas of their curved surface is:
a) $2:2:1$
b) $2:\sqrt{2}:1$
c) $\sqrt{2}:3:1$
d) None of the above
Practice IIFT Mock Tests
Question 6: A right circular cylinder has a radius of 6 and a height of 24. A rectangular solid with a square base and a height of 20, is placed in the cylinder such that each of the corners of the solid is tangent to the cylinder wall. If water is then poured into the cylinder such that it reaches the rim, the volume of water is:
a) 288(π – 5)
b) 288(2π – 3)
c) 288(3π – 5)
d) None of the above
Question 7: Radius of a spherical balloon, of radii 30 cm, increases at the rate of 2 cm per second. Then its curved surface area increases by:
a) 120π
b) 480π
c) 600π
d) None of the above
Question 8: A right circular cone is enveloping a right circular cylinder such that the base of the cylinder rests on the base of the cone. If the radius and the height of the cone is 4 cm and 10 cm respectively, then the largest possible curved surface area of the cylinder of radius r is:
a) $20πr^{2}$
b) $5πr(4 – r)$
c) $5πr(r – 4)$
d) $5πr(2 – r)$
Question 9: A spherical metal of radius 10 cm is molten and made into 1000 smaller spheres of equal sizes. In this process the surface area of the metal is increased by:
a) 1000 times
b) 100 times
c) 10 times
d) No change
e) None of the above
Question 10: Two sides of a plot measure 32 m and 24 m and the angle between them is a perfect right angle. The other two sides measure 25 m each and the other three angles are not right angles. What is the area of the plot?
a) 768 $m^2$
b) 534 $m^2$
c) 696.5 $m^2$
d) 684 $m^2$
Answers & Solutions:
1) Answer (C)
As we know, the triangle joining midpoints of sides will divide it in 4 similar traingles of equal area.
So area will be = $\frac{20}{4} = 5$
2) Answer (B)
According to given dimensions, triangle will be a right angled triangle.
So BC = 12
And area = $\frac{1}{2} \times 12 \times 5$
= 30
3) Answer (A)
As we know angles of same sectors are equal
Hence angle B and angle D will be equal. Angle BCE and angle EAD will be equal.
So triangles BCE and EAD will be similar triangles with sides ratio as 12:24 or 1:2.
Area will be in ratio of 1:4.
4) Answer (A)
In the given diagram AB=$\sqrt{10}$ m
Given that PQRS is a square and the plank is placed symmetrically $\triangle$BPA and $\triangle$AQC will be isosceles right triangles.
So PA=PB=$\frac{\sqrt{10}}{\sqrt{2}}$=$\sqrt{5}$ m
PQ= PA+AQ
AQ= PQ-PA=10-$\sqrt{5}$ m
We know that AQ=QC ($\triangle$AQC is isosceles right triangle)
So AC=$\sqrt{2}$AQ=$\sqrt{2}$*(10-$\sqrt{5}$) m
Now we can calculate area of plank
Area of ABCD= AB*AC= $\sqrt{10}$*$\sqrt{2}$(10-$\sqrt{5}$)=10($\sqrt{20}$-1) sq. mt
5) Answer (D)
The cylinder, hemisphere and cone stand on the same base and have the same height. Let the radius of the three solids be $r$ and the height be $h$.
Height of the hemisphere, $h$ = $r$ (Radius)
Curved surface area of the cylinder = $2*\pi*r*r$ = $2*\pi*r^2$
Curved surface area of the hemisphere = $2*\pi*r^2$
Curved surface area of the cone = $\pi*r*\sqrt{r^2+r^2}$ = $\pi*r*\sqrt{r^2+r^2}$ = $\pi*r^2*\sqrt{2}$
Ratio = $2:2:\sqrt{2}$ = $\sqrt{2}:\sqrt{2}:1$
As the answer is not among the given options, option D is the right answer.
6) Answer (C)
It is given that the radius of cylinder = 6 cm. The rectangular solid with a square base is placed in the cylinder such that each of the corners of the solid is tangent to the cylinder wall.
Therefore, the diagonal of square base = the diameter of circular base
Hence, a$\sqrt{2}$ = 2*6 = 12 => a = $6\sqrt{2}$ cm.
The volume of water = Volume of the cylinder – Volume of the rectangular solid
$\Rightarrow$ $\pi*6^2*24$ – $(6\sqrt{2})^2*20$
$\Rightarrow$ $864*\pi – 1440$
$\Rightarrow$ $288(3\pi – 5)$
7) Answer (B)
It is given that radius, R = 30 cm.
Curved surface area, S= $4\pi*R^2$
$\dfrac{dS}{dt}$ = $4\pi*(2R)*\dfrac{dR}{dt}$
It is given that $\dfrac{dR}{dt}$ = 2.
Hence, $\dfrac{dS}{dt}$ = $4\pi*(2*30)*2$ = $480\pi$. Hence, option B is the correct answer.
8) Answer (B)
Top face will look like the figure shown below.
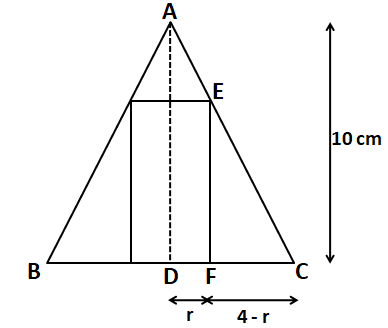
Curved surface area of the cylinder = $2*\pi*r*h$
To calculate height of the cylinder in terms of ‘r’, we can see that $\triangle$ADC is similar to $\triangle$EFC.
Therefore,
$\dfrac{AD}{DC}=\dfrac{EF}{FC}$
$\Rightarrow$ $\dfrac{10}{4} = \dfrac{h}{4-r}$
$\Rightarrow$ $h = \dfrac{5}{2}(4-r)$
Therefore, the curved surface area of the cylinder = $2*\pi*r*\dfrac{5}{2}(4-r)$ = $5πr(4 – r)$.
Hence, option B is the correct answer.
9) Answer (E)
Radius of larger sphere = $R = 10$ cm
Let radius of each of the smaller spheres = $r$ cm
=> $\frac{4}{3} \pi R^3 = 1000 \times \frac{4}{3} \pi r^3$
=> $10^3 = 1000 r^3$
=> $r = \sqrt[3]{1} = 1$ cm
Initial surface area of sphere = $4 \pi R^2 = 4 \pi \times 100 = 400 \pi$
Final surface area of 1000 spheres = $1000 \times 4 \pi r^2 = 1000 \times 4 \pi = 4000 \pi$
$\therefore$ Increase in surface area = $4000 \pi – 400 \pi = 3600 \pi$
=> $\frac{3600 \pi}{400 \pi} = 9$ times
10) Answer (D)
Length of the diagonal of the right triangle is 40.
The height of the isosceles triangle formed, with 40 as its base is 15.
So, area = (1/2 * 32 * 24) + (1/2 * 40 * 15) = 384 + 300 = 684 $m^2$
IIFT Previous year question answer PDF
We hope this Mensuration questions and answers PDF will be helpful to you.
