Geometry and Mensuration Questions for CAT PDF
Download important CAT Geometry and Mensuration Questions PDF based on previously asked questions in CAT exam. Practice geometry and Mensuration questions with solutions for CAT exam.
Download Geometry and Mensuration Questions for CAT PDF
Download CAT Quant Questions PDF
Question 1: A wooden box of thickness 0.5 cm, length 21 cm, width 11 cm and height 6 cm is painted on the inside. The expenses of painting are Rs. 70. What is the rate of painting per square centimetres?
a) Rs 0.7
b) Rs 0.5
c) Rs 0.1
d) Rs 0.2
Question 2: The figure shows a circle of diameter AB and radius 6.5 cm. If chord CA is 5 cm long, find the area of triangle ABC.

a) 60 sq. cm
b) 30 sq. cm
c) 40 sq. cm
d) 52 sq. cm
Question 3: The sum of the areas of two circles, which touch each other externally, is $153\pi$. If the sum of their radii is 15, find the ratio of the larger to the smaller radius.
a) 4
b) 2
c) 3
d) None of these
Question 4: In ABC, points P, Q and R are the mid-points of sides AB, BC and CA respectively. If area of ABC is 20 sq. units, find the area of PQR.
a) 10 sq. units
b) 5√3 sq. units
c) 5 sq. units
d) None of these
Question 5: In the adjoining figure, points A, B, C and D lie on the circle. AD = 24 and BC = 12. What is the ratio of the area of CBE to that of ADE?

a) 1 : 4
b) 1 : 2
c) 1 : 3
d) Data insufficient
Download CAT 2022 Syllabus PDF
Question 6: A rectangular plank $\sqrt{10}$ metre wide, is placed symmetrically along the diagonal of a square of side 10 metres as shown in the figure. The area of the plank is:
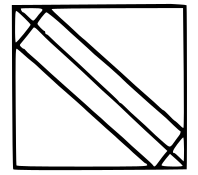
a) $10(\sqrt{20}-1)$ sq.mt
b) $10(\sqrt{5}-1)$ sq.mt
c) $10\sqrt{20}-1$ sq.mt
d) None
Question 7: A right circular cylinder has a height of 15 and a radius of 7. A rectangular solid with a height of 12 and a square base, is placed in the cylinder such that each of the corners of the solid is tangent to the cylinder wall. Liquid is then poured into the cylinder such that it reaches the rim. The volume of the liquid is
a) 147(5π-8)
b) 180(π-5)
c) 49(5π-24)
d) 49(15π-8)
Question 8: A cylinder, a Hemi-sphere and a cone stand on the same base and have the same heights. The ratio of the areas of their curved surface is:
a) $2:2:1$
b) $2:\sqrt{2}:1$
c) $\sqrt{2}:3:1$
d) None of the above
Question 9: A right circular cylinder has a radius of 6 and a height of 24. A rectangular solid with a square base and a height of 20, is placed in the cylinder such that each of the corners of the solid is tangent to the cylinder wall. If water is then poured into the cylinder such that it reaches the rim, the volume of water is:
a) 288(π – 5)
b) 288(2π – 3)
c) 288(3π – 5)
d) None of the above
Question 10: Your friend’s cap is in the shape of a right circular cone of base radius 14 cm and height 26.5 cm. The approximate area of the sheet required to make 7 such caps is
a) 6750 sq cm
b) 7280 sq cm
c) 8860 sq cm
d) 9240 sq cm
Take a free CAT online mock test
Question 11: Radius of a spherical balloon, of radii 30 cm, increases at the rate of 2 cm per second. Then its curved surface area increases by:
a) 120π
b) 480π
c) 600π
d) None of the above
Question 12: A right circular cone is enveloping a right circular cylinder such that the base of the cylinder rests on the base of the cone. If the radius and the height of the cone is 4 cm and 10 cm respectively, then the largest possible curved surface area of the cylinder of radius r is:
a) $20πr^{2}$
b) $5πr(4 – r)$
c) $5πr(r – 4)$
d) $5πr(2 – r)$
Question 13: A spherical metal of radius 10 cm is molten and made into 1000 smaller spheres of equal sizes. In this process the surface area of the metal is increased by:
a) 1000 times
b) 100 times
c) 10 times
d) No change
e) None of the above
Answers & Solutions:
1) Answer (C)
Inside dimensions of cube are as follows:
Length = $21 – 2*(0.5) = 20$
Width = $11 – 2*(0.5) = 10$
Height = $6 – 0.5 = 5.5$ (As top surface is open)
So total area painted = $2(20 \times 5.5) + 2(10 \times 5.5) + (10 \times 20)$
$= 220 + 110 + 200$
$= 530$ sq. cm.
Cost of painting 530 sq. cm. is 70
So cost per sq. cm. = $\frac{70}{530} = 0.1$ (nearly)
2) Answer (B)
According to given dimensions, triangle will be a right angled triangle.
So BC = 12
And area = $\frac{1}{2} \times 12 \times 5$
= 30
CAT Online Most Trusted Courses
3) Answer (A)
Given:
$\pi((r_1)^2 + (r_2)^2) = 153\pi$
So
$(r_1)^2 + (r_2)^2 = 153$
Or $((r_1) + (r_2))^2 – 2(r_1)(r_2) = 153$
Or $(r_1)(r_2) = 36$ and $(r_1) + (r_2) = 15$
$r_1 = 12$
$r_2 = 3$
Ratio = 4
4) Answer (C)
As we know, the triangle joining midpoints of sides will divide it in 4 similar traingles of equal area.
So area will be = $\frac{20}{4} = 5$
5) Answer (A)
As we know angles of same sectors are equal
Hence angle B and angle D will be equal. Angle BCE and angle EAD will be equal.
So triangles BCE and EAD will be similar triangles with sides ratio as 12:24 or 1:2.
Area will be in ratio of 1:4.
6) Answer (A)
In the given diagram AB=$\sqrt{10}$ m

Given that PQRS is a square and the plank is placed symmetrically $\triangle$BPA and $\triangle$AQC will be isosceles right triangles.
So PA=PB=$\frac{\sqrt{10}}{\sqrt{2}}$=$\sqrt{5}$ m
PQ= PA+AQ
AQ= PQ-PA=10-$\sqrt{5}$ m
We know that AQ=QC ($\triangle$AQC is isosceles right triangle)
So AC=$\sqrt{2}$AQ=$\sqrt{2}$*(10-$\sqrt{5}$) m
Now we can calculate area of plank
Area of ABCD= AB*AC= $\sqrt{10}$*$\sqrt{2}$(10-$\sqrt{5}$)=10($\sqrt{20}$-1) sq. mt
7) Answer (A)
Volume of liquid = Volume of cylinder – Volume of rectangular solid

Volume of cylinder = $\pi*r^{2}*h$
=$\pi*7^{2}*15$ = $735\pi$
Volume of rectangular solid = Area of square base * height
In square ABCD, AC = $\sqrt{2}$*AB so AB = $\frac{14 }{\sqrt{2}}$ = $7\sqrt{2}$
Volume of rectangular solid = Area of square base * height = $(AB)^{2}$*height = $(7\sqrt{2})^{2}*12$
= $98*12$ = $1176$
So Volume of liquid = Volume of cylinder – Volume of rectangular solid
= $735\pi$ – $1176$ = $147(5π-8)$
8) Answer (D)
The cylinder, hemisphere and cone stand on the same base and have the same height. Let the radius of the three solids be $r$ and the height be $h$.
Height of the hemisphere, $h$ = $r$ (Radius)
Curved surface area of the cylinder = $2*\pi*r*r$ = $2*\pi*r^2$
Curved surface area of the hemisphere = $2*\pi*r^2$
Curved surface area of the cone = $\pi*r*\sqrt{r^2+r^2}$ = $\pi*r*\sqrt{r^2+r^2}$ = $\pi*r^2*\sqrt{2}$
Ratio = $2:2:\sqrt{2}$ = $\sqrt{2}:\sqrt{2}:1$
As the answer is not among the given options, option D is the right answer.
9) Answer (C)
It is given that the radius of cylinder = 6 cm. The rectangular solid with a square base is placed in the cylinder such that each of the corners of the solid is tangent to the cylinder wall.
Therefore, the diagonal of square base = the diameter of circular base
Hence, a$\sqrt{2}$ = 2*6 = 12 => a = $6\sqrt{2}$ cm.
The volume of water = Volume of the cylinder – Volume of the rectangular solid
$\Rightarrow$ $\pi*6^2*24$ – $(6\sqrt{2})^2*20$
$\Rightarrow$ $864*\pi – 1440$
$\Rightarrow$ $288(3\pi – 5)$
10) Answer (D)
A cone is formed when the 2 edges of the sector of a circle are joined.
We have to find the central angle subtended to find out the area of the sheet required to make the cone.
It has been given that the height of the cone is 26.5 cm and the base radius is 14 cm.
The slant height of the cone will be equal to the radius of the sector of the circle.
Slant height = $\sqrt{26.5^2+14^2}$ = $\sqrt{898.25}$
$\sqrt{898.25}$ is very close in value to $\sqrt{900}$
Let us use $\sqrt{900}$ for the ease of calculation.
$\sqrt{900}$ = $30$ cm.
Area of sheet required to make 1 cap = Curve surface area of the cone = $(\pi)rl$ = (22/7)*14*30 =1320
Area of sheet required to make 7 cap = 7*1320 = 9240 sq cm
11) Answer (B)
It is given that radius, R = 30 cm.
Curved surface area, S= $4\pi*R^2$
$\dfrac{dS}{dt}$ = $4\pi*(2R)*\dfrac{dR}{dt}$
It is given that $\dfrac{dR}{dt}$ = 2.
Hence, $\dfrac{dS}{dt}$ = $4\pi*(2*30)*2$ = $480\pi$. Hence, option B is the correct answer.
12) Answer (B)
Top face will look like the figure shown below.
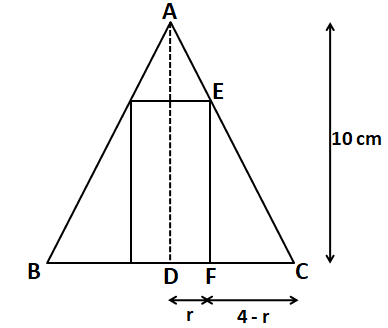
Curved surface area of the cylinder = $2*\pi*r*h$
To calculate height of the cylinder in terms of ‘r’, we can see that $\triangle$ADC is similar to $\triangle$EFC.
Therefore,
$\dfrac{AD}{DC}=\dfrac{EF}{FC}$
$\Rightarrow$ $\dfrac{10}{4} = \dfrac{h}{4-r}$
$\Rightarrow$ $h = \dfrac{5}{2}(4-r)$
Therefore, the curved surface area of the cylinder = $2*\pi*r*\dfrac{5}{2}(4-r)$ = $5πr(4 – r)$.
Hence, option B is the correct answer.
13) Answer (E)
Radius of larger sphere = $R = 10$ cm
Let radius of each of the smaller spheres = $r$ cm
=> $\frac{4}{3} \pi R^3 = 1000 \times \frac{4}{3} \pi r^3$
=> $10^3 = 1000 r^3$
=> $r = \sqrt[3]{1} = 1$ cm
Initial surface area of sphere = $4 \pi R^2 = 4 \pi \times 100 = 400 \pi$
Final surface area of 1000 spheres = $1000 \times 4 \pi r^2 = 1000 \times 4 \pi = 4000 \pi$
$\therefore$ Increase in surface area = $4000 \pi – 400 \pi = 3600 \pi$
=> $\frac{3600 \pi}{400 \pi} = 9$ times
Preparation tips for CAT – Beginners
Download Free CAT Preparation App
We hope this Geometry and Mensuration questions and answers PDF will be helpful to you.




![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)
