Maths Questions for SSC CHSL Set-3 PDF
Download SSC CHSL Maths questions with answers Set-3 PDF based on previous papers very useful for SSC CHSL Exams. Top-10 Very Important Maths Questions for SSC Exam
Download Maths Questions for SSC CHSL Set-3 PDF
Get 200 SSC mocks for just Rs. 249. Enroll here
Take a free mock test for SSC CHSL
Download SSC CHSL Previous Papers
More SSC CHSL Important Questions and Answers PDF
Question 1: A ladder is placed along a wall such that its upper end is touching the top of the wall. The foot of the ladder is 10 ft away from the wall and the ladder is making an angle of $60^{0}$ with the ground. When a man starts climbing on it, it slips and now ladder makes an angle of 30° with ground. How much did the ladder slip from the top of the wall?
a) 12 ft
b) 20 ft
c) 7.32 ft
d) 18 ft
Question 2: The sum of the ages of husband and wife at present is 100. Ten years ago the ratio of their ages was 9:7. What is the age of the husband?
a) 45 years
b) 55 years
c) 65 years
d) 40 years
Question 3: If $a^{3} + b^{3}$ = 19 and ab = -6 , then what is the value of a + b?
a) 5
b) 7
c) 1
d) -5
Question 4: Product of three consecutive odd numbers is 1287. What is the largest of the three numbers?
a) 9
b) 11
c) 13
d) 17
Question 5: Which of the following quadratic equations has real roots?
a) $3x^{2}-5x+2=0$
b) $3x^{2}-4x+2=0$
c) $4x^{2}-3x+2=0$
d) $5x^{2}-2x+2=0$
SSC CHSL Study Material (FREE Tests)
Question 6: Expand and simplify $(x + 5)^2 + (x – 3)^2$
a) $2(x^2 + 2x – 17)$
b) $2(x^2 – 2x + 17)$
c) $2(x^2 – 2x – 17)$
d) $2(x^2 + 2x + 17)$
Question 7: What is the value of $\frac{5.6 \times 0.36 + 0.42 \times 3.2}{0.8 \times 2.1}$?
a) 2
b) 1
c) 3
d) $\frac{3}{2}$
Question 8: Determine the value of m for which $4x+\frac{\sqrt{x}}{6}+\frac{m^2}{4}$ is a perfect square.
a) $\frac{1}{24}$
b) $\frac{1}{12}$
c) $12$
d) $24$
Question 9: What is the total length intercepted between both the axes by the line 8x+4y=40?
a) 5
b) 10
c) 15
d) 20
Question 10: If $2x+\frac{2}{x}=3$ than the value of $x^{3}+\frac{1}{x^{3}}+2$ is
a) 3/4
b) 4/5
c) 5/8
d) 7/8
Answers & Solutions:
1) Answer (C)
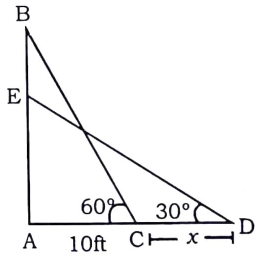
Given : BC is the initial position of the ladder, and DE is its final position. So, DE = BC (as both are the same ladders)
To find : CD = $x=?$
Solution : In $\triangle$ ABC,
=> $cos(60^\circ)=\frac{AC}{BC}$
=> $\frac{1}{2}=\frac{10}{BC}$
=> $BC=10\times2=20$
Thus, $DE=BC=20$
Similarly, in $\triangle$ ADE,
=> $cos(30^\circ)=\frac{AD}{DE}$
=> $\frac{\sqrt3}{2}=\frac{x+10}{20}$
=> $x+10=10\sqrt3$
=> $x=10(\sqrt3-1)$
=> $x=10\times0.732=7.32$
$\therefore$ The ladder slipped 7.32 ft
=> Ans – (C)
2) Answer (B)
Let husband’s age = $x$ years
=> Wife’s age = $(100 – x)$ years
According to ques,
=> $\frac{x – 10}{100 – x – 10} = \frac{9}{7}$
=> $\frac{x – 10}{90 – x} = \frac{9}{7}$
=> $7x – 70 = 810 – 9x$
=> $9x + 7x = 810 + 70 = 880$
=> $x = \frac{880}{16} = 55$ years
=> Ans – (B)
3) Answer (C)
$a^{3}+b^{3}=(a+b)^{3}-3ab(a+b)$
$19=(X)^{3}-3(-6)(X)$
$X^{3}+18X-19=0$
by option verification, only X = 1 satisfies the above equation.
so the answer is option C.
4) Answer (C)
Let the three consecutive odd numbers be $(x-2),(x),(x+2)$
=> Product = $(x-2)(x)(x+2)=1287$
=> $x(x^2-4)=11\times117$
=> $x=11$ and $x^2-4=117$
$\therefore$ Largest of the three numbers = $11+2=13$
=> Ans – (C)
5) Answer (A)
A quadratic equation : $ax^2 + bx + c = 0$ has real roots iff Discriminant, $D = b^2 – 4ac \geq 0$
(A) : $3x^{2}-5x+2=0$
=> D = $(-5)^2 – 4(3)(2) = 25 – 24 = 1$
(B) : $3x^{2}-4x+2=0$
=> D = $(-4)^2 – 4(3)(2) = 16 – 24 = -8$
(C) : $4x^{2}-3x+2=0$
=> D = $(-3)^2 – 4(4)(2) = 9 – 32 = -23$
(D) : $5x^{2}-2x+2=0$
=> D = $(-2)^2 – 4(5)(2) = 4 – 40 = -36$
Thus, the equation : $3x^{2}-5x+2=0$ has real roots.
6) Answer (D)
Expression : $(x + 5)^2 + (x – 3)^2$
= $(x^2 + 10x + 25) + (x^2 – 6x + 9)$
= $2x^2 + 4x + 34$
= $2(x^2 + 2x + 17)$
7) Answer (A)
=$\frac{5.6 \times 0.36 + 0.42 \times 3.2}{0.8 \times 2.1}$
= $\frac{2.016 + 1.3444}{1.68}$
=$\frac{3.36}{1.68}$
=2
8) Answer (B)
Expression : $4x+\frac{\sqrt{x}}{6}+\frac{m^2}{4}$
Let $\sqrt{x}=y$
= $4y^2+\frac{y}{6}+\frac{m^2}{4}$
= $(2y)^2+2(2y)(\frac{1}{24})+(\frac{m}{2})^2$
Using, $a^2+2ab+b^2=(a+b)^2$
=> $\frac{m}{2}=\frac{1}{24}$
=> $m=\frac{2}{24}=\frac{1}{12}$
=> Ans – (B)
9) Answer (C)
Equation of line = $8x+4y=40$
=> $\frac{8x}{40}+\frac{4y}{40}=1$
=> $\frac{x}{5}+\frac{y}{10}=1$
Thus, total length intercepted = $5+10=15$
=> Ans – (C)
10) Answer (D)
Expression : $2x+\frac{2}{x}=3$
=> $2(x+\frac{1}{x})=3$
=> $x+\frac{1}{x}=\frac{3}{2}$ ———(i)
Cubing both sides, we get :
=> $(x+\frac{1}{x})^3=(\frac{3}{2})^3$
=> $x^3+\frac{1}{x^3}+3.x.\frac{1}{x}(x+\frac{1}{x})=\frac{27}{8}$
Substituting value from equation (i)
=> $x^3+\frac{1}{x^3} + 3(\frac{3}{2})=\frac{27}{8}$
=> $x^3+\frac{1}{x^3}=\frac{27}{8}-\frac{9}{2}$
=> $x^3+\frac{1}{x^3}=\frac{27-36}{8}=\frac{-9}{8}$
Adding 2 on both sides, we get :
=> $x^3+\frac{1}{x^3}+2=2-\frac{9}{8}$
=> $x^3+\frac{1}{x^3}+2=\frac{7}{8}$
=> Ans – (D)
DOWNLOAD APP TO ACESSES DIRECTLY ON MOBILE
We hope this Maths questions of set-3 pdf for SSC CHSL Exam preparation is so helpful to you.





