CAT Geometry Circle Questions [Download PDF]

Geometry Circle is one of the most important topics in the CAT Quants section. If you’re weak in Geometry Circle questions for CAT, make sure you learn all the basic concepts of solving the questions and also all the important formulas. Here, you can learn all the important questions on the concept of CAT Geometry Circle. You can check out these CAT Geometry Circle questions from the CAT Previous year’s papers. This post will look at important Geometry Circle questions in the CAT quant section. These are a good source of practice for CAT preparation; If you want to practice these questions, you can download this CAT TSD Questions PDF along with the detailed solutions (and video solutions) below, which is completely Free.

Download Geometry Circle Questions for CAT

Enroll for CAT 2023 Online Course

Question 1: Two circles with centres P and Q cut each other at two distinct points A and B. The circles have the same radii and neither P nor Q falls within the intersection of the circles. What is the smallest range that includes all possible values of the angle AQP in degrees?

a) Between 0 and 90

b) Between 0 and 30

c) Between 0 and 60

d) Between 0 and 75

e) Between 0 and 45

1) Answer (C)

View Video Solution

Solution:

To know the range, we have to take the limiting case.

The limiting case in this case is when the circles pass through each other’s centers.

In this case, PQ = AP = AQ => They form an equilateral triangle => angle AQP = 60 degrees.

So, the maximum possible angle is 60 degrees.

Another limiting case is when the circles touch each other externally.

In this case, angle AQP = 0 degrees.

Hence, the range is 0 to 60.

Question 2: Two circles, both of radii 1 cm, intersect such that the circumference of each one passes through the centre of the other. What is the area (in sq. cm.) of the intersecting region?

a) $\frac{\pi}{3}-\frac{\sqrt 3}{4}$

b) $\frac{2\pi}{3}+\frac{\sqrt 3}{2}$

c) $\frac{4\pi}{3}-\frac{\sqrt 3}{2}$

d) $\frac{4\pi}{3}+\frac{\sqrt 3}{2}$

e) $\frac{2\pi}{3}-\frac{\sqrt 3}{2}$

2) Answer (E)

View Video Solution

Solution:

The circumferences of the two circle pass through each other’s centers. Hence, O1A = O1B=O1O2 = 1cm

By symmetry, the line joining the two centres would be bisect AB and would be bisected by AB. As the line joining the center to the midpoint of a chord is perpendicular to the chord, O1O2 and AB are perpendicular bisectors of each other. Suppose they intersect at point P.

O1P = Half of O1O2 = 1/2 cm
So, the angle AO1P = 60 degrees as cos 60 = 1/2
By symmetry, BO1P = 60 degrees.
So, angle AO1B= 120 degrees

In the above, the required area is 2 times A(segment ABO2)(blue region). And A(segment ABO2)(blue region) = A(sector O2AO1B)(blue + red) – A(triangleO1AB )(red)

Area of sector = 120°/360° * $\pi * 1^2 $ = $\pi/3$

Area of triangle = 1/2 * b * h = 1/2 * (2* 1 cos 30°) * (1/2) = √3/4

Hence, required area = $\frac{\pi}{3}-\frac{\sqrt 3}{4}$ . Hence so the required area is 2 times the above value which is $\frac{2\pi}{3}-\frac{\sqrt 3}{2}$

Question 3: There are two concentric circles such that the area of the outer circle is four times the area of the inner circle. Let A, B and C be three distinct points on the perimeter of the outer circle such that AB and AC are tangents to the inner circle. If the area of the outer circle is 12 square centimeters then the area (in square centimeters) of the triangle ABC would be

a) $\pi\sqrt{12}$

b) $9/\pi$

c) $9\sqrt3/\pi$

d) $6\sqrt3/\pi$

3) Answer (C)

View Video Solution

Solution:

Let R ,r be radius of big and small circles respectively. We know that R=2r.

And since area = 12 ;

$R^2 = \frac{12}{\pi}$.
$r^2$ = $\frac{3}{\pi}$

By pythagoras theorem in the small triangle with side ‘x’ we have x = $\sqrt{\ 3}r$.

Angle OAB = $\tan\ \theta\ \ =\ \ \frac{\ r}{\sqrt{\ 3}r}\ =\ 30$
Hence Angle CAB = 60.

So area = $\ \frac{\ 1}{2}\ \times\ 2\sqrt{\ 3}r\times\ 2\sqrt{\ 3}r\times\ \sin\ 60$.
On substituting the value of sin 60 and $r^2$, we get

Area = $9\sqrt3/\pi$.

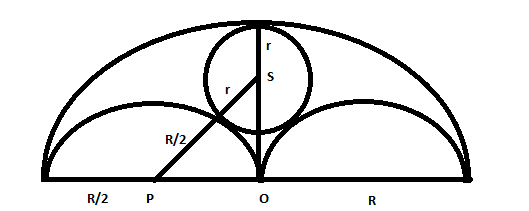
Question 4: Three horses are grazing within a semi-circular field. In the diagram given below, AB is the diameter of the semi-circular field with center at O. Horses are tied up at P, R and S such that PO and RO are the radii of semi-circles with centers at P and R respectively, and S is the center of the circle touching the two semi-circles with diameters AO and OB. The horses tied at P and R can graze within the respective semi-circles and the horse tied at S can graze within the circle centred at S. The percentage of the area of the semi-circle with diameter AB that cannot be grazed by the horses is nearest to

a) 20

b) 28

c) 36

d) 40

4) Answer (B)

View Video Solution

Solution:

Let R be radius of big circle and r be radius of circle with centre S. Radius of 2 semicircles is R/2.

From Right angled triangle OPS, using pythagoras theorem we get

$(r+0.5R)^2 = (0.5R)^2 + (R-r)^2$ . We get R=3r .

Now the area of big semicircle that cannot be grazed is Area of big S.C – area of 2 semicircle – area of small circle = $\pi*R^2$/2 – 2*$\pi*(0.5R)^2$/2-$\pi*r^2$ = $\pi*R^2$/2 – 2*$\pi*(0.5R)^2$/2-$\pi*(R/3)^2$= $\pi*R^2$/2 – $\pi*(R)^2$/4-$\pi*(R)^2$/9 = 5*$\pi*R^2$/36.  this is about 28 % of the area $\pi*R^2$/2 . Hence option B.

Question 5: In the figure below, AB is the chord of a circle with center O. AB is extended to C such that BC = OB. The straight line CO is produced to meet the circle at D. If $\angle{ACD}$ = y degrees and $\angle{AOD}$ = x degrees such that x = ky, then the value of k is

a) 3

b) 2

c) 1

d) None of the above.

5) Answer (A)

View Video Solution

Solution:

Since Angle BOC = Angle BCO = y.

Angle OBC = 180-2y .

Hence Angle ABO =  z = 2y = Angle OAB.

Now since x is exterior angle of triangle AOC .

We have x = z + y = 3y.

Hence option A.

Instructions

Directions for the following three questions: Answer the questions on the basis of the information given below

<img “=”” alt=”” class=”img-responsive” src=”https://cracku.in/media/questionGroup/Quant_I.png”/>

In the adjoining figure I and II are circles with centres P and Q respectively, The two circles touch each other and have common tangent that touches them at points R and S respectively. This common tangent meets the line joining P and Q at O. The diameters of I and II are in the ratio 4: 3. It is also known that the length of PO is 28 cm.

Question 6: What is the ratio of the length of PQ to that of QO?
[CAT 2004]

a) 1 : 4

b) 1 : 3

c) 3 : 8

d) 3 : 4

6) Answer (B)

View Video Solution

Solution:

Triangles PRO and QSO are similar.

PR/QS = 4/3.

Therefore, PO/QO = 4/3 =>

Let the radius of 2 circles be 4R and 3R respectively.

28/(28-7R) = 4/3

4-R = 3

R = 1

Required ratio of PQ/QO = (4R+3R)/(28-7R) = 7R/(28-7R) = 7/21 = 1:3

Question 7: What is the radius of the circle II?[CAT 2004]

a) 2 cm

b) 3 cm

c) 4 cm

d) 5 cm

7) Answer (B)

View Video Solution

Solution:

Let the radius of circles I and II be 4R and 3R respectively.

Triangles PRO and QSO are similar.

PR/QS = 4/3.

Therefore, PO/QO = PR/QS

=> PO/QO = 4/3

=> 28/(28-7R) = 4/3

=> 4-R = 3

=> R = 1

Radius of smaller circle = 3R = 3

Question 8: The length of SO is
[CAT 2004]

a) $8 \sqrt{3}$ cm

b) $10 \sqrt{3}$ cm

c) $12 \sqrt{3}$ cm

d) $ 14 \sqrt{3}$ cm

8) Answer (C)

View Video Solution

Solution:

Triangles PRO and QSO are similar.

PR/QS = 4/3.

Therefore, PO/QO = 4/3 =>

Let the radius of 2 circles be 4R and 3R respectively.

28/(28-7R) = 4/3

4-R = 3

R = 1

Therefore, SO = $\sqrt{21^2 – 3^2}$ = $\sqrt{432}$ = $12 \sqrt{3}$ cm

Instructions

A punching machine is used to punch a circular hole of diameter two Units from a square sheet of aluminium of width 2 units, as shown below. The hole is punched such that the circular hole touches one corner P of the square sheet and the diameter of the hole originating at P is in line with a diagonal of the square:

<img “=”” alt=”” class=”img-responsive” src=”https://cracku.in/media/questionGroup/DI_3_5.png”/>

Question 9: The proportion of the sheet area that remains after punching is:

a) ($\pi$+2)/ 8

b) (6 – $\pi$)/ 8

c) (4 – $\pi$)/4

d) ($\pi$ -2)/ 4

e) (14 -3 $\pi$)/ 6

9) Answer (B)

View Video Solution

Solution:

The area of triangle ABC is 1/2 * $\sqrt2$ * $\sqrt2$ = 1

Area of semi-circle ABC = $\pi/2$

So, area of circle outside the square = $\pi/2$ – 1 = ($\pi$ -2)/2

So, area of circle inside the sheet = $\pi$ – ($\pi/2$ – 1) = 1 + $\pi/2$

Area of original square = 2*2 = 4

So, area of the sheet after punching = 4 – 1 – $\pi/2$ = 3 – $\pi/2$

So, proportion of sheet that remains after punching = (3 – $\pi/2$)/4 = (6 – $\pi$)/8

Question 10: Find the area of the part of the circle (round punch) falling outside the square sheet.

a) $\pi$ /4

b) ($\pi$ -1)/2

c) ($\pi$ -1)/4

d) ($\pi$ -2)/2

e) ($\pi$ -2)/4

10) Answer (D)

View Video Solution

Solution:

The area of triangle ABC is 1/2 * $\sqrt2$ * $\sqrt2$ = 1
Area of semi-circle ABC = $\pi/2$
So, area of circle outside the square = $\pi/2$ – 1 = ($\pi$ -2)/2

Checkout: CAT Free Practice Questions and Videos

Question 11: A semi-circle is drawn with AB as its diameter. From C, a point on AB, a line perpendicular to AB is drawn meeting the circumference of the semi-circle at D. Given that AC = 2 cm and CD = 6 cm, the area of the semi-circle (in sq. cm) will be:

a) 32$\pi$

b) 50$\pi$

c) 40.5$\pi$

d) 81$\pi$

e) Can’t be determined

11) Answer (B)

View Video Solution

Solution:

In triangle CDO, which is a right anged triangle, we can use pythagoras theorem.

$6^2$ + $(r-2)^2$ = $r^2$

=> 36 + $r^2 – 4r + 4$ = $r^2$

=> 4r = 40

=> r = 10

=> Area = $\pi *10*10/2$ = $50\pi $

Question 12: What is the distance in cm between two parallel chords of lengths 32 cm and 24 cm in a circle of radius 20 cm?

a) 1 or 7

b) 2 or 14

c) 3 or 21

d) 4 or 28

12) Answer (D)

View Video Solution

Solution:

The distances of the chords from the center are 12 cm and 16 cm respectively.

If the chords lie on the same side of the center, the distance between the chords is 4 cm, if they lie on opposite sides of the center, the distance between them is 28 cm.

Checkout: CAT Free Practice Questions and Videos

Question 13: Two identical circles intersect so that their centers, and the points at which they intersect, form a square of side 1 cm. The area in sq. cm of the portion that is common to the two circles is

a) $\pi$/4

b) $\pi$/2-1

c) $\pi$/5

d) $\sqrt\pi-1$

13) Answer (B)

View Video Solution

Solution:

We know that quad ambn is a square of side 1.

Area of the sector a-mqn is $\frac{90}{360}* \pi *1*1$ = $\frac{\pi }{4}$.

Area of square = 1*1 = 1

Area of common portion = 2 * Area of sector – Area of square

= 2 * $\frac{\pi }{4}$ – 1 =  $\frac{\pi }{2}$ – 1

Enroll to CAT 2023 Online Coaching

Download CAT Quant Formulas PDF