IBPS PO Quantitative Aptitude Questions With Answers PDF:
Download IBPS PO Quantitative Aptitude Questions PDF
75 IBPS PO Mocks for just Rs.199
Question 1: The compound interest earned by Suresh on a certain amount at the end of two years at the rate of 8 p.c.p.a was Rs. 1,414.4. What was the total amount that Suresh got back at the end of two years in the form of principal plus interest earned?
a) Rs. 9,414.4
b) Rs. 9,914.4
c) Rs. 9,014.4
d) Rs. 8,914.4
e) None of these
Instructions: Directions for the next five questions: Study the following table carefully to answer the questions. Rate of interest (pcpa) offered by five companies on deposits under different schemes
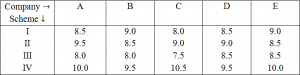
Question 2: Mr. X deposited an amount in Scheme II with company C for two years. After that he withdrew the amount and reinvested only the principal amount in scheme IV of Company B for two years. Total amount of simple interest accrued from the two schemes is Rs. 14800. What was the principal amount?
a) Rs. 48000
b) Rs. 42000
c) Rs. 40000
d) Can’t be determined
e) None of these
Question 3: Company E offers compound interest under Scheme I and Company A offers simple interest under scheme IV. What will be the difference between the interest earned under Scheme I of company E and Scheme IV of company A respectively in two years on an amount of Rs. 1.2 lakh?
a) Rs 1428
b) Rs. 1328
c) Rs. 1528
d) Rs. 1548
e) None of these
Question 4: Company D offers compound interest under scheme II and Simple Interest under Scheme IV. Abhijt invested Rs. 25000 with this company under Scheme IV and after one year switched to Scheme II along with the interest for one more year. What is the total amount he will get at the end of two years?
a) Rs. 28939.25
b) Rs. 29838.75
c) Rs. 31748.25
d) Rs. 31738.75
e) None of these
Question 5: Abishek invested an amount of Rs. 45000 for two years with company B under scheme III, Which offers compound interest, Jeevan invested an equal amount for two years with company C under Scheme IV, which offer simple Interest. Who earned more interest and how much?
a) Abhishek, Rs. 1875
b) Jeevan, Rs. 1875
c) Abhishek, Rs. 1962
d) Jeevan, Rs. 1962
e) None of these
Question 6: Mr. Lal invested Rs. 30000 in company A under Scheme II, which offers simple interest and Rs. 48000 in Company D under Scheme II, which offers compound interest. What will be the total amount of interest earned by Mr Lal in two years?
a) Rs. 14728.80
b) Rs. 17428.50
c) Rs. 14827.70
d) Rs. 16728.20
e) None of these
Question 7: What is the difference between the simple and compound interest on Rs.7,300 at the rate of 6 p.c.p.a. in 2 years?
a) Rs.29.37
b) Rs.26.28
c) Rs.31.41
d) Rs.23.22
e) Rs.21.34
Question 8: A sum of Rs16800 is divided into two parts. One part is lent at the simple interest of 6% per annum and the other at 8% per annum. After 2 years total sum received is Rs19000. The sum lent at 6% of simple interest is
a) Rs12200
b) Rs12000
c) Rs11000
d) Rs10000
e) None of these
Question 9: Find SI if P = Rs. 1000, R = 20% per annum and duration is 4 years
a) Rs. 400
b) Rs. 600
c) Rs. 800
d) Rs. 850
e) None of these
Question 10: The effective annual rate of interest corresponding to a nominal rate of 6% per annum payable half-yearly is:
a) 6.10%
b) 6.11%
c) 6.08%
d) 6.09%
e) None of these
200 IBPS Mocks for just Rs.299
Answers & Solutions:
1) Answer (B)
Compound Interest after 2 years = 1414.4
$P(1+\frac{8}{100})^2 – P$ = 1414.4
=> $P(1.08)^2 – P$ = 1414.4
=> 0.1664P = 1414.4
=> P = 8500
Therefore amount = 8500 + 1414.14 = 9914.14
2) Answer (C)
Let principal amount be Rs. x.
(x×9×2)/100 + (x×9.5×2)/100 = 14800
or (0.18+0.19) = 14800
X = 14800/0.37 = Rs. 40000
3) Answer (A)
Scheme I of company E
CI = 120000 [(1+ 9/100)^2- 1]
= 120000 [((109×109)/(100×100)-1)]
= 120000 × 1881/10000 = Rs. 22572
Scheme IV of company A
SI = (120000×2×10)/100 = Rs. 24000
Difference = 24000 – 22572 = Rs. 1428
4) Answer (B)
25000 × 109.5/100 = 27375
And again, 27375 × 109/100 = Rs. 29838. 75
5) Answer (D)
Interest earned by Abhishek = 45000 × (1+ 8/100)^2- 45000
= 45000 × 27/25 × 27/25 = 45000
= 52488 – 45000 = 7488
Interest earned by Jeevan = (45000×10.5×2)/100 = 9450
Required difference = 9450 – 7488 = 1962
Hence, Jeevan earned Rs. 1962 more.
6) Answer (B)
(30000×9.5×2)/100 + (48000× 109/100× 109/100- 48000) = 5700 + (57028.8 – 48000)
= 5700 + 9028.8 = Rs. 14728.80
7) Answer (A)
SI = $\frac{7300 6 2}{100}$ = 876
CI = 7300[1 + $\frac{6}{100}$]2 – 7300 = 902.28
Difference = Rs26.28
8) Answer (A)
Let x be the amount lent for 6%
16800 – x is the amount lent for 8%
$\frac{2×6}{100}$ + $\frac{2(16800-x)8}{100}$ + 16800 = 19000
x = 12200
9) Answer (C)
S.I = PRT/100 = (1000×20×4)/100= Rs. 800
10) Answer (D)
Amount of Rs.100 for 1 year when compounded half-yearly = Rs.$[100\times(1+3/100)^2 ]$=Rs.106.09
Effective rate =(106.09-100) %=6.09.
To know more about the exam, try reading our other blogs on how to prepare for IBPS PO cloze test, 8 tips to improve English for IBPS PO and how to prepare for high-level data interpretation for IBPS PO.





