Geometry Questions for SSC CPO PDF
Download Top-15 SSC CPO Geometry Questions and Answers PDF, based on asked questions in previous CPO & other SSC exam papers.
Download Geometry Questions for SSC CPO PDF
Download SSC General Knowledge PDF
Question 1: What is the total number of circles passing through the two fixed points?
a) 1
b) 2
c) 4
d) Infinite
Question 2: Find the volume $(in cm^3)$ of a cube of side 4.5 cm.
a) 55.467
b) 14.445
c) 91.125
d) 26.465
Question 3: If the sum of the interior angles of a regular polygon is $720^\circ$ then how many sides does it have?
a) 8
b) 9
c) 6
d) 10
SSC CPO Free Mock Test (Latest Pattern)
SSC CPO Previous Papers (Download PDF)
Free 18000 Solved Questions: SSC Study Material
Question 4: The length of one side and the diagonal of a rectangle are 20 cm and 29 cm respectively. Find the length of its other side (in cm).
a) 42
b) 30
c) 21
d) 60
Question 5: AB is the chord of circle of length 6 cm. From the center of the circle a perpendicular is drawn which intersects the chord at M and distance between centre and chord is 4 cm. find the area $(in cm^2)$ of the circle)
a) 55
b) 61.5
c) 70
d) 78.5
Question 6: The two chords AB and CD of a circle intersect at point P, such that BP=4 cm, PD=5 cm, and CP=8 cm. find the length of chord AB.
a) 8
b) 10
c) 12
d) 14
Question 7: Find the total surface area $(in cm^2)$ of a right circular cylinder of diameter 28 cm and height 12 cm.
a) 2200
b) 2080
c) 1920
d) 2288
Question 8: The circumference of a circle is 110 cm. Find its radius (in cm).
a) 35
b) 19.5
c) 17.5
d) 39
Question 9: The area of a square is $30.25 cm^2$. Find its perimeter (in cm).
a) 44
b) 23
c) 22
d) 46
SSC CPO Previous Question Papers (download pdf)
Question 10: The base and height of a right angled triangle is 12 cm and 5 cm respectively. Find the circum-radius (in cm) of the triangle.
a) 5
b) 6
c) 6.5
d) 7
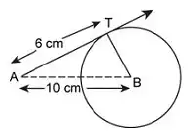
Question 11: For the circle shown below, find the length (in cm) of the largest cord of the circle.
a) 8
b) 12
c) 16
d) 18
Question 12: The volume of a cube is $274.625 cm^3$. Find its side (in cm).
a) 7.5
b) 6.5
c) 5.5
d) 3.5
Question 13: If the perimeter of a semicircle is 72 cm, then find its area $(in cm^2)$.
a) 308
b) 616
c) 160
d) 320
Question 14: The area of a square is $42.25 cm^2$. Find its perimeter (in cm).
a) 52
b) 26
c) 28
d) 56
Question 15: The area of a right angled triangle ABC, right angled at B, is 46 sq units. A median is drawn from A to BC which intersects at D. Find the area (in sq. units) of triangle ABD.
a) 12
b) 23
c) 46
d) 88
Free SSC Study Material (18,000 Solved Questions)
Download SSC CPO Previous Papers (Download PDF)
Answers & Solutions:
1) Answer (D)
Let there be 2 fixed points, as we can see from the figure that there can be infinite circles that passes through these 2 fixed points.
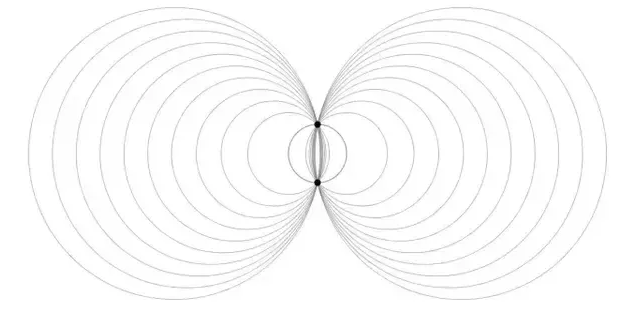
=> Ans – (D)
2) Answer (C)
Side of cube = $a=4.5$ cm
=> Volume of cube = $a^3$
= $(4.5)^3=91.125$ $cm^3$
=> Ans – (C)
3) Answer (C)
Sum of all interior angles of a polygon with $’n’$ sides = $(n-2)\times180^\circ$
Let the number of sides be $n$
=> Sum of interior angles = $(n-2)\times180^\circ=720^\circ$
= $(n-2)=\frac{720^\circ}{180^\circ}=4$
=> $n=4+2=6$
=> Ans – (C)
4) Answer (C)
Let the length of rectangle = $l$ cm and breadth, $b=20$ cm
=> Diagonal, $d^2=l^2+b^2$
=> $l^2=(29)^2-(20)^2$
=> $l^2=841-400=441$
=> $l=\sqrt{441}=21$
$\therefore$ Length of its other side = 21 cm
=> Ans – (C)
5) Answer (D)

Given : AB = 6 cm and OM = 4 cm
To find : Area of circle = ?
Solution : Let $r$ be the radius of circle
Also, MB = $\frac{6}{2}=3$ cm
In right $\triangle$ MOB,
=> $(OB)^2=(OM)^2+(MB)^2$
=> $(OB)^2=(4)^2+(3)^2$
=> $r^2=16+9=25$
=> $r=\sqrt{25}=5$ cm
$\therefore$ Area of circle = $\pi r^2$
= $3.14 \times(5)^2=78.5$ $cm^2$
=> Ans – (D)
6) Answer (D)
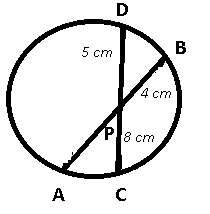
Given : AB and CD are chords of the circle which intersect at point P. BP = 4 cm, CP = 8 cm and PD = 5 cm
To find : AB = ?
Solution : Let AP = $x$ cm
Now, when two chords intersect each other inside a circle, the products of their segments are equal.
=> $(AP)\times(BP)=(CP)\times(DP)$
=> $x\times4=8\times5$
=> $x=\frac{40}{4}=10$
$\therefore$ AB = AP + PB = $10+4=14$ cm
=> Ans – (D)
7) Answer (D)
Height of cylinder, $h=12$ cm and radius, $r=\frac{28}{2}=14$ cm
Total surface area of cylinder = $2\pi r(r+h)$
= $2\times\frac{22}{7}\times14\times(14+12)$
= $88\times26=2288$ $cm^2$
=> Ans – (D)
8) Answer (C)
Let radius of circle = $r$ cm
=> Circumference = $2\pi r=110$
=> $2\times\frac{22}{7}\times r=110$
=> $r=110\times\frac{7}{44}$
=> $r=2.5\times7=17.5$ cm
=> Ans – (C)
9) Answer (C)
Let side of square = $s$ cm
=> Area = $s^2=30.25$
=> $s=\sqrt{30.25}=5.5$ cm
$\therefore$ Perimeter = $4\times5.5=22$ cm
=> Ans – (C)
10) Answer (C)
Length of base and height of triangle = 12 and 5 cm
=> Let length of hypotenuse = $x$ cm
=> $(x)^2=(12)^2+(5)^2$
=> $(x)^2=144+25=169$
=> $x=\sqrt{169}=13$ cm
Also, the circumcentre of a right angled triangle lies on its hypotenuse, thus circumradius = $\frac{1}{2}\times$ (hypotenuse)
= $\frac{1}{2}\times13=6.5$ cm
=> Ans – (C)
11) Answer (C)

Given : AT is tangent on the circle. AT = 6 cm and AB = 10 cm
To find : Largest chord = Diameter = ?
Solution : In right $\triangle$ ABT
=> $(BT)^2=(AB)^2-(AT)^2$
=> $(BT)^2=(10)^2-(6)^2$
=> $(BT)^2=100-36=64$
=> $BT=\sqrt{64}=8$ cm
$\therefore$ Diameter = $2\times8=16$ cm
=> Ans – (C)
12) Answer (B)
Let side of cube = $a$ cm
Volume of cube = $a^3=274.625$
=> $a=\sqrt[3]{6.5\times42.25}$
=> $a=6.5$ cm
=> Ans – (B)
13) Answer (A)
Let radius of semi circle = $r$ cm
=> Perimeter of semi circle = $\pi r+2r=72$
=> $r(\frac{22}{7}+2)=72$
=> $r(\frac{22+14}{7})=72$
=> $r=72\times\frac{7}{36}=14$ cm
$\therefore$ Area of semi-circle = $\frac{1}{2} \pi r^2$
= $\frac{1}{2}\times\frac{22}{7}\times(14)^2$
= $22\times14=308$ $cm^2$
=> Ans – (A)
14) Answer (B)
Let side of square = $s$ cm
=> Area = $s^2=42.25$
=> $s=\sqrt{42.25}=6.5$ cm
$\therefore$ Perimeter of square = $4s=4\times6.5=26$ cm
=> Ans – (B)
15) Answer (B)
Note :- A median divides a triangle into two parts of equal areas.
Proof :
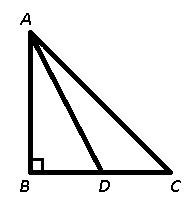
It is given that $ar(\triangle ABC)=46$ sq.units
Also, AD bisects BC, let BC = $2x$ units => BD = $\frac{2x}{2}=x$ units
$\therefore$ $\frac{ar(\triangle ABD)}{ar(\triangle ABC)}=\frac{\frac{1}{2}\times(AB)\times(BD)}{\frac{1}{2}\times(AB)\times(BC)}$
=> $\frac{\triangle}{46}=\frac{x}{2x}$
=> $\triangle=\frac{46}{2}=23$ sq.units
=> Ans – (B)
We hope this Geometry Questions PDF for SSC CPO Exam will be highly useful for your preparation.





