Geometry Questions For SSC CHSL PDF
SSC Stenographer Constable Geometry Question and Answers download PDF based on previous year question paper of SSC Stenographer exam. 10 Very important Geometry questions for Stenographer Constable.
GEOMETRY Questions FOR SSC CHSL PDF
285 SSC MOCKS FOR JUST RS. 249
Download Topic Wise SSC CHSL Important Questions PDF
SSC CHSL Study Material (FREE Tests)
Question 1: Point R lies on line segment PQ such that PR = 24 cm and RQ = 6 cm. Points S and T lie on the same side of line PQ such that $\triangle$PRS and $\triangle$RQT are equilateral triangles. If M and N are mid points of line segment PT and QS respectively, then find out the area of $\triangle$MNR.
a) $\dfrac{117\sqrt{3}}{4}$ sq. cm
b) $\dfrac{63\sqrt{3}}{\sqrt{2}}$ sq. cm
c) $\dfrac{121\sqrt{5}}{\sqrt{5}}$ sq. cm
d) $\dfrac{103\sqrt{3}}{4}$ sq. cm
Question 2: It is given that AO = BO and PA and PC are tangent to the circle. If $\angle$OBC = $x$° then find out the value of $20x$?

Question 3: A circle contains 2 perpendicular chords AB and CD. The length of chord AB is 6 cm and that of chord CD is 12 cm. C is closer to A and B than D. If it is known that chord CD passes through O, the centre of the circle, what is the area of the polygon AOBD?
a) 9 $ cm^2$
b) 18 $cm^2$
c) 36 $cm^2$
d) 27 $cm^2$
Question 4: 3 circles of equal size are tightly packed inside a larger circle such that the 3 circles touch each other externally and touch the larger circle internally. If the diameter of the smaller circle is ‘r’, then the area outside the smaller circles but inside the larger circle is
a) $\pi r^2(\frac{2\sqrt{3}-5}{3})$
b) $\frac{\pi r^2}{4}(\frac{4\sqrt{3}-2}{3} )$
c) $\frac{\pi r^2}{4}(\frac{2\sqrt{3}-4}{3})$
d) $\frac{\pi r^2}{4}(\frac{2\sqrt{3}+13}{3})$
Question 5: What is the volume of a regular tetrahedron whose side measures 20 cm?
a) $471.4 cm^3$
b) $1414.2 cm^3$
c) $942.8 cm^3$
d) $1885.6 cm^3$
Question 6: In a triangle ABC, P, Q, R are points on the sides AB, BC, AC respectively such that RQ = CQ and PQ = BQ. Find $\angle{PQR}$ when $\angle{CAB} = 60$° ?(In degrees)
Question 7: In the figure given below, if ‘C’ is the centre of the circle and a,b,c are the areas of the Triangle PQR, Square QTRC and Circle respectively. Find the ratio a:b:c.
a) $\sqrt{3}$:$1$:$\pi$
b) $\pi$:$1$:$\pi$
c) $1$:$\sqrt{3}$:$\pi$
d) $1$:$1$:$\pi$
FREE SSC MATERIAL – 18000 FREE QUESTIONS
Question 8: Find the area bounded by the graph y = |x+p| and y = 6
a) 72
b) 54
c) 36
d) Data Insufficient
Question 9: An equilateral triangle GCD is constructed on side CD of a square ABCD. E is midpoint of side AB. What is the ratio of Area inside square ABCD and outside triangle EDC to the area of polygon DECG?
a) $ \frac{ 2\sqrt{3} }{2 – \sqrt{3}} $
b) $ \frac{\sqrt{3}}{2 – \sqrt{3}} $
c) $ \frac{ 2 }{ 2 – \sqrt{3} } $
d) $ \frac{ 2 }{ 2\sqrt{3} -2 } $
e) $ \frac{ 2\sqrt{3} -2 }{2} $
Question 10: A square EFGH of side 6 cm is drawn in an equilateral triangle ABC such that GH lie along BC. E is on side AB and F is on side AC respectively. Find the side of the triangle?
a) (3 + 6√3) cm
b) (4√3 + 6) cm
c) (4 + 6√3) cm
d) (4 + 3√3) cm
e) (6 + 3√3) cm
DOWNLOAD APP TO ACESSES DIRECTLY ON MOBILE
Answers & Solutions:
1) Answer (A)
Let us solve this problem with the help of co-ordinate geometry. Assume that point P is at origin and Q is at (30, 0) then co-ordinates of R = (24, 0).

We are given that points S and T lie on the same side of line PQ such that $\triangle$PRS and $\triangle$RQT are equilateral triangles. Hence we can say that PR = RS = PS = 24 units and RQ = QT = RT = 6 units.
We know that height of an equilateral trianlge = $\dfrac{\sqrt{3}a}{2}$
In triangle PSR,
‘x’ co-ordinate of point S will be half of the sum of the ‘x’ co-ordinates of vertices P and R.
‘y’ co-ordinate of point S will be equal to height of the triangle PSR.
Hence co-ordinates of vertex S = ($\dfrac{0+24}{2}$, $\dfrac{24\sqrt{3}}{2}$) = ($12$, $12\sqrt{3}$)
Similarly in triangle RTQ,
Co-ordinates of vertex T = ($\dfrac{24 + 30}{2}$, $\dfrac{6\sqrt{3}}{2}$) = ($27$, $3\sqrt{3}$).
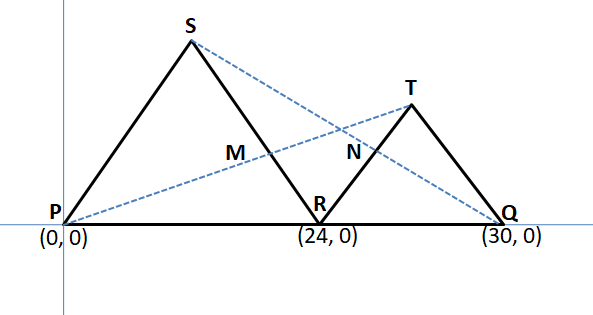
It is given that M and N are mid points of line segment PT and QS respectively, hence,
Co-ordinates of the point M = ($\dfrac{0 + 27}{2}$, $\dfrac{0 + 3\sqrt{3}}{2}$) = ($\dfrac{27}{2}$, $\dfrac{3\sqrt{3}}{2}$).
Co-ordinates of the point N = ($\dfrac{30 + 12}{2}$, $\dfrac{0 + 12\sqrt{3}}{2}$) = ($21$, $6\sqrt{3}$).
Also co-ordinates of the pointR = (24, 0).
Now that we have all thee vertices of triangle MNR we can find the distance MN, NR and MR.
MN = $\sqrt{(21-\dfrac{27}{2})^2 + (6\sqrt{3}-\dfrac{3\sqrt{3}}{2})^2}$ = $\sqrt{(\dfrac{15}{2})^2 + (\dfrac{9\sqrt{3}}{2})^2}$ = $3\sqrt{13}$
NR = $\sqrt{(24-21)^2 + (0-6\sqrt{3})^2}$ = $3\sqrt{13}$
MR = $\sqrt{(24-\dfrac{27}{2})^2 + (0-\dfrac{3\sqrt{3}}{2})^2}$ = $\sqrt{(\dfrac{21}{2})^2 + (\dfrac{3\sqrt{3}}{2})^2}$ = $3\sqrt{13}$
We can see that MN = NR = MR. Hence we can say that triangle MNR is an equilateral triangle.
Therefore, the area of triangle MNR = $\dfrac{\sqrt{3}}{4}\times (3\sqrt{13})^2$ = $\dfrac{117\sqrt{3}}{4}$ sq. cm
Hence, option A is the correct answer.
2) Answer: 1275
Drawing AQ and QB where Q is the centre of the circle. In quadilateral PAQB
$\angle$PAQ+$\angle$AQB+$\angle$QBP+$\angle$BPA = 360°
We know that angle subtend by tangent of centre of circle = 90° i.e. $\angle$PAQ = $\angle$QBP = $\angle$QBC = 90°
$\Rightarrow$ 90°+$\angle$AQB+90°+75° = 360°
$\Rightarrow$ $\angle$AQB = 105°
We know that angle subtend by a chord on centre is twice of the angle subtend on perimeter. therefore
$\angle$AOB=$\frac{1}{2}\angle$ AQB
$\Rightarrow$ $\angle$AOB = $\frac{1}{2}\times 105$ = 52.5°

Since AO = OB therefore $\angle$AOQ = $\angle$BOQ = $\frac{1}{2}\times$ $\angle$AOB
$\Rightarrow$ $\angle$AOQ=$\angle$BOQ=$\frac{1}{2}\times$ 52.5° = 26.25°
In $\triangle$ QBO,
$\Rightarrow$ QB = QO therefore
$\angle$QBO = $\angle$QOB = 26.25°
We know that $\angle$QBC = $\angle$QBO + $\angle$OBC = 90°
$\Rightarrow$ $\angle$OBC = 90° – 26.25° = 63.75°= $x$°
The value of 20$x$ = 20*63.75 = 1275. Hence 1275 is the correct answer.
FREE MOCK TEST FOR SSC STENOGRAPHER
3) Answer (B)
CD passes through the centre of the circle. Therefore, CD must be the diameter of the circle.
Length of CD = 12 cm
=> Radius of the circle = 6 cm.
Length of AB = 6 cm.

If we connect AB to the centre of the circle, we will get an equilateral triangle (All 3 sides will be 6 cm).
Now, let us join A and D and B and D.
$\angle AOB$ = 60ᵒ (Since triangle AOB is an equilateral triangle).
$\angle AOB$ and $\angle ADB$ are subtended by the same chord, $AB$.
Therefore, $\angle ADB$ = 30ᵒ (Angle subtended by a chord on the circumference is half of the angle subtended by the same chord on the centre).
Now, in triangle AOB, AO = BO= 6 cm (Radii of the circle).
$\angle ADO$ = 30ᵒ/2 = 15ᵒ (Since the figure is symmetrical about CD).
=> $\angle OAD$ = 15ᵒ (Since triangle AOD is isosceles).
Therefore, $\angle AOD$ = 180ᵒ – 15ᵒ – 15ᵒ = 150ᵒ.
Area of triangle AOD = 0.5*r*r*sin 150ᵒ
= 0.5*6*6*0.5
= 9 $cm^2$
Area of the figure AOBD = 2* Area of triangle AOD
= 2*9
= 18 $cm^2$
Therefore, option B is the right answer.
4) Answer (B)
The radius of the smaller circle is $\frac{r}{2}$ since it has been given that the diameter is $r$.

On joining the radii of the 3 circles, we get an equilateral triangle with side $r$.
The incentre of this equilateral triangle will also be the centre of the larger circle.
Inradius of the equilateral triangle = $\frac{r}{2\sqrt{3}}$
Radius of the outer circle = Radius of the smaller circle + Circumradius of the triangle.
=> Radius of the outer circle = $\frac{r}{2} + \frac{r}{\sqrt{3}}$
Area of the larger circle = $\pi * [\frac{r}{2}*(1 + \frac{2}{\sqrt{3}})]^2$
= $\frac{\pi*r^2}{4}* (1+\frac{4}{3} + \frac{4}{\sqrt{3}})$
=$\frac{\pi*r^2}{4}*(\frac{7+4\sqrt{3}}{3})$
Area of the smaller circles = $3*\frac{\pi r^2}{4}$, since $r$ is the diameter here.
Difference between the areas = $\frac{\pi r^2}{4}(\frac{7+4\sqrt{3}}{3} – 3)$
= $\frac{\pi r^2}{4}(\frac{4\sqrt{3}-2}{3})$
Therefore, option B is the right answer.
5) Answer (C)
It has been provided that the tetrahedron is regular.
In solid geometry, the volume of a pyramid is one-third the volume of a prism with similar height.
Tetrahedron is a special case of a pyramid.
Let us first find out the volume of the prism and then divide it by 3.
All the 4 triangular faces in a tetrahedron are congruent. Therefore, the height of the triangle will be the slant height of the tetrahedron.
Let us assume the side of the triangle to be $a$.
Inradius = $a/2\sqrt{3}$
Inradius, Height of the tetrahedron and height of the triangle form a right angled triangle.

Applying Pythagoras theorem, we get, $h^2+(a/2\sqrt{3})^2 = (\sqrt{3}a/2)^2$
Height of the tetrahedron = $\frac{\sqrt{6}a}{3}$
Volume of tetrahedron, V = (1/3)* area of the base triangle* height of the tetrahedron
= $\frac{1}{3}* \frac{\sqrt{3}a^2}{4}*\frac{\sqrt{6}a}{3}$
= $ \frac{a^3}{6\sqrt{2}}$
Now, we can find the volume of the tetrahedron by substituting the value of $a = 20$.
$ V = \frac{20^3}{6\sqrt{2}}$
$ V = \frac{8000}{6\sqrt{2}}$
$V = 942.8 cm^3$
Hence, option C is the right answer.
Alternate solution:
The volume of a tetrahedron is given by the formula, $V = \frac{a^3}{6\sqrt{2}}$.
By substituting $a=20$, we can find the answer.
FREE SSC PRACTICE SET (DAILY TEST)
6) Answer: 60
Let us take $\angle {C} = c$ and $\angle {B} = b$
From the figure below
60+b+c = 180
b+c = 120
In triangle QRC
2c+e = 180………..(I)
In triangle PQB
2b+f = 180………..(II)
(I)+(II)
2(b+c)+e+f = 360
e+f = 120
$\angle{PQR} = 180-(e+f) = 60$
7) Answer (D)
let the radius of the circle be ‘r’
The length of the side of the square is equal to ‘r’
Area of the square QTRC, b = $r^{2}$
Area of triangle PQR, a = $\frac{1}{2}$*$2r$*$r$ = $r^{2}$ (height of the triangle is equal to that of the radius $r$ of the circle.)
Area of Circle, c =$\pi$*$r^{2} $
a:b:c = $1$:$1$:$\pi$
8) Answer (C)

Look at the figure.
Since slope of the lines is 1
Anfle CBO = Angle DCB = 45
BD = DC = 6
Similarly AD = 6
Area = 1/2 *12*6 = 36
9) Answer (C)
Let side of square be ‘$a$’
Area of triangle EDC => $ \frac{1}{2} \times a \times a $ = $ \frac{a^2}{2} $
Area of triangle GDC => $ \frac{\sqrt{3}a^2}{4} $
Area of polygon DECG => $ \frac{a^2}{2} – \frac{\sqrt{3}a^2}{4} $ = $ \frac{ (2 -\sqrt{3})a^2 }{4} $
Area inside square ABCD and outside triangle EDC => $ \frac{a^2}{2} $
Ratio => $ \frac{\frac{a^2}{2}}{ \frac{ (2 -\sqrt{3})a^2 }{4} } $ = $ \frac{ 2 }{ 2 – \sqrt{3} } $
Hence, option C is correct.
10) Answer (B)
Drawing a perpendicular from vertex A to the side EF to intersect it at point D
ED/DA = tan30°
By Symmetry, ED = 3 cm
=> DA = 3√3 cm
Altitude of the triangle => (6 + 3√3) cm
Side of the triangle => ( 2/√3 ) (6 + 3√3) cm
Side of the triangle => (4√3 + 6) cm
Hence, option B is correct.
FREE SSC CHSL MOCK TEST SERIES
We hope this Geometry questions for SSC Stenographer will be highly useful for your preparation.












