Geometry Questions for IIFT PDF
Download important IIFT Geometry Questions PDF based on previously asked questions in IIFT and other MBA exams. Practice Geometry questions and answers for IIFT exam.
Download Geometry Questions for IIFT PDF
Get 50% Off on IIFT & Other MBA Test Series
Download IIFT Previous Papers PDF
Practice IIFT Mock Tests
Question 1: In a square PQRS, A and B are two points on PS and SR such that PA =2AS, and RB = 2BS If PQ = 6, the area of the triangle ABQ is (in sq. cm)
a) 6
b) 8
c) 10
d) 12
e) 14
Question 2: ABCD is a quadrilateral inscribed in a circle with centre O. If $\angle COD = 120$ degrees and $\angle BAC = 30$ degrees, then the value of $\angle BCD$ (in degrees) is
Question 3: Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is
a) $9\pi-18$
b) 18
c) $9\pi$
d) 9
Question 4: A chord AB of length 24 cm is drawn in a circle of radius 13cm.Find the area of the shaded portion APB.
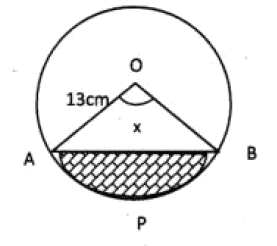
a) $13\pi xm^{2}$
b) $\frac{13\pi x}{180}cm^{2}$
c) $\frac{169\pi x}{360}-60cm^{2}$
d) $\frac{169\pi x}{180}-60cm^{2}$
Question 5: A rectangular plank $\sqrt{10}$ metre wide, is placed symmetrically along the diagonal of a square of side 10 metres as shown in the figure. The area of the plank is:
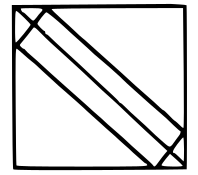
a) $10(\sqrt{20}-1)$ sq.mt
b) $10(\sqrt{5}-1)$ sq.mt
c) $10\sqrt{20}-1$ sq.mt
d) None
Question 6: If in the figure below, angle XYZ = 90° and the length of the arc XZ = 10π, then the area of the sector XYZ is
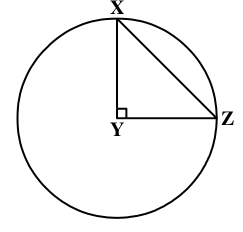
a) 10π
b) 25π
c) 100π
d) None of the above
Question 7: A ladder just reaches a window that is 8 metres high above the ground on one side of the street. Keeping one end of the ladder at the same place, the ladder is moved to the other side of the street so as to reach a 12 metre high window. If the ladder is 13 metres long, what is the width of the street?
a) 14.6 metres.
b) 15.8 metres.
c) 15.2 metres.
d) 15.5 metres.
Question 8: A parallelogram ABCD has area 48 sqcm. If the length of CD is 8 cm and that of AD is s cm, then which one of the following is necessarily true?
a) $s≠6$
b) $s \geq 6$
c) $5 \leq s \leq 7$
d) $s \leq 6$
Question 9: On a triangle ABC, a circle with diameter BC is drawn, intersecting AB and AC at points P and Q, respectively. If the lengths of AB, AC, and CP are 30 cm, 25 cm, and 20 cm respectively, then the length of BQ, in cm, is
Question 10: ABCD is a quadrilateral inscribed in a circle with centre O. If $\angle COD = 120$ degrees and $\angle BAC = 30$ degrees, then the value of $\angle BCD$ (in degrees) is
Answers & Solutions:
1) Answer (C)
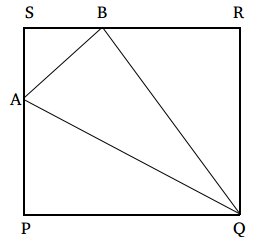
PQ = QR = RS = SP = 6 cm
PA = 2AS and PA + AS = 6cm
=> PA = 4 cm and AS = 2 cm
Similarly, RB = 2BS and RB + BS = 6 cm
=> RB = 4 cm and BS = 2cm
Area of △ ABQ = area of PQRS – area of △APQ – area of △RBQ – area of △ASB
= (36 – 12 – 12 – 2) sq. cm
= 10 sq. cm
Hence, option C is the correct answer.
Top 500+ Free Questions for IIFT
IIFT Previous year question answer PDF
2) Answer: 90
$\angle COD = 120$ => $\angle CAD = 120/2 = 60$
$\angle BAC = 30$
$\angle BAD = \angle BAC + \angle CAD$ = 30 + 60 = 90.
$\angle BCD = 180 – \angle BAD$ = 180 – 90 = 90
3) Answer (B)
The image of the figure is as shown.
AB = AC = 6cm. Thus, BC = $\sqrt{6^2 + 6^2}$ = 6√2 cm
The required area = Area of semi-circle BQC – Area of quadrant BPC + Area of triangle ABC
Area of semicircle BQC
Diameter BC = 6√2cm
Radius = 6√2/2 = 3√2 cm
Area = $\pi r^2 $/2 = $ \pi$ * $(3 \sqrt{2})^2 $/2 = 9$\pi$
Area of quadrant BPC
Area = $\pi r^2$/4 = $\pi*(6)^2$/4 = 9$\pi$
Area of triangle ABC
Area = 1/2 * 6 * 6 = 18
The required area = Area of semi-circle BQC – Area of quadrant BPC + Area of triangle ABC
= 9$\pi$ – 9$\pi$ + 18 = 18
4) Answer (C)
In $\triangle$OAB
OC is drawn perpendicular to AB
By symmetry AC=CB=AB/2 =24/2= 12
OA=13
$OC^{2}=OA^{2}-AC^{2}$
$OC^{2}=13^{2}-12^{2}$=25
OC=5
So area of shaded region = Area of sector OAPB – Area of $\triangle$OAB
=$\frac{x}{360}*\pi*(OA)^{2}$-$\frac{1}{2}*(AB)*(OC)$
=$\frac{x}{360}*\pi*(13)^{2}$-$\frac{1}{2}*(24)*(5)$
=$\frac{169\pi x}{360}-60cm^{2}$
5) Answer (A)
In the given diagram AB=$\sqrt{10}$ m
Given that PQRS is a square and the plank is placed symmetrically $\triangle$BPA and $\triangle$AQC will be isosceles right triangles.
So PA=PB=$\frac{\sqrt{10}}{\sqrt{2}}$=$\sqrt{5}$ m
PQ= PA+AQ
AQ= PQ-PA=10-$\sqrt{5}$ m
We know that AQ=QC ($\triangle$AQC is isosceles right triangle)
So AC=$\sqrt{2}$AQ=$\sqrt{2}$*(10-$\sqrt{5}$) m
Now we can calculate area of plank
Area of ABCD= AB*AC= $\sqrt{10}$*$\sqrt{2}$(10-$\sqrt{5}$)=10($\sqrt{20}$-1) sq. mt
6) Answer (C)
Length of arc XZ is the perimeter of quarter circle.
$\frac{\pi r}{2}$ = 10$\pi$
r=20
Area of sector XYZ = Area of quarter circle = $\frac{\pi r^{2}}{4}$
Area = 100$\pi$
7) Answer (C)
We can represent the given information in the diagram as follows:
The width of the street = BD = BC + CD
$\Rightarrow$ $\sqrt{13^2 – 8^2}$ + $\sqrt{13^2 – 12^2}$
$\Rightarrow$ $10.24$m + $5$m = 15.2 m. Hence, option C is the correct answer.
8) Answer (B)
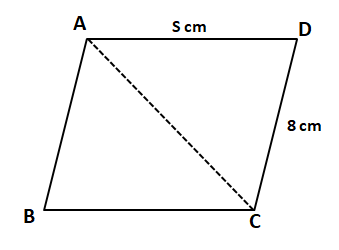
We can see that area of parallelogram ABCD = 2*Area of triangle ACD
48 = 2*Area of triangle ACD
Area of triangle ACD = 24
$(1/2)*CD*DA*sinADC=24$
$AD*sinADC=6$
We know that $sin\theta$ $\leq$ 1, Hence, we can say that AD $\geq$ 6
$\Rightarrow$ s $\geq$ 6
9) Answer: 24
Let us draw the diagram according to the available information.
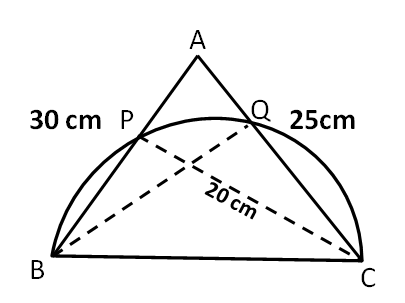
We can see that triangle BPC and BQC are inscribed inside a semicircle. Hence, we can say that
$\angle$ BPC = $\angle$ BQC = 90°
Therefore, we can say that BQ $\perp$ AC and CP $\perp$ AB.
In triangle ABC,
Area of triangle = (1/2)*Base*Height = (1/2)*AB*CP = (1/2)*AC*BQ
$\Rightarrow$ BQ = $\dfrac{AB*CP}{AC}$ = $\dfrac{30*20}{25}$ = 24 cm.
10) Answer: 90
$\angle COD = 120$ => $\angle CAD = 120/2 = 60$
$\angle BAC = 30$
$\angle BAD = \angle BAC + \angle CAD$ = 30 + 60 = 90.
$\angle BCD = 180 – \angle BAD$ = 180 – 90 = 90
IIFT Previous year question answer PDF
We hope this Geometry questions and answers PDF will be helpful to you.
