Expected Maths Questions for SSC CGL 2020 PDF
Download SSC CGL Questions on Expected Maths PDF based on previous papers very useful for SSC CGL Exams. Top-10 Very Important Maths Questions for SSC CGL Exam.
Download Expected Maths Questions for SSC CGL 2020 PDF
Get 200 SSC mocks for just Rs. 249. Enroll here
Question 1: ABCD is a square. Draw an equilateral triangle PBC on side BC considering BC is a base and an equilateral triangle QAC on digonal AC considering AC is a base. Find the value of $\ \frac{Area \ of \ \triangle PBC}{Area \ of \ \triangle QAC}$
a) $\frac{1}{2}$
b) 1
c) $\frac{1}{3}$
d) $\frac{1}{4}$
Question 2: A ladder is placed along a wall such that its upper end is touching the top of the wall. The foot of the ladder is 10 ft away from the wall and the ladder is making an angle of $60^{0}$ with the ground. When a man starts climbing on it, it slips and now ladder makes an angle of 30° with ground. How much did the ladder slip from the top of the wall?
a) 12 ft
b) 20 ft
c) 7.32 ft
d) 18 ft
Question 3: A man rows to a place 35 km in distant and back in 10 hours 30 minutes. He found that he could row 5 km with the flow of stream in the same time as he can row 4 km against the stream. Find the rate of flow of the stream.
a) 1 km/hr
b) 0.5 km/hr
c) 0.75 km/hr
d) 1.5 km/hr
Question 4: A vegetable seller sells his vegetables at 20% profit. At the same time he uses false weights, which is 10% less than the actual weight. What will be his total gain percentage ?
a) 25%
b) 30%
c) 33.33%
d) 18 $\ \frac{7}{9}$%
Take a free mock test for SSC CGL
Download SSC CGL Previous Papers PDF
18000+ Questions – Free SSC Study Material
Question 5: If $(5\sqrt5 x^3 – 81 \sqrt3 y^3) \div (\sqrt5 x – 3\sqrt3 y) = (Ax^2 + By^2 +Cxy)$,then the value of $(6A + B – \sqrt{15} C)$ is:
a) 10
b) 9
c) 15
d) 12
Question 6: A root of equation $ax^2 + bx + c = 0$ (where $a, b$ and $c$ are rational numbers) is $5 + 3\surd3$. What is the value of $\frac{(a^2 + b^2 + c^2)}{(a + b + c)}$?
a) $\frac{35a}{3}$
b) $\frac{37a}{3}$
c) $\frac{-105a}{11}$
d) $\frac{-105a}{13}$
Question 7: Rs 60500 is divided among A, B and C such that A receives 2/9 as much as B and C together and B receives 3/7 of as much as A and C together. What is the share of C (in Rs)?
a) 29850
b) 30120
c) 31350
d) 37250
More SSC CGL Important Questions and Answers PDF
Question 8: A wire, when bent in the form of a square, encloses a region of area 121 $cm^{2}$ .If the same wire is bent in to the form of a circle, then the area of the circle is use ($\pi$=$\frac{22}{7}$)
a) 150 $cm^{2}$
b) 152 $cm^{2}$
c) 154 $cm^{2}$
d) 159 $cm^{2}$
Question 9: Consider the two equiangular triangles ABC and DEF having medians as AL and DM respectively as shown in figure below.
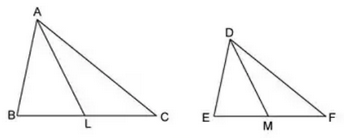Choose the correct option for the above situation.a) $\frac{BC}{EF}=\frac{DM}{AL}$
b) $\frac{BC}{EF}=\frac{AL}{DM}$
c) $\frac{EF}{BC}=\frac{AL}{DM}$
d) All options are Correct
Question 10: If a shopkeeper marks the price of goods 40% more than their cost price and allows a discount of 40%, then what is his gain or loss percent?
a) 16%, Loss
b) 16%, Profit
c) 10%, Loss
d) 12%, Profit
SSC CGL Previous Papers Download PDF
Answers & Solutions:
1) Answer (A)
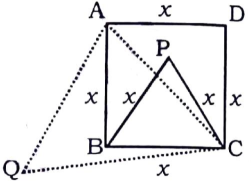
Let side of the square be $x$ cm
=> Side of equilateral $\triangle$ PBC = $x$ cm
In right $\triangle$ ABC,
=> $(AC)^2=(AB)^2+(BC)^2$
=> $(AC)^2=(x)^2+(x)^2=2x^2$
=> $AC=\sqrt2x$
$\therefore$ $\ \frac{ar(\triangle PBC)}{ar(\triangle QAC)}$
= $[\frac{\sqrt3}{4}\times (x)^2]\div[\frac{\sqrt3}{4}\times (\sqrt2x)^2]$
= $\frac{x^2}{2x^2}=\frac{1}{2}$
=> Ans – (A)
2) Answer (C)
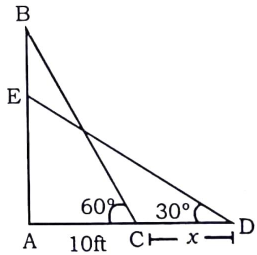
Given : BC is the initial position of the ladder, and DE is its final position. So, DE = BC (as both are the same ladders)
To find : CD = $x=?$
Solution : In $\triangle$ ABC,
=> $cos(60^\circ)=\frac{AC}{BC}$
=> $\frac{1}{2}=\frac{10}{BC}$
=> $BC=10\times2=20$
Thus, $DE=BC=20$
Similarly, in $\triangle$ ADE,
=> $cos(30^\circ)=\frac{AD}{DE}$
=> $\frac{\sqrt3}{2}=\frac{x+10}{20}$
=> $x+10=10\sqrt3$
=> $x=10(\sqrt3-1)$
=> $x=10\times0.732=7.32$
$\therefore$ The ladder slipped 7.32 ft
=> Ans – (C)
3) Answer (C)
Let speed of man in still water = $x$ km/hr and speed of stream = $y$ km/hr
Speed downstream = $(x+y)$ km/hr and speed upstream = $(x-y)$ km/hr
The man can row 35 km to and back in 10 hours 30 minutes.
Using, time = distance/speed
=> $\frac{35}{x+y}+\frac{35}{x-y}=10.5$
=> $\frac{1}{x+y}+\frac{1}{x-y}=\frac{10.5}{35}$
=> $\frac{1}{x+y}+\frac{1}{x-y}=0.3$ ————-(i)
Also, $\frac{5}{x+y}=\frac{4}{x-y}$
=> $5x-5y=4x+4y$
=> $5x-4x=4y+5y$
=> $x=9y$ ————-(ii)
Substituting above value in equation (i), we get :
=> $\frac{1}{9y+y}+\frac{1}{9y-y}=0.3$
=> $\frac{1}{10y}+\frac{1}{8y}=0.3$
=> $\frac{10+8}{80}=0.3y$
=> $0.3y\times80=18$
=> $y=\frac{18}{24}=0.75$
$\therefore$ Rate of flow of the stream = 0.75 km/hr
=> Ans – (C)
4) Answer (C)
Let cost price of vegetables = Re 1/gm = Rs. 1000/kg
Selling price = after 20% profit = $1000+(\frac{20}{100}\times1000)=Rs.$ $1200$
Similarly, weight used while selling = $1000-(\frac{10}{100}\times1000)=900$ gm
=> Selling price = Rs. $\frac{1200}{900}=1.33$ per gm
$\therefore$ Profit % = $\frac{(1.33-1)}{1}\times100=33.33\%$
=> Ans – (C)
5) Answer (D)
$(5\sqrt5 x^3 – 81 \sqrt3 y^3) \div (\sqrt5 x – 3\sqrt3 y)$
Using the formula ,
$ (a^3 – b^3) = (a -b)(a^2 +ab +b^2)$
$(5\sqrt5 x^3 – 81 \sqrt3 y^3) \div (\sqrt5 x – 3\sqrt3 y) $
= $5x^2 + 3\sqrt15xy + 9\sqrt{3}y^2$
A = 5 , B = 27 , C=3$\sqrt15$
Putting these values in ,
$(6A + B – \sqrt{15} C)$ = 30 + 27 – 45 =12
So , the answer would be Option d)12.
6) Answer (C)
$ax^2 + bx + c = 0$ has $5 + 3\surd3$ and so the other root is $5 – 3\surd3$ since these roots occur in pairs
sum of the roots= $5 + 3\surd3$+$5 – 3\surd3$
=10
Product of the roots=($5 + 3\surd3$)($5 – 3\surd3$)
=-2
Sum of the roots=-b/a
Product of the roots=c/a
-b/a=10
b=-10a c/a=-2
c=-2a
$\frac{(a^2 + b^2 + c^2)}{(a + b + c)}$
=$\frac{(a^2 + (-10a)^2 + (-2a)^2)}{(a -10a -2a)}$
=$\frac{(105(a)^2)}{( -11a)}$
=$\frac{(-105(a))}{( 11)}$
7) Answer (C)
Let A, B and C receive Rs. $a,b,c$ respectively
Total amount = $a+b+c=60500$ ————-(i)
According to ques, => $a=\frac{2}{9}(b+c)$
=> $9a=2(60500-a)$ [Using equation (i)]
=> $9a=121000-2a$
=> $9a+2a=11a=121000$
=> $a=\frac{121000}{11}=Rs.$ $11000$
Similarly, $b=\frac{3}{7}(a+c)$
=> $7b=3(60500-b)$
=> $7b+3b=10b=181500$
=> $b=Rs.$ $18150$
$\therefore$ C’s share = $60500-11000-18150=Rs.$ $31350$
=> Ans – (C)
8) Answer (C)
Area of square = $ a^2 $
a = side of the square
given area of the square = 121 $cm^{2}$
solving, a =11
same wire is bent in to the form of a circle
therefore, perimeter of the square = perimeter of the circle
perimeter of the square = 4a = $ 4 \times a = 44 cm $
44 = perimeter of the circle
$ 44 = 2 \times \frac{22}{7} \times r $
solving r = 7
area of the circle = $ \pi r^2 $
= $ \frac{22}{7} \times 7^2 $
= 154 $cm^{2}$
9) Answer (B)
It is given that $\triangle$ ABC and $\triangle$ DEF are equiangular triangles, thus corresponding angles are equal.
=> $\triangle$ ABC $\sim\triangle$ DEF
=> Ratio of perimeter = $\frac{AB}{DE}=$ $\frac{BC}{EF}=$ $\frac{AC}{DF}$ ————-(i)
Since, AL and DM are medians, => Ratio of perimeter of $\triangle$ ABC to $\triangle$ DEF = $\frac{AL}{DM}$ ———–(ii)
From, equations (i) and (ii), we get :
=> $\frac{BC}{EF}=\frac{AL}{DM}$
=> Ans – (B)
10) Answer (A)
Let cost price of the article = Rs. $100$
=> Marked price = $100+(\frac{40}{100}\times100)$
= $100+40=Rs.$ $140$
Discount % = 40%
=> Selling price = $140-(\frac{40}{100}\times140)$
= $140-56=Rs.$ $84$
$\therefore$ Loss % = $\frac{(100-84)}{100}\times100=16\%$
=> Ans – (A)
Get 200 SSC mocks for just Rs. 249. Enroll here
We hope this Expected Maths Questions for SSC CGL Exams will be highly useful for your preparation.
