Cylinder Questions for CAT PDF
Download important CAT Cylinder Questions with Solutions PDF based on previously asked questions in CAT exam. Practice Cylinder Questions with Solutions for CAT exam.
Download Cylinder Questions for CAT PDF
Question 1: Consider a right circular cone of base radius 4 cm and height 10 cm. A cylinder is to be placed inside the cone with one of the flat surfaces resting on the base of the cone. Find the largest possible total surface area (in sq. cm) of the cylinder.
a) $\frac{100\pi}{3}$
b) $\frac{80\pi}{3}$
c) $\frac{120\pi}{7}$
d) $\frac{130\pi}{9}$
e) $\frac{110\pi}{7}$
Question 2: A solid metal cylinder of 10 cm height and 14 cm diameter is melted and re – cast into two cones in the proportion of 3 : 4 (volume), keeping the height 10 cm. What would be the percentage change in the flat surface area before and after?
a) 9%
b) 16%
c) 25%
d) 50%
e) None of the above
Question 3: A right circular cone is enveloping a right circular cylinder such that the base of the cylinder rests on the base of the cone. If the radius and the height of the cone is 4 cm and 10 cm respectively, then the largest possible curved surface area of the cylinder of radius r is:
a) $20πr^{2}$
b) $5πr(4 – r)$
c) $5πr(r – 4)$
d) $5πr(2 – r)$
Question 4: In a rocket shape firecracker, explosive powder is to be filled up inside the metallic enclosure. The metallic enclosure is made up of a cylindrical base and conical top with the base of radius 8 centimeter. The ratio of height of cylinder and cone is 5:3. A cylindrical hole is drilled through the metal solid with height one third the height of the metal solid. What should be the radius of the hole, so that volume of the hole (in which gun powder is to be filled up) is half of the volume of metal solid after drilling?
a) $4\sqrt{3}cm$
b) $4.0cm$
c) $3.0cm$
d) None of these
Question 5: A rectangular piece of paper is 22 cm. long and 10 cm. wide. A cylinder is formed by rolling the paper along its length. Find the volume of the cylinder.
a) 175 cm3
b) 180 cm3
c) 185 cm3
d) None of the above
Download CAT Quant Questions PDF
Question 6: Consider the volumes of the following objects and arrange them in decreasing order:
i. A parallelepiped of length 5 cm, breadth 3 cm and height 4 cm
ii. A cube of each side 4 cm.
iii. A cylinder of radius 3 cm and length 3 cm
iv. A sphere of radius 3 cm
a) iv,iii,ii,i
b) iv,ii,iii,i
c) iv,iii,i,ii
d) None of the above
Question 7: A 10 litre cylinder contains a mixture of water and sugar, the volume of sugar being 15% of total volume. A few litres of the mixture is released and an equal amount of water is added. Then the same amount of the mixture as before is released and replaced with water for a second time. As a result, the sugar content becomes 10% of total volume. What is the approximate quantity of mixture released each time?
a) 1 litres
b) 1.2 litres
c) 1.5 litres
d) 2 litres
Question 8: A right circular cylinder has a radius of 6 and a height of 24. A rectangular solid with a square base and a height of 20, is placed in the cylinder such that each of the corners of the solid is tangent to the cylinder wall. If water is then poured into the cylinder such that it reaches the rim, the volume of water is:
a) 288(π – 5)
b) 288(2π – 3)
c) 288(3π – 5)
d) None of the above
Question 9: A cylinder, a Hemi-sphere and a cone stand on the same base and have the same heights. The ratio of the areas of their curved surface is:
a) $2:2:1$
b) $2:\sqrt{2}:1$
c) $\sqrt{2}:3:1$
d) None of the above
Question 10: If a right circular cylinder of height 14 $cm$ is inscribed in a sphere of radius 8 $cm$, then the volume of the cylinder is:
a) 110 $cm^3$
b) 220 $cm^3$
c) 440 $cm^3$
d) 660 $cm^3$
Take a free CAT online mock test
Answers & Solutions:
1) Answer (A)
Trangle AGF and triangle FHC are similar.
So, $\frac{10-h}{x}=\frac{h}{4-x}$
=> $\frac{10-h}{h}=\frac{x}{4-x}$
=> $\frac{10}{h}-1=\frac{x}{4-x}$
=> $\frac{10}{h}=\frac{4}{4-x}$
=> $h=\frac{10}{4}(4-x)$
Total surface area= $2 \pi x^2 + 2 \pi x h= 2 \pi (x^2 + x \frac{10}{4}(4-x)=2 \pi (10x – \frac{3}{2} (x^2)=2 \pi (-\frac{3}{2}(x-\frac{10}{3}^{2})+ \frac{50}{3})$
This value will be maximum when the negative factor is minimum i.e. 0 because it is multiplied by a square. Thus, when x=10/3 the surface area is max.
So, the surface area is $\frac{100}{3} \pi$
2) Answer (D)
Volume of Cylinder = $\pi r^2 h = \pi \times 7^2 \times 10 = 490\pi$
Now, The solid metal cylinder is re-cast into two cones in the proportion 3 : 4 i.e. the volumes of cone 1 and cone 2 is
$210 \pi$ and $280 \pi$ respectively.
So, flat Surface area of cylinder before melting = $2 \pi r^2 = 2 \pi \times 7^2 = 98 \pi$
Volume of cone 1 = $\frac{1}{3} \pi r_1^2 h = 210 \pi$
=> $r_1^2 = \frac{210 \times 3}{10} = 63$
Volume of cone 2 = $\frac{1}{3} \pi r_2^2 h = 280 \pi$
=> $r_2^2 = \frac{280 \times 3}{10} = 84$
Flat surface area of cones = $\pi r_1^2 + \pi r_2^2$
= $\pi (63 + 84) = 147 \pi$
$\therefore$ Percentage change in surface area = $\frac{147 \pi – 98 \pi}{98 \pi} \times 100$
= $\frac{1}{2} \times 100 = 50 \%$
3) Answer (B)
Top face will look like the figure shown below.
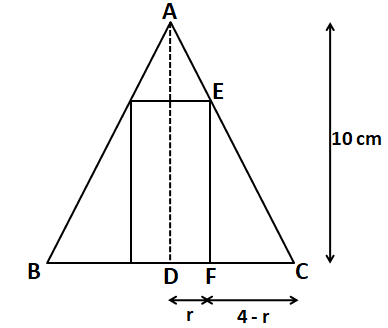
Curved surface area of the cylinder = $2*\pi*r*h$
To calculate height of the cylinder in terms of ‘r’, we can see that $\triangle$ADC is similar to $\triangle$EFC.
Therefore,
$\dfrac{AD}{DC}=\dfrac{EF}{FC}$
$\Rightarrow$ $\dfrac{10}{4} = \dfrac{h}{4-r}$
$\Rightarrow$ $h = \dfrac{5}{2}(4-r)$
Therefore, the curved surface area of the cylinder = $2*\pi*r*\dfrac{5}{2}(4-r)$ = $5πr(4 – r)$.
Hence, option B is the correct answer.
4) Answer (A)
Let us draw an appropriate diagram. Let us assume that ‘R’ is the radius of the hole.
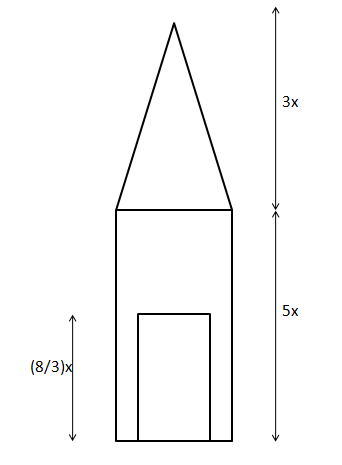
$\dfrac{1}{2}$*(Total volume – Volume of the hole) = Volume of the hole
Volume of the hole = $\dfrac{1}{3}*\text{Total volume of the rocket}$
$\pi*R^2*(8/3)x$ = $\dfrac{1}{3}*(\pi*8^2*5x+\dfrac{1}{3}*\pi*8^2*3x)$
$R^2*(8/3)$ = $\dfrac{1}{3}*(8^2*5+\dfrac{1}{3}*8^2*3)$
$R^2 = 48$
$R$ = $4\sqrt{3}$ cm. Hence, option A is the correct answer.
5) Answer (D)
When the paper is rolled along its length, the circumference of the cylinder formed is equal to the length and the height is equal to the breadth of the rectangle.
Let ‘r’ be the radius and ‘h’ be the height of the cylinder formed.
$2\pi*r = 22$ and h = 10
Hence, the volume of the cylinder = $\pi*r^2*h$ = $\dfrac{22}{7}*(7/2)^2*10$ = 385 $cm^3$.
6) Answer (A)
i. Volume of the parallelepiped of length 5 cm, breadth 3 cm and height 4 cm = 3*4*5 = 60 cm$^3$
ii. Volume of the cube of each side 4 cm = 4^3 = 64 cm$^3$
iii.Volume of the cylinder of radius 3 cm and length 3 cm = $\pi*3^2*3$ = 84.82 cm$^3$
iv. Volume of the sphere of radius 3 cm = $4/3*\pi*3^3$ = 113.09 cm$^3$
Therefore, we can say that volumes of the objects in decreasing order = iv,iii,ii,i.
Hence, option A is the correct answer.
7) Answer (D)
Initially in the 10L solution there is 1.5L sugar and 8.5L water.
We know that:-
Final volume of sugar = Initial volume of sugar*(Volume of solution that is not drawn out/total volume of solution)$^n$
i.e $1 = 1.5*(\dfrac{10-x}{10})^2$ Where x is the volume of the solution drawn out.
Thus, $200 = 3*(10^2 – 20x + x^2)$
Solving we get x $\approx 1.873$
The closest value in the option is option D.
Thus, option D is the correct answer.
8) Answer (C)
It is given that the radius of cylinder = 6 cm. The rectangular solid with a square base is placed in the cylinder such that each of the corners of the solid is tangent to the cylinder wall.
Therefore, the diagonal of square base = the diameter of circular base
Hence, a$\sqrt{2}$ = 2*6 = 12 => a = $6\sqrt{2}$ cm.
The volume of water = Volume of the cylinder – Volume of the rectangular solid
$\Rightarrow$ $\pi*6^2*24$ – $(6\sqrt{2})^2*20$
$\Rightarrow$ $864*\pi – 1440$
$\Rightarrow$ $288(3\pi – 5)$
9) Answer (D)
The cylinder, hemisphere and cone stand on the same base and have the same height. Let the radius of the three solids be $r$ and the height be $h$.
Height of the hemisphere, $h$ = $r$ (Radius)
Curved surface area of the cylinder = $2*\pi*r*r$ = $2*\pi*r^2$
Curved surface area of the hemisphere = $2*\pi*r^2$
Curved surface area of the cone = $\pi*r*\sqrt{r^2+r^2}$ = $\pi*r*\sqrt{r^2+r^2}$ = $\pi*r^2*\sqrt{2}$
Ratio = $2:2:\sqrt{2}$ = $\sqrt{2}:\sqrt{2}:1$
As the answer is not among the given options, option D is the right answer.
10) Answer (D)
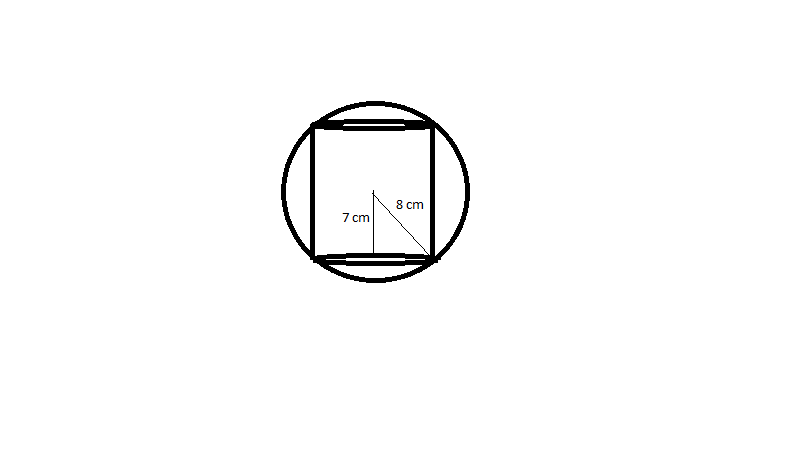
The radius of sphere is 8 $cm$. Then applying Pythagoras, the radius of base of cylinder is $\sqrt{15}$ $cm$
The height of cylinder is given as 14 $cm$. Volume of cylinder is $\pi$ $r^{2}$h
$\frac{22}{7}$* 15*14 = 660 $cm^3$
Download CAT Previous Papers PDF
Download Free CAT Preparation App
We hope this CAT Cylinder Questions with Solutions PDF for CAT will be helpful to you.
