Coordinate Geometry Questions for NMAT – Download PDF

Coordinate Geometry Questions for NMAT PDF:

Download Coordinate Geometry Questions for NMAT PDF. Top 10 very important Coordinate Geometry Questions for NMAT based on asked questions in previous exam papers.

Download Coordinate Geometry Questions for NMAT

Get 5 NMAT Mocks for Rs. 499

Take NMAT mock test

Question 1: Let P be the point of intersection of the lines
3x + 4y = 2a and 7x + 2y = 2018
and Q the point of intersection of the lines
3x + 4y = 2018 and 5x + 3y = 1
If the line through P and Q has slope 2, the value of a is:

a) 4035

b) 1/2

c) 3026

d) 1

e) 1009

Question 2: In a triangle ABC, medians AD and BE are perpendicular to each other, and have lengths 12 cm and 9 cm, respectively. Then, the area of triangle ABC, in sq cm, is

a) 78

b) 80

c) 72

d) 68

Question 3: A parallelogram ABCD has area 48 sqcm. If the length of CD is 8 cm and that of AD is s cm, then which one of the following is necessarily true?

a) $s≠6$

b) $s \geq 6$

c) $5 \leq s \leq 7$

d) $s \leq 6$

Question 4: If three sides of a rectangular park have a total length 400 ft, then the area of the park is maximum when the length (in ft) of its longer side is

Question 5: Let P$_{1}$ be the circle of radius R. A square Q$_{1}$ is inscribed in P$_{1}$ such that all the vertices of the square Q$_{1}$ lie on the circumference of P$_{1}$. Another circle P$_{2}$ is inscribed in Q$_{1}$. Another Square Q$_{2}$ is inscribed in the circle P$_{2}$. Circle P$_{3}$ is inscribed in the square Q$_{2}$ and so on. If S$_{N}$ is the area between Q$_{N}$ and P$_{N+1}$, where N represents the set of natural numbers, then the ratio of sum of all such S$_{N}$ to that of the area of the square Q$_{1}$ is :

a) $\dfrac{4 – \pi}{2}$

b) $\dfrac{2 \pi – 4}{\pi}$

c) $\dfrac{\pi – 2}{2}$

d) None of the above

Question 6: The coordinates of a triangle ABC are A(1, 5), B(-2, 3), and C(0,-4); find the equation of the median AD? ·

a) 7x-3y+-8= 0

b) 5x-4y+15=O

c) x+3y-16=0

d) 11x-4y+9=0

Question 7: Consider a triangle drawn on the X-Y plane with its three vertices at (41, 0), (0, 41) and (0, 0), each vertex being represented by its (X,Y) coordinates. The number of points with integer coordinates inside the triangle (excluding all the points on the boundary) is

a) 780

b) 800

c) 820

d) 741

Question 8: Two diagonals of a parallelogram intersect each other at coordinates (17.5, 23.5). Two adjacent points of the parallelogram are (5.5, 7.5) and (13.5, 16). Find the lengths of the diagonals.

a) 15 and 30

b) 15 and 40

c) 17 and 30

d) 17 and 40

e) Multiple solutions are possible

Question 9: From an interior point of an equilateral triangle, perpendiculars are drawn on all three sides. The sum of the lengths of the three perpendiculars is s. Then the area of the triangle is

a) $\frac{\sqrt{3}s^{2}}{2}$

b) $\frac{2s^{2}}{\sqrt{3}}$

c) $\frac{s^{2}}{2\sqrt{3}}$

d) $\frac{s^{2}}{\sqrt{3}}$

Question 10: ln a plane rectangular coordinate system, points L, M, N and O are represented by the coordinates (-5, 0), (1,-1), (0, 5), and (-1, 5) respectively. Consider a variable point P in the same plane. The minimum value of PL + PM + PN + PO is

a) $1+\sqrt{37}$

b) $5\sqrt{2}+2\sqrt{10}$

c) $\sqrt{41}+\sqrt{37}$

d) $\sqrt{41}+1$

e) None of these

Join 7K MBA Aspirants Telegram Group

Download Highly Rated CAT preparation App

Answers & Solutions:

1) Answer (C)

On solving for x and y from the equations

3x + 4y = 2018 and 5x + 3y = 1

we get Q(-550,917)

Let, P(x,y)

So, $\frac{y – 917}{x + 550}$ = 2

=> y – 2x = 2017 ….(1)

Considering the equations

3x + 4y = 2a ……..(2)

7x + 2y = 2018 …..(3)

On subtracting equation (2) from (3) we have,

4x – 2y = 2018 – 2a

=> 2x – y = 1009 – a

=> y – 2x = a -1009 …..(4)

From equation (1) and (4)

2017 = a – 1009

=> a = 3026

Hence, option C.

2) Answer (C)

It is given that AD and BE are medians which are perpendicular to each other.

The lengths of AD and BE are 12cm and 9cm respectively.

It is known that the centroid G divides the median in the ratio of 2:1

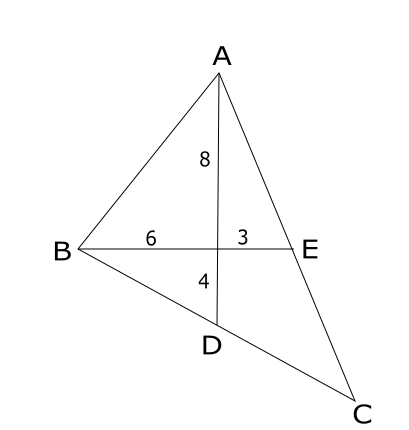
Area of $\triangle$ ABC = 2* Area of the triangle ABD

Area of $\triangle\ $ABD = Area of $\triangle\ $ AGB + Area of $\triangle\ $ BGD

Since $\angle\ AGB\ =\ \angle\ BGD\ =\ 90$ (Given)

Area of $\triangle\ $ AGB = $\ \frac{\ 1}{2}\times\ 8\times\ 6$ = 24

Area of $\triangle\ $ BGD = $\ \frac{\ 1}{2}\times\ 6\times\ 4$ = 12

Area of $\triangle\ $ABD = 24+12=36

Area of $\triangle\ ABC\ =\ 2\times\ 36=72$

3) Answer (B)

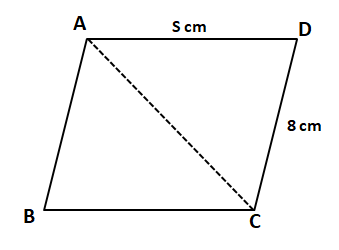
We can see that area of parallelogram ABCD = 2*Area of triangle ACD

48 = 2*Area of triangle ACD

Area of triangle ACD = 24

$(1/2)*CD*DA*sinADC=24$

$AD*sinADC=6$

We know that $sin\theta$ $\leq$ 1, Hence, we can say that AD $\geq$ 6

$\Rightarrow$ s $\geq$ 6

4) Answer: 200

Let the length and breadth of the park be l,b, l > b
Case 1: 2l + b = 400
Area = lb. Area is maximum when 2l * b is maximum, which is maximum when 2l = b (using AM $ \geq $ GM inequality) => l = 100, b = 200. Which can’t happen since l > b

Case 2: l + 2b = 400
Area = lb. Area is maximum when l *2 b is
maximum, which is maximum when l = 2b (using AM $ \geq $ GM
inequality) => l = 200, b = 100.

Hence length of the longer side is 200 ft

5) Answer (A)

Let us draw the diagram according to the information given,

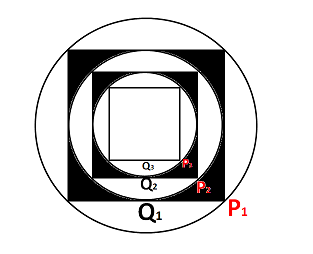
There will be infinite shaded areas as shown in the figure.

Area of circle P$_{1}$ = $\pi*R^2$

Area of square Q$_{1}$ = $(\sqrt{2}*R)^2$ = $2R^2$

Area of circle P$_{2}$ = $\pi*(\dfrac{R}{\sqrt{2}})^2=\pi*R^2/2$

Area of square Q$_{2}$ = $R^2$

Area of circle P$_{3}$ = $\pi*(\dfrac{R}{2})^2=\pi*R^2/4$

Therefore, S$_{N}$ = [$2R^2-\pi*\dfrac{R^2}{2}$]+[$R^2-\pi*\dfrac{R^2}{4}$]+…

S$_{N}$ = $(2R^2+R^2+\dfrac{R^2}{2}+… )$- $(\pi*\dfrac{R^2}{2}+\pi*\dfrac{R^2}{4}+\pi*\dfrac{R^2}{8}…)$

S$_{N}$ = $4R^2-\pi*R^2$

Therefore, $\dfrac{S_{N}}{Q_{1}}$ = $\dfrac{4R^2-\pi*R^2}{2R^2}$ = $\dfrac{4 – \pi}{2}$. Hence, option A is the correct answer.

6) Answer (D)

Given that $\triangle$ABC

Since AD is the median to BC, D will be mid point of BC. So coordinates of D = ($\frac{-2+0}{2} ,\frac{3-4}{2}$) = (-1 ,$\frac{-1}{2}$)

Equation of line passing through points A(1,5) and D(-1,$\frac{-1}{2}$) will be :

$(y-x_{1})=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})$                   (Here $(x_{1},y_{1})=(1,5)$ ,  $(x_{2},y_{2})=(-1,\frac{-1}{2})$)

$(y-5)=\frac{(\frac{-1}{2})-(5)}{(-1)-(1)}(x-1)$

$4(y-5)=11(x-1)$

$11x-4y+9=0$

7) Answer (A)

The number of points on x = 1 is 39. The number of points on x = 2 is 38 and so on till x = 39, which has one point.

So, the total is 1+2+3+…+39 = $\frac{39*40}{2}$ = 780.

8) Answer (D)

Using distance formula,

$CX = \sqrt{(17.5 – 5.5)^2 + (23.5 – 7.5)^2} = \sqrt{12^2 + 16^2}$

= $\sqrt{144 + 256} = \sqrt{400} = 20$

=> $AC = 2 \times CX = 40$

$BX = \sqrt{(17.5 – 13.5)^2 + (23.5 – 16)^2} = \sqrt{4^2 + 7.5^2}$

= $\sqrt{16 + 56.25} = \sqrt{72.25} = 8.5$

=> $BD = 2 \times BX = 17$

9) Answer (D)

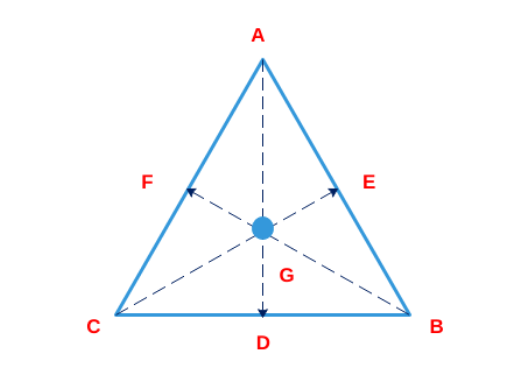
Based on the question: AD, CE and BF are the three altitudes of the triangle. It has been stated that {GD+GE+GF = s}

Now since the triangle is equilateral, let the length of each side be “a”. So area of triangle will be

$\frac{1}{2}\times\ GD\times\ a+\ \frac{1}{2}\times\ GE\times\ a\ +\frac{1}{2}\times\ GF\times\ a=\frac{\sqrt{\ 3}}{4}a^2$

Now $GD+GE+GF=\frac{\sqrt{\ 3}a}{2}$ or $s=\frac{\sqrt{\ 3}a}{2}\ or\ a=\frac{2s}{\sqrt{\ 3}}$

Given the area of the equilateral triangle = $\ \frac{\sqrt{3}}{4}a^2\ $ ; substituting the value of ‘a’ from above, we get the area {in terms ‘s’}= $\frac{s^2}{\sqrt{3}}$

10) Answer (B)

$(PL + PN)$ will be minimum if P lies on LN, and $(PM + PO)$ will be minimum if P lies on OM.

=> P must be the intersection point of the diagonals of the quadrilateral.

$\therefore$ Min (PL + PM + PN + PO)

= $LN + OM$

= $(\sqrt{(0 + 5)^2 + (5 – 0)^2}) + (\sqrt{(1 + 1)^2 + (-1 – 5)^2})$

= $(\sqrt{25 + 25}) + (\sqrt{4 + 36})$

= $\sqrt{50} + \sqrt{40} = 5 \sqrt{2} + 2 \sqrt{10}$

Get 5 NMAT Mocks for Rs. 499

We hope this Coordinate Geometry Questions for NMAT pdf for NMAT exam will be highly useful for your Preparation.