Cone Questions for NMAT:
Download Cone Questions for NMAT PDF. Top 10 very important Cone Questions for NMAT based on asked questions in previous exam papers.
Download Cone Questions for NMAT
Take NMAT mock test
Question 1: The base radius of a frustum of a cone is 10 cm and the top radius is 5 cm and height 10 cm. What is ratio of the volume of the frustum to the volume of the original cone?
a) 7:8
b) 8:9
c) 9:10
d) 2:3
Question 2: Diameter of the base of a water-filled inverted right circular cone is 26 cm. A cylindrical pipe, 5 mm in radius, is attached to the surface of the cone at a point. The perpendicular distance between the point and the base (the top) is 15 cm. The distance from the edge of the base to the point is 17 cm, along the surface. If water flows at the rate of 10 meters per minute through the pipe, how much time would elapse before water stops coming out of the pipe?
a) < 4 minutes
b) > 4.0 minutes but < 4.5 minutes
c) > 4.5 minutes but < 5.0 minutes
d) > 5.0 minutes but < 6 minutes
e) > 6 minutes
Question 3: A solid right circular cone of height 12cm and base radius of 9cm is cut at the top to form a frustum. The cut part is melted and used completely to form a sphere of radius 3cm. What is the height of the frustum?
a) $4\sqrt[3]{3}$
b) $3\sqrt[3]{3}$
c) None of the above
d) Can’t be determined
Question 4: Two right circular cones are such that their base areas are in the ratio 16:9 and their curved surface areas are in the ratio 1:2, find the ratio of their slant heights.
a) 1:3
b) 3:8
c) 8:3
d) 3:4
Question 5: There is a right circular cone of base radius 10 cm. A portion of the cone is cut off to form another right circular cone of radius 5 cm. Find the ratio of the curved surface area of the frustum to the curved surface area of the smaller cone. ( $\pi = 22/7 $)
a) 7:5
b) 2:1
c) 3:1
d) 3:2
Join 7K MBA Aspirants Telegram Group
Download Highly Rated CAT preparation App
Answers & Solutions:
1) Answer (A)
Let the height of the small cone(the portion that is lost when the big cone is cut to make the frustum) be ‘h’
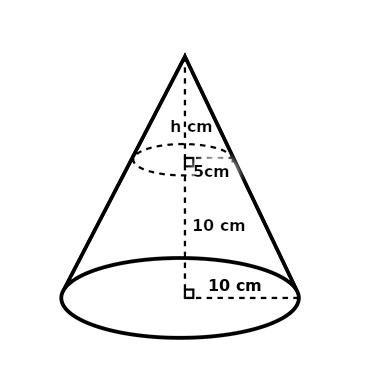
Since the triangles are similar, 5/h = 10/(10+h) => 50 + 5h = 10h => h = 10
Volume of the big cone = $(1/3) \pi * 10^2 * (10+10)$
Volume of the small cone = $(1/3) \pi * 5^2 * 10$
Volume of the frustum = (1/3)* ($\pi * 10^2 * 20$ – $\pi * 5^2 * 10$)
So, required ratio = 1750/2000 = 7:8
2) Answer (D)
We can make the following figure:

time it will take is $1295/250 = 5.18$Height of the cone= 13/5=h/(h-15)
13h-195= 5h
h=195/8
Volume of water that will come out
=$\frac{1}{3}\pi\ \left[R_1^2\ \left(H_1\right)-R_2^2\left(H_2\right)\right]$
=$\frac{1}{3}\pi\ \left[13_{ }^2\ \left(\frac{195}{8}\right)-5^2\left(\frac{75}{8}\right)\right]$
= $1295\pi$
Rate at which the water will come out is = $\pi\ \left(0.5\right)^2\times\ 1000\ cm^3$/min=$250\pi$.
So, the amount of time it will take is $1295/250 = 5.18$min
3) Answer (C)
The volume of the cut part=volume of sphere = $(4/3)\pi (3^3)$ = $36 \pi$.
Hence, the volume of the cut-out cone is $36 \pi$.
Let h be the height of the cut-out cone and r be the radius of the base.
Hence, $h/r = 12/9 => h=4/3 r$.
Thus, the volume of cut-out cone $= (\pi)/3 * r^2 * (4/3) r = 36 \pi$
So, $r^3 = 81$
So, $r = 3\sqrt [3]{3}$. Hence $h = 4\sqrt[3]{3}$.
Hence, length of frustum $h_f= 12 – 4\sqrt[3]{3}$.
Hence, correct option is none of the above.
4) Answer (B)
Base areas are in the ratio 16:9 => Base radii are in the ratio 4:3.
Curved surface areas are in the ratio 1:2.
So, $\frac{\pi * 4r * l_1}{\pi 3r*l_2} = \frac{1}{2}$
So, $l_1:l_2 = 3:8$
5) Answer (C)

The radius of the smaller cone is 5 cm.
The slant height = x.
Therefore, the curved surface area of the smaller cone = $\pi*5*x$.
By similar triangles, x/5 = (x+l)/10
10x = 5x+5l
5x = 5l
x = l
The radii of the frustum are 10 cm and 5 cm.
Curved surface area of small cone =$\pi r x$ = $5\pi x$
Curved surface area of original cone = $10\pi (x+l)$ = $10\pi (x+x)$ = $20\pi x$
Curved surface area of frustum = $20\pi x$ – $5\pi x$ =$15\pi x$
Ratio = $15\pi x$/$5\pi x$ = 3:1
We hope this Cone Questions for NMAT pdf for NMAT exam will be highly useful for your Preparation.






