CAT Triangles and Circles (Geometry) Questions PDF

Triangles and Circles questions are important concepts in the Geometry concept of the CAT Quant section. These questions are not very tough; make sure you are aware of all the Important Formulas in CAT Geometry. Solve more questions from CAT Triangles and Circles. You can check out these CAT Geometry questions from the CAT Previous year papers. Practice a good number of questions in CAT Geometry – Triangles and Circles so that you can answer these questions with ease in the exam. In this post, we will look into some important CAT Geometry Questions. These are a good source of practice for CAT 2022 preparation; If you want to practice these questions, you can download these Important Triangles and Circles (Geometry) Questions for CAT (with detailed answers) PDF along with the video solutions below, which is completely Free.

Download Triangles and Circles (Geometry) Questions for CAT

Enroll for CAT 2022 Online Course

Question 1: In a triangle ABC, the lengths of the sides AB and AC equal 17.5 cm and 9 cm respectively. Let D be a point on the line segment BC such that AD is perpendicular to BC. If AD = 3 cm, then what is the radius (in cm) of the circle circumscribing the triangle ABC?

a) 17.05

b) 27.85

c) 22.45

d) 32.25

e) 26.25

1) Answer (E)

View Video Solution

Solution:

Let x be the value of third side of the triangle. Now we know that Area = 17.5*9*x/(4*R), where R is circumradius.

Also Area = 0.5*x*3 .

Equating both, we have 3 = 17.5*9 / (2*R)

=> R = 26.25.

Question 2: Consider obtuse-angled triangles with sides 8 cm, 15 cm and x cm. If x is an integer then how many such triangles exist?

a) 5

b) 21

c) 10

d) 15

e) 14

2) Answer (C)

View Video Solution

Solution:

For obtuse-angles triangle, $c^2 > a^2 + b^2$ and c < a+b
If 15 is the greatest side, 8+x > 15 => x > 7 and $225 > 64 + x^2$ => $x^2$ < 161 => x <= 12
So, x = 8, 9, 10, 11, 12
If x is the greatest side, then 8 + 15 > x => x < 23
$x^2 > 225 + 64 = 289$ => x > 17
So, x = 18, 19, 20, 21, 22
So, the number of possibilities is 10

Question 3: Two circles, both of radii 1 cm, intersect such that the circumference of each one passes through the centre of the other. What is the area (in sq. cm.) of the intersecting region?

a) $\frac{\pi}{3}-\frac{\sqrt 3}{4}$

b) $\frac{2\pi}{3}+\frac{\sqrt 3}{2}$

c) $\frac{4\pi}{3}-\frac{\sqrt 3}{2}$

d) $\frac{4\pi}{3}+\frac{\sqrt 3}{2}$

e) $\frac{2\pi}{3}-\frac{\sqrt 3}{2}$

3) Answer (E)

View Video Solution

Solution:

The circumferences of the two circle pass through each other’s centers. Hence, O1A = O1B=O1O2 = 1cm

By symmetry, the line joining the two centres would be bisect AB and would be bisected by AB. As the line joining the center to the midpoint of a chord is perpendicular to the chord, O1O2 and AB are perpendicular bisectors of each other. Suppose they intersect at point P.

O1P = Half of O1O2 = 1/2 cm
So, the angle AO1P = 60 degrees as cos 60 = 1/2
By symmetry, BO1P = 60 degrees.
So, angle AO1B= 120 degrees

In the above, the required area is 2 times A(segment ABO2)(blue region). And A(segment ABO2)(blue region) = A(sector O2AO1B)(blue + red) – A(triangleO1AB )(red)

Area of sector = 120°/360° * $\pi * 1^2 $ = $\pi/3$

Area of triangle = 1/2 * b * h = 1/2 * (2* 1 cos 30°) * (1/2) = √3/4

Hence, required area = $\frac{\pi}{3}-\frac{\sqrt 3}{4}$ . Hence so the required area is 2 times the above value which is $\frac{2\pi}{3}-\frac{\sqrt 3}{2}$

Question 4: In the figure below, AB is the chord of a circle with center O. AB is extended to C such that BC = OB. The straight line CO is produced to meet the circle at D. If $\angle{ACD}$ = y degrees and $\angle{AOD}$ = x degrees such that x = ky, then the value of k is

a) 3

b) 2

c) 1

d) None of the above.

4) Answer (A)

View Video Solution

Solution:

Since Angle BOC = Angle BCO = y.

Angle OBC = 180-2y .

Hence Angle ABO =  z = 2y = Angle OAB.

Now since x is exterior angle of triangle AOC .

We have x = z + y = 3y.

Hence option A.

Question 5: 
In the adjoining figure, chord ED is parallel to the diameter AC of the circle. If angle CBE = 65°, then what is the value of angle DEC?

a) 35

b) 55

c) 45

d) 25

5) Answer (D)

View Video Solution

Solution:

If EBC = 65 then EOC = 130 then OEC = OCE = 25. NOw since OC and ED are parallel we have OCE = OED = 25. Hence option D.

Checkout: CAT Free Practice Questions and Videos

Question 6: What is the distance in cm between two parallel chords of lengths 32 cm and 24 cm in a circle of radius 20 cm?

a) 1 or 7

b) 2 or 14

c) 3 or 21

d) 4 or 28

6) Answer (D)

View Video Solution

Solution:

The distances of the chords from the center are 12 cm and 16 cm respectively.

If the chords lie on the same side of the center, the distance between the chords is 4 cm, if they lie on opposite sides of the center, the distance between them is 28 cm.

Question 7: Two identical circles intersect so that their centres, and the points at which they intersect, form a square of side 1 cm. The area in sq. cm of the portion that is common to the two circles is

a) $\pi$/4

b) $\pi$/2-1

c) $\pi$/5

d) $\sqrt\pi-1$

7) Answer (B)

View Video Solution

Solution:

We know that quad ambn is a square of side 1.

Area of the sector a-mqn is $\frac{90}{360}* \pi *1*1$ = $\frac{\pi }{4}$.

Area of square = 1*1 = 1

Area of common portion = 2 * Area of sector – Area of square

= 2 * $\frac{\pi }{4}$ – 1 =  $\frac{\pi }{2}$ – 1

Question 8: In the following figure, the diameter of the circle is 3 cm. AB and MN are two diameters such that MN is perpendicular to AB. In addition, CG is perpendicular to AB such that AE:EB = 1:2, and DF is perpendicular to MN such that NL:LM = 1:2. The length of DH in cm is

a) $2\sqrt2 – 1$

b) $(2\sqrt2 – 1)/2$

c) $(3\sqrt2 – 1)/2$

d) $(2\sqrt2 – 1)/3$

8) Answer (B)

View Video Solution

Solution:

Let EO = x, So, AE = 1.5 – x
AE : EB = 1:2 => x = 1/2

(1.5-x):(1.5+x) = 1:2.

x=0.5.

So, EO = 0.5
Similarly, OL = 0.5
Now, EOLH is a parallelogram and EO = OL = 0.5
In triangle DOL, DO = radius = 1.5 and OL = 0.5
So, DL = $\sqrt2$
=> DH = $(2\sqrt2 – 1)/2$

Question 9: In triangle DEF shown below, points A, B and C are taken on DE, DF and EF respectively such that EC = AC and CF = BC. If angle D equals 40 degress , then angle ACB is ?

a) 140

b) 70

c) 100

d) None of these

9) Answer (C)

View Video Solution

Solution:

Let angle EAC = x, so angle AEC = x and angle ACE = 180-2x
Let angle FBC = y, so angle BFC = y and angle BCF = 180-2y
So, angle ACB = 180-(180-2x+180-2y) = 2(x+y) – 180
x+y = 180 – 40 = 140
So, angle ACB = 280 – 180 = 100

Question 10: Consider a circle with unit radius. There are 7 adjacent sectors, S1, S2, S3,….., S7 in the circle such that their total area is (1/8)th of the area of the circle. Further, the area of the $j^{th}$ sector is twice that of the $(j-1)^{th}$ sector, for j=2, …… 7. What is the angle, in radians, subtended by the arc of S1 at the centre of the circle?

a) $\pi/508$

b) $\pi/2040$

c) $\pi/1016$

d) $\pi/1524$

10) Answer (A)

View Video Solution

Solution:

Now area of 1st sector = $\pi * r^2 * \frac{x}{360}$ where x – angle subtended at center

Now the next sector will have 2x as the angle, and similarly angles will be in GP with ratio = 2.

Sum of areas of all 7 sectors = $\frac{127*x* \pi * r^2}{360}$ which is equal to $\frac{\pi * r^2}{8}$

We get x = $\frac{360}{8*127}$

Now if converted in radians we get  x = $\pi/508$.

Question 11: If a,b,c are the sides of a triangle, and $a^2 + b^2 +c^2 = bc + ca + ab$, then the triangle is:

a) equilateral

b) isosceles

c) right angled

d) obtuse angled

11) Answer (A)

View Video Solution

Solution:

$(a+b+c)^2 = a^2 + b^2 + c^2 + 2(ab + bc + ca) => 3(a^2 + b^2 + c^2)$

This is possible only if a = b = c.

So, the triangle is an equilateral triangle.

Question 12: In the figure given below, ABCD is a rectangle. The area of the isosceles right triangle ABE = 7 $cm^2$ ; EC = 3(BE). The area of ABCD (in $cm^2$) is

a) 21 $cm^2$

b) 28 $cm^2$

c) 42 $cm^2$

d) 56 $cm^2$

12) Answer (D)

View Video Solution

Solution:

Let AB = BE = x

Area of triangle ABE = $x^2/2$ = 14; we get x = $\sqrt{14}$

So we have side BC = 4*$\sqrt{14}$

Now area is AB*BC = 14 *4 = 56 $cm^2$

Question 13: The area of the triangle whose vertices are (a,a), (a + 1, a + 1) and (a + 2, a) is
[CAT 2002]

a) $a^3$

b) $1$

c) $2a$

d) $2^{1/2}$

13) Answer (B)

View Video Solution

Solution:

The triangle we have is :

The length of three sides is $\sqrt 2, \sqrt 2$ and $2$.
This is a right-angled triangle.
Hence, it’s area equals $1/2 * \sqrt 2 * \sqrt 2 = 1$
So, the correct answer is b)
Alternate Approach :
Area of triangle = $\frac{1}{2}\times\ base\times\ height$
So we get $\frac{1}{2}\times2\times\ 1$=1 square units

Question 14: In the following figure, ACB is a right-angled triangle. AD is the altitude. Circles are inscribed within the triangle ACD and triangle BCD. P and Q are the centers of the circles. The distance PQ is

The length of AB is 15 m and AC is 20 m

a) 7 m

b) 4.5 m

c) 10.5 m

d) 6 m

14) Answer (A)

View Video Solution

Solution:

By Pythagoras theorem we get BC = 25 . Let BD = x;Triangle ABD is similar to triangle CBA => AD/15 = x/20 and also triangle ADC is similar to triangle ACB=> AD/20 = (25-x)/15. From the 2 equations, we get x = 9 and DC = 16

We know that AREA = (semi perimeter ) * inradius

For triangle ABD, Area = 1/2 x BD X AD = 1/2 x 12 x 9 = 54 and semi perimeter = (15 + 9 + 12)/2 = 18. On using the above equation we get, inradius, r = 3.

Similarly for triangle ADC we get inradius R = 4 .

PQ = R + r = 7 cm

Question 15: A circle is inscribed in a given square and another circle is circumscribed about the square. What is the ratio of the area of the inscribed circle to that of the circumscribed circle?

a) 2 : 3

b) 3 : 4

c) 1 : 4

d) 1 : 2

15) Answer (D)

View Video Solution

Solution:

As we know that area of the circle is directly proportional to the square of its radius.
Hence $\frac{A_{ic}}{A_{cc}} = \frac{\frac{x^2}{4}}{\frac{x^2}{2}}$
Where $x$ is side of square (say), ic is inscribed circle with radius $\frac{x}{2}$, cc is circumscribed circle with radius $\frac{x}{\sqrt{2}}$
So ratio will be 1:2

Question 16: If ABCD is a square and BCE is an equilateral triangle, what is the measure of ∠DEC?

a) 15°

b) 30°

c) 20°

d) 45°

16) Answer (A)

View Video Solution

Solution:

According to given diagram, as triangle BCE is equilateral CE=BE=DC
Hence angle CDE = angle CED

So angle DEC = $\frac{180-150}{2} = 15$
Question 17: In triangleABC, ∠B is a right angle, AC = 6 cm, and D is the mid-point of AC. The length of BD is

a) 4cm

b) 6 cm

c) 3cm

d) 3.5cm

17) Answer (C)

View Video Solution

Solution:

A circle is circumscribed to triangle ABC.

For this circle D will be centre of circle, and AD , DC , BD will radius of this circle.

Hence AD=BD=DC=3 cm

Question 18: The sum of the areas of two circles, which touch each other externally, is $153\pi$. If the sum of their radii is 15, find the ratio of the larger to the smaller radius.

a) 4

b) 2

c) 3

d) None of these

18) Answer (A)

View Video Solution

Solution:

Given:
$\pi((r_1)^2 + (r_2)^2) = 153\pi$
So
$(r_1)^2 + (r_2)^2 = 153$
Or $((r_1) + (r_2))^2 – 2(r_1)(r_2) = 153$
Or  $(r_1)(r_2) = 36$ and $(r_1) + (r_2) = 15$
$r_1 = 12$
$r_2 = 3$
Ratio = 4

Question 19: 
AB is the diameter of the given circle, while points C and D lie on the circumference as shown. If AB is 15 cm, AC is 12 cm and BD is 9 cm, find the area of the quadrilateral ACBD.

a) 54sq. cm

b) 216sq. cm

c) 162sq. cm

d) None of these

19) Answer (D)

View Video Solution

Solution:

Since ACBD is cyclic quadrilateral with diagonals as AB = 15 ad CD.
So area = $\frac{1}{2} \times (AB) \times (CD)$                  eq.(1)
Triangle ACB and ABD is right angled triangle
Let’s say angle CBA = $\theta$
so $CD = 2 \times (9 sin\theta)$  (Where  $sin\theta$ = $\frac{12}{15}$)
CD = $\frac{72}{5}$
Putting values in eq. (1) , we will get area = 108 sq.cm.
Hence answer will be D)

Question 20: From a triangle ABC with sides of lengths 40 ft, 25 ft and 35 ft, a triangular portion GBC is cut off where G is the centroid of ABC. The area, in sq ft, of the remaining portion of triangle ABC is

a) $225\sqrt{3}$

b) $\frac{500}{\sqrt{3}}$

c) $\frac{275}{\sqrt{3}}$

d) $\frac{250}{\sqrt{3}}$

20) Answer (B)

View Video Solution

Solution:

The lengths are given as 40, 25 and 35.

The perimeter = 100

Semi-perimeter, s = 50

Area = $ \sqrt{50 * 10 * 25 * 15}$ = $250\sqrt{3}$

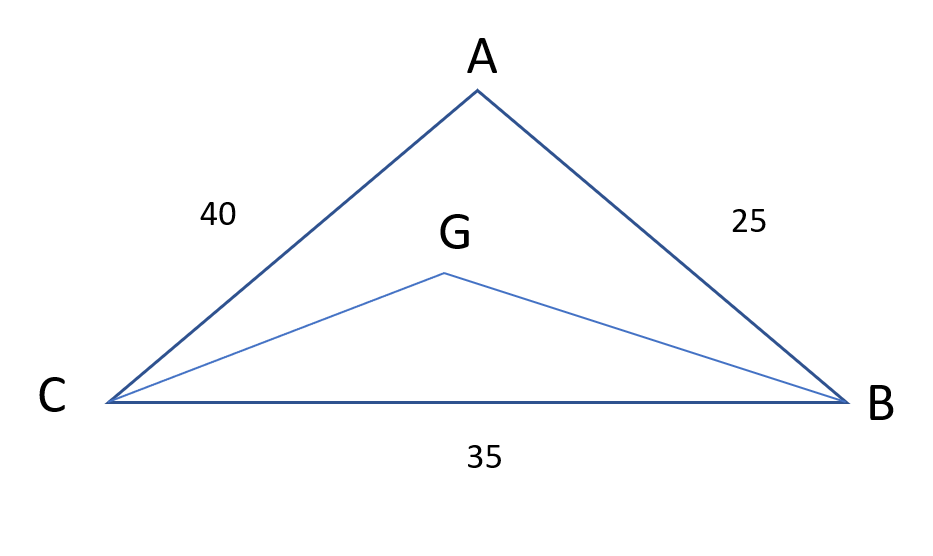
The triangle formed by the centroid and two vertices is removed.

Since the cenroid divides the median in the ratio 2 : 1

The remaining area will be two-thirds the area of the original triangle.

Remaining area = $\frac{2}{3} * 250\sqrt{3}$ = $\frac{500}{\sqrt{3}}$