CAT Set Theory and Venn Diagrams is one of the key topics in the CAT Quants and LRDI sections. CAT Set Theory and Venn Diagram questions appear in the CAT and other MBA entrance exams every year. You can check out these CAT Set Theory and Venn Diagram Questions from Previous years. In this article, we will look into some important CAT Set Theory and Venn Diagram Questions (with Notes) PDF. These are a good source for practice; If you want to practice these questions, you can download the CAT Set Theory and Venn Diagram Questions PDF, which is completely Free.
Download Important CAT Venn Diagram Questions+Notes
Enroll for CAT 2022 Online Course
- CAT Set theory and Venn Diagram Questions – Tip 1: Be thorough with all the basics of this topic. If you’re starting the prep, firstly understand the CAT Modern Maths Syllabus; CAT Venn Diagram questions are not very tough, and hence must not be avoided. This concept is particularly helpful for the CAT LRDI Section.
- CAT Set Theory and Venn Diagram Questions – Tip 2: Understand the important representations and formulas for the 2-set, 3-set and 4-set Venn diagrams.
- Practice these CAT Set Theory and Venn Diagram questions PDF. Learn all the major formulae from these concepts. You can check out the Important CAT Set Theory and Venn Diagram questions & Formulas PDF here.
Question 1: Shyam visited Ram during his brief vacation. In the mornings they both would go for yoga. In the evenings they would play tennis. To have more fun, they indulge only in one activity per day, i.e. either they went for yoga or played tennis each day. There were days when they were lazy and stayed home all day long. There were 24 mornings when they did nothing, 14 evenings when they stayed at home, and a total of 22 days when they did yoga or played tennis. For how many days Shyam stayed with Ram?
a) 32
b) 24
c) 30
d) None of these
1) Answer (C)
Solution:
Let the number of total days=N
They played tennis for=N-14 days
They did yoga for =N-24 days
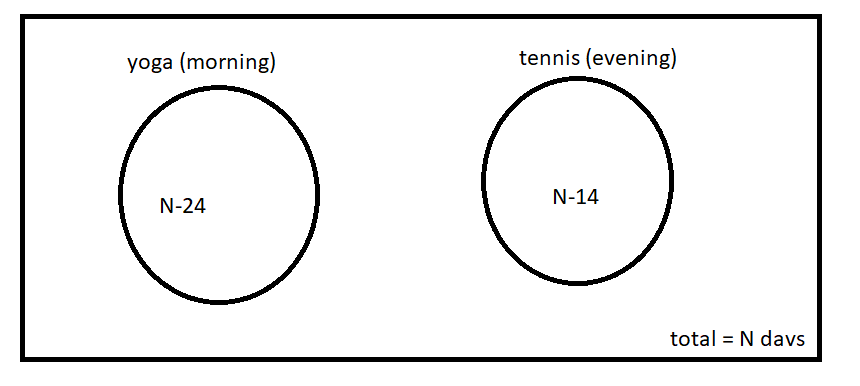
And the question says that total days when they did yoga or played tennis are 22
which means
N-14 + N-24 = 22
2N – 38 = 22
2N = 60
N = 30
Hence total days they stayed together were 30
Instructions
There were a hundred schools in a town. Of these, the number of schools having a play – ground was 30, and these schools had neither a library nor a laboratory. The number of schools having a laboratory alone was twice the number of those having a library only. The number of schools having a laboratory as well as a library was one-fourth the number of those having a laboratory alone. The number of schools having either a laboratory or a library or both was 35.
Question 2: How many schools had none of the three viz., laboratory, library or play – ground?
a) 20
b) 5
c) 30
d) 35
2) Answer (D)
Solution:

The diagram for this question has been shown:
Total number of schools having either or LAB or LIB or both = a+b+x/2 – y + y + 3x = 7x/2 + a + b = 35
Here a = b = y = 0
7x/2 = 35
x = 10
Total number of schools having at least one of PG, LIB or LAB = 30+2x+x+x/2 = 30+3x+x/2 = 30+30+5 = 65
Number of schools having neither of the three = 100-65 = 35
Question 3: What was the ratio of schools having laboratory those having library?
a) 1 : 2
b) 5 : 3
c) 2 : 1
d) 2 : 3
3) Answer (B)
Solution:

The diagram for this question has been shown:
Total number of schools having either or LAB or LIB or both = a+b+x/2 – y + y + 3x = 7x/2 + a + b = 35
It has been given that the schools having playground don’t have a Library or Laboratory.
Hence a = b = y = 0
7x/2 = 35
x = 10
Required ratio = 25:15 = 5:3
InstructionsA survey of 200 people in a community who watched at least one of the three channels — BBC, CNN and
DD — showed that 80% of the people watched DD, 22% watched BBC, and 15% watched CNN.
Question 4: What is the maximum percentage of people who can watch all the three channels?
a) 12.5%
b) 8.5%
c) 15%
d) Data insufficient
4) Answer (B)
Solution:
Let a be the number who watch only one channel, b be the number who watch only 2 channels and c be the number who watch all channels.
a+b+c = 100
a+2b+3c = 80+22+15 =117
Subtracting both equations,
b+2c = 117-100 = 17
Maximum c occurs when b = 0
2c = 17
c = 8.5
Question 5: If 5% of people watched DD and CNN, 10% watched DD and BBC, then what percentage of people watched BBC and CNN only?
a) 2%
b) 5%
c) 8.5%
d) Cannot be determined
5) Answer (A)
Solution:
Applying AUBUC formula
Let x be the number who watch BBC and CNN and y be the number who watch all three channels.
100 = 80+22+15-(10+5+x)+y
x-y = 2
Hence only 2% people watch BBC and CNN only.
Question 6: Referring to the previous question, what percentage of people watched all the three channels?
a) 3.5%
b) 0%
c) 8.5%
d) Cannot be determined
6) Answer (D)
Solution:
Applying AUBUC formula
Let x be the number who watch BBC and CNN and y be the number who watch all three channels.
100 = 80+22+15-(10+5+x)+y
x-y = 2
We cannot find the exact value of y.
Hence, the answer is “cannot be determined”.
Question 7: Each of 74 students in a class studies at least one of the three subjects H, E and P. Ten students study all three subjects, while twenty study H and E, but not P. Every student who studies P also studies H or E or both. If the number of students studying H equals that studying E, then the number of students studying H is
7) Answer: 52
Solution:
Let us draw a Venn diagram using the information present in the question.
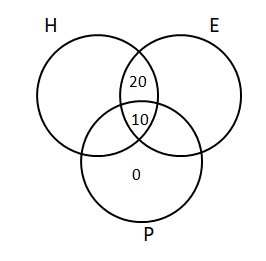
It is given that the number of students studying H equals that studying E.
Let ‘x’ be the total number of students who studied H, and H and P but mot E.We can also say that the same will be the number of students who studied E, and E and P but not H.Therefore,
x + 20 + 10 + x = 74
x = 22
Hence, the number of students studying H = 22 + 10+ 20 = 52
Question 8: If among 200 students, 105 like pizza and 134 like burger, then the number of students who like only burger can possibly be
a) 23
b) 26
c) 96
d) 93
8) Answer (D)
Solution:
It has been given that among 200 students, 105 like pizza and 134 like burger.
The question asks us to find out the number of students who can be liking only burgers among the given values.
The least number of students who like only burger will be obtained when everyone who likes pizza likes burger too.
In this case, 105 students will like pizza and burger and 134-105 = 29 students will like only burger. Therefore, the number of students who like only burger cannot be less than 29.
The maximum number of students who like only burger will be obtained when we try to separate the 2 sets as much as possible.
There are 200 students in total. 105 of them like pizza. Therefore, the remaining 95 students can like only burger and 134-95 = 39 students can like both pizza and burger. As we can see, the number of students who like burger cannot exceed 95.
The number of students who like only burger should lie between 29 and 95 (both the values are included).
93 is the only value among the given options that satisfies this condition and hence, option D is the right answer.
Question 9: For two sets A and B, let AΔB denote the set of elements which belong to A or B but not both. If P = {1,2,3,4}, Q = {2,3,5,6,}, R = {1,3,7,8,9}, S = {2,4,9,10}, then the number of elements in (PΔQ)Δ(RΔS) is
9) Answer: 7
Solution:
P = {1,2,3,4} and Q = {2,3,5,6,}
PΔQ = {1, 4, 5, 6}
R = {1,3,7,8,9} and S = {2,4,9,10}
RΔS = {1, 2, 3, 4, 7, 8, 10}
(PΔQ)Δ(RΔS) = {2, 3, 5, 6, 7, 8, 10}
Thus, there are 7 elements in (PΔQ)Δ(RΔS) .
hence, 7 is the correct answer.
Question 10: If A = {$6^{2n} -35n – 1$}, where $n$ = 1,2,3,… and B = {35($n$-1)}, where $n$ = 1,2,3,… then which of the following is true?
a) Every member of A is in B and at least one member of B is not in A
b) Neither every member of A is in B nor every member of B is in A
c) Every member of B is in A.
d) At least one member of A is not in B
10) Answer (A)
Solution:
If we carefully observe set A, then we find that $6^{2n} -35n – 1$ is divisible by 35. So, set A contains multiples of 35. However, not all the multiples of 35 are there in set A, for different values of $n$.
For $n = 1$, the value is 0, for $n = 2$, the value is 1225 which is the 35th multiple of 3.
If we observe set B, it consists of all the multiples of 35 including 0.
So, we can say that every member of set A will be in B while every member of set B will not necessarily be in set A.
Hence, option A is the correct answer.
Question 11: A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis is
a) 38
b) 32
c) 45
d) 43
11) Answer (D)
Solution:
Assume the number of members who can play exactly 1 game = I
The number of members who can play exactly 1 game = II
The number of members who can play exactly 1 game = III
I+2II+3III=144+123+132=399….(1)
I+II+III=256……(2)
=> II+2III=143…..(3)
Also, II+3III=58+25+63=146 ……(4)
=> III = 3 (From 3 and 4)
=> II =137
=> I = 116
The members who play only tennis = 123-58-25+3 = 43
Question 12: Students in a college have to choose at least two subjects from chemistry, mathematics and physics. The number of students choosing all three subjects is 18, choosing mathematics as one of their subjects is 23 and choosing physics as one of their subjects is 25. The smallest possible number of students who could choose chemistry as one of their subjects is
a) 22
b) 21
c) 20
d) 19
12) Answer (C)
Solution:
Now 23 students choose maths as one of their subject.
This means (MPC)+ (MC) + (PC)=23 where MPC denotes students who choose all the three subjects maths, physics and chemistry and so on.
So MC + PM =5 Similarly we have PC+ MP =7
We have to find the smallest number of students choosing chemistry
For that in the first equation let PM=5 and MC=0. In the second equation this PC=2
Hence minimum number of students choosing chemistry will be (18+2)=20 Since 18 students chose all the three subjects.
Question 13: In a certain town, 40% of people have brown hair, 30% of people have brown eyes and 12% have both brown hair and brown eyes.
How many people in town have neither brown hair nor brown eyes ?
a) 44%
b) 43%
c) 41%
d) 42%
13) Answer (D)
Solution:

Let total number of people in the town = $100x$
People who have both brown hair and eyes = $b=12x$
=> People who have brown hair = $a+b=40x$
=> $a=28x$
Similarly, $c=18x$
$\therefore$ People who have neither brown hair nor brown eyes = $100x-(12x+18x+28x)=42\%$
=> Ans – (D)
Question 14: For a set S, we denote by S’, the complement of the set S. Let X, Y, Z be Sets such that $Y \subseteq X$. Which of the following is always true?
a) $X \cap Z \subseteq Y \cap Z$
b) $Y’ \cap Z’ ⊇ X’ \cap Z’$
c) $X \cap (Y \cup Z) = Y \cup (X \cap Z)$
d) $X’ \cap Z ⊇ Y’ \cap Z$
14) Answer (B)
Solution:

Consider the above Diagram
For option A $X\cap Z$ = c+e and $Y\cap Z$ = e. Hence option A is False
For Option B $Y’\cap Z’$ = a+u and $X’\cap Z’$ = u. Option B is True
For Option C $X\cap\left(Y\cup Z\right)$ = c+d+e and $Y\cup\left(X\cap Z\right)$ = c+d+e. Option C is True
For option D $X’\cap Z$ = b and $Y’\cap Z$ = b+c. Option D is False
Question 15: Each student in a class of 40 plays at least one indoor game-chess, carom and scrabble. 18 play chess, 20 play scrabble and 27 play carom. 7 play both chess and scrabble, 12 play both scrabble and carom and 4 play all 3 games. The number of players who play chess and carom but not scrabble is
a) 10
b) 4
c) 6
d) 12
15) Answer (C)
Solution:
Students who play all the three games are 4, and with the rest information given in the question, we can at best draw the venn diagram as:

Now, total students=40.
So, Chess+ 5+8+15-x=40
=>18+28-x=40
=> 46-x=40
.’. x=6
Instructions
Read the information given below and answer the 2 associated questions.
190 students have to choose at least one elective and at most two electives from a list of three electives: E1, E2 and E3. It is found that the number of students choosing E1 is half the number of students choosing E2, and one third the number of students choosing E3.
Moreover, the number of students choosing two electives is 50.
Question 16: In addition to the given information, which of the following information is NECESSARY and SUFFICIENT to compute the number of students choosing only E1, only E2 and only E3?
a) Number of students choosing only E2, and number of students choosing both E2 and E3
b) Number of students choosing both E1 and E2, number of students choosing both E2 and E3, and number of students choosing both E3 and E1
c) Number of students choosing only E1, and number of students choosing both E2 and E3
d) No extra information is necessary
e) Number of students choosing both E1 and E2
16) Answer (A)
Solution:

Given, a+b+c=50 and a+b+c+x+y+z=190 => x+y+z=140.
Also, let E1=k => E2=2k and E3=3k
E1+E2+E3= 6k=190+50=240 => k=40.
Option A: If the number of students choosing only E2, the number of students
choosing both E2 and E3, are given then the number of students who choose E2 and E1, E1 and E3 can be found. From this only E1, only E3 can be calculated.
Option B: knowing the number of students choosing both E1 and E2, the number of students
choosing both E2 and E3, and a number of students choosing both E3 and E1 is insufficient. This information is not enough to calculate the number of students who choose only E1, only E2, and only E3.
Option C: If x and c are known, we can’t find y and z.
Option E is not sufficient.
Question 17: Which of the following CANNOT be obtained from the given information?
a) Number of students choosing E1
b) Number of students choosing either E1 or E2 or both, but not E3
c) Number of students choosing both E1 and E2
d) Number of students choosing E3
e) Number of students choosing exactly one elective
17) Answer (C)
Solution:

Given, a+b+c=50 and a+b+c+x+y+z=190 => x+y+z=140.
Also, let E1=k => E2=2k and E3=3k
E1+E2+E3= 6k=190+50=240 => k=40.
Option A, the number of students choosing E1 is 40.
Option B, number of students choosing either E1 or E2 or both, but not E3 = total – E3 = 190-120 = 70.
Option C, number of students choosing both E1 and E2 => this can not be obtained.
Option D, number of students choosing E3 = 3x = 120.
Option E, number of students choosing exactly one elective = Out of 190, 50 are choosing two electives, hence 190-50 = 140 are choosing exactly one elective.
Instructions
Answer the questions based on the information given below
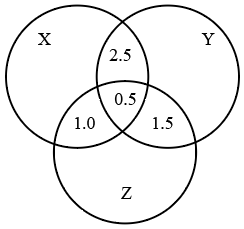
The Venn diagram given below shows the estimated readership of 3 daily newspapers (X, Y & Z) in a city. The total readership and advertising cost for each of these papers is as below
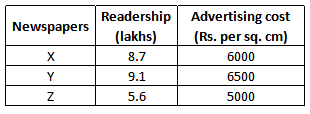
The total population of the city is estimated to be 14 million. The common readership (in lakhs) is indicated in the given Venn diagram
Question 18: The number of people (in lakhs) who read only one newspaper is
a) 4.7
b) 11.9
c) 17.4
d) 23.4
18) Answer (B)
Solution:
Given Readership of newspaper X = 8.7
only X + 2.5 + 0.5 + 1 = 8.7
only X = 4.7
Given Readership of newspaper Y = 9.1
only Y + 2.5 + 1.5 + 0.5 = 9.1
only Y = 4.6
Given Readership of newspaper Z = 5.6
only Z + 0.5 + 1 + 1.5 = 5.6
only Z = 2.6

Number of people who read only one newspaper = 4.7 + 4.6 + 2.6 = 11.9 lakhs
Question 19: A survey was conducted of 100 people whether they have read recent issues of ‘Golmal’, a monthly magazine. Summarized information is presented below :
Only September: 18
September but not August: 23
September and July: 8
September: 28
July: 48
July and August: 10
None of the three months: 24
What is the number of surveyed people who have read exactly for two consecutive months?
a) 7
b) 9
c) 12
d) 14
19) Answer (B)
Solution:
Exactly two consecutive months include both July-August and August-September. We cannot include July-September, as these months are not consecutive.

N – none of the three months
Number of people who read in July and August only = 7
Number of people who read in August and September only = 2
Therefore, the number of surveyed people who have read exactly for two consecutive months = 7+2 = 9
Answer is option B.
Question 20: During the placement season of a class, 21 students got shortlisted for company A, 26 got shortlisted for Company B and 29 got shortlisted for company C and 14 students got shortlisted for both A and B, 12 students got shortlisted for A and C and 15 for both B and C. All the companies shortlisted 8 students from the class. Then what is the ratio of number of students who got shortlisted for only B and number of students who got shortlisted for only C?
a) 1:1
b) 1:2
c) 2:3
d) 3:2
20) Answer (B)
Solution:

Given e = 8
Number of students shortlisted for A and B is 14
e + b = 14
b = 6
Number of students shortlisted for A and C is 12
e + d = 12
d = 4
Number of students shortlisted for B and C is 15
e + f = 15
f = 7
Given
Number of students shortlisted for B is 26
b + f + e + c = 26
6 + 7 + 8 + c = 26
c = 5
Number of students shortlisted for C is 29
d + e + f + g = 29
g = 10
Number of students shortlisted for A is 21
b + e + d + a = 21
a = 3

Number of students shortlisted for only B = c = 5
Number of students shortlisted for only C = g = 10
Ratio = 5:10 = 1:2
Answer is option B
Question 21: 400 students were admitted to the 2018-19 MBA batch. 200 of them did not choose “Business Statistics”. 100 of them did not choose “International Management’. There were 80 students who did not choose any of the two subjects. Find the number of students who chose both Business Statistics and International Management.
a) 180
b) 220
c) 280
d) 300
21) Answer (A)
Solution:
The number of students in 2018-19 MBA batch = 400
Number of students who did not choose ‘Business Statistics’ = 200
Number of students who did not choose ‘International Management’ = 100
Number of students who did not choose any of the two subjects = 80
Number of students who choose at least one of the two subjects = 400-80=320
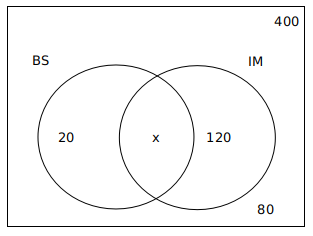
140+x=320
x=320-140=180
A is the correct answer.
Question 22: If A and B are two mutually exclusive and exhaustive events with $P(B) = 3P(A)$, then what is the value of $P(\overline{B})$?
a) $\frac{3}{4}$
b) $\frac{1}{4}$
c) $\frac{1}{3}$
d) $\frac{2}{3}$
22) Answer (B)
Solution:
Since P(B) and P(A) are mutually exclusive and exhaustive , thus, P(B)+P(A)=1
But we know that P(B)=3 P(A) , thus substituting in the above equation we get P(B)=3/4 and P(A)=1/4
Now they have asked P(B_) i.e. 1-P(B)=1-(3/4)=1/4
Question 23: In a school where there was a compulsion to learn at least one foreign language from the choice given to them, namely German, French and Spanish. Twenty eight students took French, thirty took German and thirty two took Spanish. Six students learnt French and
German, eight students learnt German and Spanish, ten students learnt French and Spanish. Fifty four students learnt only one foreign language while twenty students learnt only German. Find the number of students in the school.
a) 60
b) 62
c) 70
d) none of the above
23) Answer (C)
Solution:

Exactly 1 subject = a+b+c —> Represented by X
Exactly 2 subjects=d+e+f —–> Represented by Y
Exactly 3 subjects= g —–> Represented by Z
So X + Y+ Z + none = total ————–> (I)
German + French + Spanish = (a+b+c) +2(d+e+f) + 3(g) = X+ 2Y + 3Z ———–> (II)
So X+2Y+3Z= 30+28+32=90
Given X = 54
So 2Y +3Z = 36——–> (1)
Given ,
French and German = 6 => d+g = 6
German and Spanish = e+g = 8
French and Spanish = f + g = 10
adding all the three (d+e+f) + 3g = 24
Y + 3Z = 24 ——> (2)
solving 1 and 2 you get Y=12 and Z=4
Therefore Total = X+Y+Z+None = 54+12+4=70
Question 24: In a competitive exam there were 5 sections. 10% of the total number of students cleared the cut off in all the sections and 5% cleared none of the sections. From the remaining candidates 30% cleared only section 1, 20% cleared only section 2, 10% cleared only section 3 and remaining 1020 candidates cleared only section 4. How many students appeared in the competitive exam ?
a) 2550
b) 2800
c) 3000
d) 3200
24) Answer (C)
Solution:
Let total number of students=100x
10x=students who cleared the cut off in all the sections
5x=students who cleared none of the sections.
Remaining = 85x
Out of these 85x , 30% cleared only 1st section , 20% cleared only 2nd section, 30% cleared only section 3
Together they constitute 60% of 85x
Remaining= 40% of 85x =1020
On solving x=30
Total students=100x= 100*30=3000
Question 25: Of the 850 students who wrote an entrance examination at a center, 550 did very well in the Mathematics and Logical reasoning paper, 600 did very well in English language proficiency and 350 did very well in both. How many students did not do very well in Mathematics and Logical reasoning?
a) 300
b) 650
c) 50
d) 250
25) Answer (A)
Solution:
a= only maths
b=only logical reasoning
c= only English
d = only maths and logical reasoning
e= only maths and English
f= only Logical Reasoning and English
g= all three
a+b+c+d+e+f+g = 850
d+g = 550
c+e+f+g=600
d+e+f = 350
Question 26: Among a group of children, 6 children like only chocolate ice cream and 5 children like only butter scotch ice cream and 5 like either of the two. If each child gets an ice cream, how many ice creams should we order?
a) 11
b) 21
c) 16
d) 6
26) Answer (C)
Solution:
Children who like only chocolate ice cream = 6
Children who like only butter scotch ice cream = 5
Children who like both chocolate and butter scotch = 5
The given data can be represented in the Venn diagram as shown below

$\therefore\ $Total number of ice creams to be ordered = 6 + 5 + 5 = 16
Hence, the correct answer is Option C
Question 27: Among a group of 60 people who like Indian classical music, 38 like Hindustani music & 46 like Carnatic music. How many like both Hindustani & Carnatic?
a) 24
b) 84
c) 0
d) not possible to say as the required information is not given
27) Answer (A)
Solution:
Let a= only Carnatic music, b= only hindustani, c= both
a+b+c = 60
a+c = 46
b+c = 38
=> b=14
=> a=22
=> c= 24
Question 28: On a certain day when interviews for Master Degree courses were going on, it was found that 35 students attended interviews for MA Education, 47 students attended interviews for MSW and among the 2 groups, 12 students attended both. What is the total number of students who attended either of the interviews?
a) 82
b) 70
c) 94
d) 58
28) Answer (B)
Solution:
Let a = students who attended only MA
b= students who attended only MSW
c= students who attended both
a+c= 35
b+c = 47
c= 12
=> a=23 and b= 35
Total = a+b+c = 23 + 35 + 12 = 70
Question 29: There are 100 students in a class. in an examination, 50 of them failed in Mathematics, 45 failed in Physics and 40 failed in Biology. 32 failed in exactly two of the three subjects. Only one student passed in all the subjects. The number of students failing in all the three subjects is
a) 12
b) 4
c) 2
d) cannot be determined
29) Answer (C)
Solution:
Assume the number of students who failed in exactly 1 subject is x
The number of students who failed in exactly 2 subjects is y
The number of students who failed in exactly 3 subjects is z
Now, x+2y+3z=50+45+40=135
x+y+z=100-1=99
On subtracting the two equations, we get,
y+2z=36
It is given that y=32
Hence, 2z=36-32=4 =>z=2
Question 30: Let $P$ and $Q$ be two distinct nonempty sets. Then $(P \cup Q)^c \cup (P^c \cap Q)$ equals
a) $P^c$
b) $Q^c$
c) $P^c \cup Q^c$
d) $\phi$
30) Answer (A)
Solution:
$(P \cup Q)^c \cup (P^c \cap Q)$ = $\left(P^c\cap Q^c\right)\cup(P^c\cap Q)\ =\ P^c\cap\left(Q^cUQ\right)$
= $\ P^c\cap universal\ set$
= $\ P^c$
Question 31: If $P, Q, R$ are subsets of some universal set, then the conditions $P^c \cap Q \subseteq R^c \cap Q$ and $P^c \cap Q^c \subseteq R^c \cap Q^c$ imply
a) $R \subseteq P$
b) $P \subseteq R$
c) $Q = R$
d) $P = Q$
31) Answer (A)
Solution:
$P^c \cap Q \subseteq R^c \cap Q$
$P^c \cap Q^c \subseteq R^c \cap Q^c$
=> $\left(P^c\cap Q\right)U\ \left(P^c\cap Q^c\right)\subseteq\left(R^c\cap Q\right)U\ \left(R^c\cap Q^c\right)$
=> $P^c\cap\left(Q\ U\ Q^c\right)\subseteq R^c\cap\left(Q\ U\ Q^c\right)$
=> $P^c\subseteq R^c$
=>$R\subseteq P$
Question 32: In a survey conducted among 120 houses, it was found that 50 read Times of India, 60 read Indian Express and 48 read Hindustan Times; 20 read Times of India and Indian Express, 18 read Times of India and Hindustan Times and 24 read Indian Express and Hindustan Times. If 10 read all three, how many read only one
newspaper?
a) 50
b) 32
c) 64
d) 84
32) Answer (C)
Solution:

As can be seen from the above venn diagram distribution
Number of households reading only one newspaper = 22 + 26 + 16 = 64.
Hence, option C.
Question 33: In the final semester, an engineering college offers three elective courses and one mandatory course. A student has to register for exactly three courses: two electives and the mandatory course. The registration in three of the four courses is: 45, 55 and 70. What will be the number of students in the elective with the lowest registration?
a) 35
b) 40
c) 42
d) 45
e) Either B or D
33) Answer (E)
Solution:
The number of candidates registered for 3 of the 4 courses is 45, 55, and 70.
There are 2 cases.
70 can be the total number of students registered in an elective or the mandatory course.
Case (i):
70 students have registered in an elective.
Each student will choose 2 elective.
=> Total number of electives chosen = 2* total number of students.
45+55+70 = 2*number of students.
Number of students = 170/2 = 85.
In this case, at least 45 students would have selected an elective.
Case (ii):
70 students have registered in the mandatory class.
=> 45+55+x = 2*70
=> x =40.
As we can see, the number of students registered in an elective can be 40 or 45. Therefore, option E is the right answer.
Question 34: 70% of the students who joined XCRI last year play football, 75% play cricket, 80% play basketball and 85% play carrom. The minimum percentage of students who play all four games is:
a) 5%
b) 10%
c) 15%
d) 20%
e) None of the above
34) Answer (B)
Solution:
Let ‘100x’ be the number of students who joined XCRI last year.
Let ‘a’, ‘b’, ‘c’ and d be the number of students who play 1 game, 2 games, 3 games and 4 games respectively.
Therefore,
a+b+c+d = 100x … (1)
a+2b+3c+4d = 70x+75x+80x+85x
a+2b+3c+4d = 310x … (2)
By equation (2) – (1)
b+2c+3d = 210x
We have to minimize ‘d’ for that we have to maximize c. But c $\leq$ 100x
At c$_{max}$ = 90x, d$_{min}$ = 10x
Therefore, we can say that the minimum percentage of students who play all four games = 10%.
Question 35: In a class of 60, along with English as a common subject, students can opt to major in Mathematics, Physics, Biology or a combination of any two. 6 students major in both Mathematics and Physics, 15 major in both Physics and Biology, but no one majors in both Mathematics and Biology. In an English test, the average mark scored by students majoring in Mathematics is 45 and that of students majoring in Biology is 60. However, the combined average mark in English, of students of these two majors, is 50. What is the maximum possible number of students who major ONLY in Physics?
a) 30
b) 25
c) 20
d) 15
e) None of the above
35) Answer (D)
Solution:
Let us note down the information given:
No person can major in all 3 subjects. 6 students major in both Mathematics and Physics, 15 major in both Physics and Biology, but no one majors in both Mathematics and Biology. There are 60 students in total.

It has been given that average marks scored by students majoring in Maths in English is 45.
Average marks scored by students majoring in Biology in English is 60.
But the combined average marks scored by students majoring in Maths and Biology in English is 50.
=> $\dfrac{45*(a+6) + 60*(c+15)}{a+6+c+15} = 50$
$45a+270+60c+900 = 50a+50c+1050$
$5a=10c+120$
$a=2c+24$
To maximize b, we have to minimize ‘a’ and ‘c’. The least value that ‘c’ can take is 0.
The corresponding value of a is 24.
24+6+b+15 = 60
=> b = 15.
Therefore, the maximum number of students who could have majored only in physics is 15. Therefore,option D is the right answer.
Question 36: 290 students of MBA (International Business) in a reputed Business School have to study foreign language in Trimesters IV and V. Suppose the following information are given .
i. 120 students study Spanish
ii. 100 students study Mandarin
iii. At least 80 students, who study a foreign language, study neither Spanish nor Mandarin
Then the number of students who study Spanish but not Mandarin could be any number from
a) 80 to 170
b) 80 to 100
c) 50 to 80
d) 20 to 110
36) Answer (D)
Solution:

It’s given that 120 students study Spanish : A + B = 120 …(1)
Also 100 students study Mandarin : B + C = 100 …(2)
At least 80 students will not opt for any of these two languages i.e.
Spanish + Mandarin $\leq$ (290-80)
Spanish + Mandarin $\leq$ 210
A + B + C $\leq$ 210
Case 2: When B is minimum and A is maximum.
Solving for boundary condition A + B + C = 210 …(3)
Solving equations (1)+(2)-(3)
B = 10
i.e. A = 120 – B = 120 – 10 =110 {Maximum possible value of A}
Case 2: When B is maximum and A is minimum.
Since B+C = 100 so, Maximum value B can attain is 100. Hence, the minimum value of A = 120 – B = 120 – 100 = 20 {Minimum possible value of A}
So we can say that the number of students who study Spanish but not Mandarin will be A [20 ,110].
Question 37: In a certain village, 22% of the families own agricultural land, 18% own a mobile phone and 1600 families own both agricultural land and a mobile phone. If 68% of the families neither own agricultural land nor a mobile phone, then the total number of families living in the village is:
a) 20000
b) 10000
c) 8000
d) 5000
37) Answer (A)
Solution:
22% of the families own agricultural land, 18% own a mobile phone, 1600 families own both and 68% families own none.
P(A $\cup$ B) = P(A) + P(B) – P(A $\cap$ B)
32 = 22 + 18 – x
x=8. Hence, there will be 8% families who own both.
8% =1600 (Given in question)
Total families in a village =>100% = 20000
Question 38: There are 240 second year students in a B – School. The Finance area offers 3 electives in the second year. These are Financial Derivatives, Behavioural Finance, and Security Analysis. Four students have taken all the three electives, and 48 students have taken Financial Derivatives. There are twice as many students who study Financial Derivatives and Security Analysis but not Behavioural Finance, as those who study both Financial Derivatives and Behavioural Finance but not Security Analysis, and 4 times as many who study all the three. 124 students study Security Analysis. There are 59 students who could not muster courage to take up any of these subjects. The group of students who study both Financial Derivatives and Security Analysis but not Behavioural Finance, is exactly the same as the group made up of students who study both Behavioural Finance and Security Analysis. How many students study Behavioural Finance only?
a) 29
b) 30
c) 32
d) 35
e) None of the above
38) Answer (A)
Solution:

Given : $e = 4$
$FD = 48$, => $a + b + d + e = 48$
$d = 2b$ and $d = 4e$
$SA = 124$, => $d + e + f + g = 124$
$d = e + f$ and $h = 59$
To find : $c = ?$
Solution : $d = 4e = 4 \times 4 = 16$
=> $b = \frac{d}{2} = \frac{16}{2} = 8$
=> $f = d – e = 16 – 4 = 12$
=> $a = 48 – b – d – e = 48 – 8 – 16 – 4 = 20$
=> $g = 124 – d – e – f = 124 – 16 – 4 – 12 = 92$
Now, we know that, $a + b + c + d + e + f + g + h = 240$
=> $20 + 8 + c + 16 + 4 + 12 + 92 + 59 = 240$
=> $c + 211 = 240$
=> $c = 240 – 211 = 29$
Question 39: In a survey of political preference, 78% of those asked were in favor of at least one of the proposals: I, II and III. 50% of those asked favored proposal I, 30% favored proposal II, and 20% favored proposal III. If 5% of those asked favored all three of the proposals, what percentage of those asked favored more than one of the 3 proposals.
a) 10
b) 12
c) 17
d) 22
39) Answer (C)
Solution:
Let the distribution of votes for each of the proposal be as given below.
From the information given, we know that
a+b+c+d+e+f+g = 78 — (1)
a+b+e+f = 50 —- (2)
b+c+f+g = 30 —- (3)
e+f+g+d = 20 —- (4) and
f = 5 — (5)
We need to find b+e+g+f = ?
In the above equations, (2)+(3)+(4) – (1) implies
(a+b+e+f)+(b+c+f+g)+(e+f+g+d) – (a+b+c+d+e+f+g) = 50+30+20-78 = 22
Or, b+e+g+2f=22.
As, f = 5, it implies that b+e+g+f=17

Question 40: In a locality, two-thirds of the people have cable TV, one-fifth have VCR, and one-tenth have both. What is the fraction of people having atleast one among cable -TV and VCR?
a) $\frac{19}{30}$
b) $\frac{2}{3}$
c) $\frac{17}{30}$
d) $\frac{23}{30}$
40) Answer (D)
Solution:

Let the distribution of people having cable TV and VCR be as given in the diagram above.
Hence, $a+c =\frac{2}{3}$
$b+c=\frac{1}{5}$
and $c=\frac{1}{10}$
We need to find $a+b+c=?$
This equals $(a+b)+(b+c)-c = \frac{2}{3}+\frac{1}{5}-\frac{1}{10}$
Which equals $\frac{20+6-3}{30}=\frac{23}{30}$
So, these are some of the most important CAT Set Theory and Venn Diagram Questions. Practice these CAT Set Theory and Venn Diagram questions thoroughly. Learn all the major concepts from CAT set theory and Venn diagram questions. Also, do check out the Important CAT Set Theory and Venn Diagram questions & Formulas PDF here.




![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)
