CAT Percentage Questions [Important PDF]

Percentage Questions for CAT have appeared in the CAT Quant section. You can check out the CAT percentage questions based on CAT Previous year papers. In this article, we will look into some important percentage questions for CAT with solutions. These are a good source for practice; If you want to practice these questions, you can download these Percentage Questions for CAT PDF, which is completely Free.

Using this PDF one can understand the type of questions in percentage that can appear and can make practice more.

Click on the given below link to download the CAT percentage questions PDF with answers

Download Percentage Questions for CAT

Join CAT 2023 Online Coaching

Question 1: At the end of year 1998, Shepard bought nine dozen goats. Henceforth, every year he added p% of the goats at the beginning of the year and sold q% of the goats at the end of the year where p > 0 and q > 0. If Shepard had nine dozen goats at the end of year 2002, after making the sales for that year, which of the following is true?
[CAT 2003 leaked]

a) p = q

b) p < q

c) p > q

d) p = q/2

1) Answer (C)

View Video Solution

Solution:

By the end of the year 2002, Shepard bought 4 times and sold 4 times. He is left with the initial number of goats that he had in 1998. If the percentage of goats bought is equal to or lesser than the percentage of goats sold, then there would be a net decrease in the total number of goats. For the number of goats to remain the same, p has to be greater than q, because p% is being calculated in a lesser number and q% is being calculated on a greater number. Hence, p > q.

Question 2: The number of girls appearing for an admission test is twice the number of boys. If 30% of the girls and 45% of the boys get admission, the percentage of candidates who do not get admission is

a) 35

b) 50

c) 60

d) 65

2) Answer (D)

View Video Solution

Solution:

Let the number of girls be 2x and number of boys be x.

Girls getting admission = 0.6x

Boys getting admission = 0.45x

Number of students not getting admission = 3x – 0.6x -0.45x = 1.95x

Percentage = (1.95x/3x) * 100 = 65%

Question 3: In a village, the production of food grains increased by 40% and the per capita production of food grains increased by 27% during a certain period. The percentage by which the population of the village increased during the same period is nearest to

a) 16

b) 13

c) 10

d) 7

3) Answer (C)

View Video Solution

Solution:

Let initial population and production be x,y and final population be z
Final production = 1.4y, final percapita = 1.27 times initial percapita
=> $\frac{1.4y}{z} $ = $ 1.27 \times \frac{y}{x}$
=> $\frac{z}{x} = \frac{1.4}{1.27} \approx 1.10$
Hence the percentage increase in population = 10%

Question 4: A jar contains a mixture of 175 ml water and 700 ml alcohol. Gopal takes out 10% of the mixture and substitutes it by water of the same amount. The process is repeated once again. The percentage of water in the mixture is now

a) 30.3

b) 35.2

c) 25.4

d) 20.5

4) Answer (B)

View Video Solution

Solution:

Final quantity of alcohol in the mixture = $\dfrac{700}{700+175}*(\dfrac{90}{100})^2*[700+175]$ = 567 ml

Therefore, final quantity of water in the mixture = 875 – 567 = 308 ml

Hence, we can say that the percentage of water in the mixture = $\dfrac{308}{875}\times 100$ = 35.2 %

Question 5: The strength of a salt solution is p% if 100 ml of the solution contains p grams of salt. Each of three vessels A, B, C contains 500 ml of salt solution of strengths 10%, 22%, and 32%, respectively. Now, 100 ml of the solution in vessel A is transferred to vessel B. Then, 100 ml of the solution in vessel B is transferred to vessel C. Finally, 100 ml of the solution in vessel C is transferred to vessel A. The strength, in percentage, of the resulting solution in vessel A is

a) 15

b) 13

c) 12

d) 14

5) Answer (D)

View Video Solution

Solution:

Each of three vessels A, B, C contains 500 ml of salt solution of strengths 10%, 22%, and 32%, respectively.

The amount of salt in vessels A, B, C = 50 ml, 110 ml, 160 ml respectively.

The amount of water in vessels A, B, C = 450 ml, 390 ml, 340 ml respectively.

In 100 ml solution in vessel A, there will be 10ml of salt and 90 ml of water

Now, 100 ml of the solution in vessel A is transferred to vessel B. Then, 100 ml of the solution in vessel B is transferred to vessel C. Finally, 100 ml of the solution in vessel C is transferred to vessel A

i.e after the first transfer, the amount of salt in vessels A, B, C = 40, 120, 160 ml respectively.

after the second transfer, the amount of salt in vessels A, B, C =40, 100, 180 ml respectively.

After the third transfer, the amount of salt in vessels A, B, C = 70, 100, 150 respectively.

Each transfer can be captured through the following table.

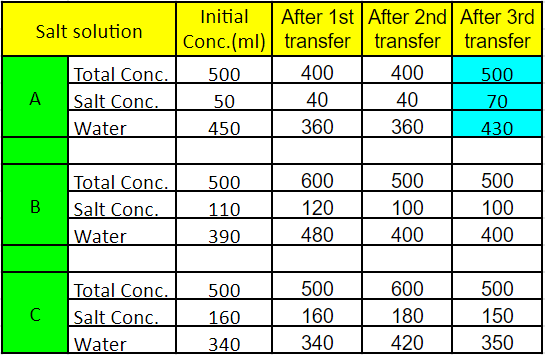
Percentage of salt in vessel A =$\ \frac{\ 70}{500}\times\ 100$

=14%

Question 6: The salaries of Ramesh, Ganesh and Rajesh were in the ratio 6:5:7 in 2010, and in the ratio 3:4:3 in 2015. If Ramesh’s salary increased by 25% during 2010-2015, then the percentage increase in Rajesh’s salary during this period is closest to

a) 10

b) 7

c) 9

d) 8

6) Answer (B)

View Video Solution

Solution:

Let the salaries of Ramesh, Ganesh and Rajesh in 2010 be 6x, 5x, 7x respectively

Let the salaries of Ramesh, Ganesh and Rajesh in 2015 be 3y, 4y, 3y respectively

It is given that Ramesh’s salary increased by 25% during 2010-2015,3y = 1.25*6x

y=2.5x

Percentage increase in Rajesh’s salary = 7.5-7/7=0.07

=7%

Question 7: In a class, 60% of the students are girls and the rest are boys. There are 30 more girls than boys. If 68% of the students, including 30 boys, pass an examination, the percentage of the girls who do not pass is

7) Answer: 20

View Video Solution

Solution:

Assuming the number of students =100x

Hence, the number of girls = 60x and the number of boys = 40x

We have, 60x-40x=30  => x=1.5

The number of girls = 60*1.5=90

Number of girls that pass = 68x-30=68*1.5-30 = 102-30=72

The number of girls who do not pass = 90-72=18

Hence the percentage of girls who do not pass = 1800/90=20

Question 8: A chemist mixes two liquids 1 and 2. One litre of liquid 1 weighs 1 kg and one litre of liquid 2 weighs 800 gm. If half litre of the mixture weighs 480 gm, then the percentage of liquid 1 in the mixture, in terms of volume, is

a) 80

b) 70

c) 85

d) 75

8) Answer (A)

View Video Solution

Solution:

The weight/volume(g/L) for liquid 1 = 1000

The weight/volume(g/L) for liquid 2 = 800

The weight/volume(g/L) of the mixture = 480/(1/2) = 960

Using alligation the ratio of liquid 1 and liquid 2 in the mixture = (960-800)/(1000-960) = 160/40 = 4:1

Hence the percentage of liquid 1 in the mixture = 4*100/(4+1)=80

Question 9: Two alcohol solutions, A and B, are mixed in the proportion 1:3 by volume. The volume of the mixture is then doubled by adding solution A such that the resulting mixture has 72% alcohol. If solution A has 60% alcohol, then the percentage of alcohol in solution B is

a) 90%

b) 94%

c) 92%

d) 89%

9) Answer (C)

View Video Solution

Solution:

Initially let’s consider A and B as one component

The volume of the mixture is doubled by adding A(60% alcohol) i.e they are mixed in 1:1 ratio and the resultant mixture has 72% alcohol.

Let the percentage of alcohol in component 1 be ‘x’.

Using allegations , $\frac{\left(72-60\right)}{x-72}=\frac{1}{1}$ => x= 84

Percentage of alcohol in A = 60% => Let’s percentage of alcohol in B = x%

The resultant mixture has 84% alcohol. ratio = 1:3

Using allegations , $\frac{\left(x-84\right)}{84-60}=\frac{1}{3}$

=> x= 92%

Question 10: The strength of an indigo solution in percentage is equal to the amount of indigo in grams per 100 cc of water. Two 800 cc bottles are filled with indigo solutions of strengths 33% and 17%, respectively. A part of the solution from the first bottle is thrown away and replaced by an equal volume of the solution from the second bottle. If the strength of the indigo solution in the first bottle has now changed to 21% then the volume, in cc, of the solution left in the second bottle is

10) Answer: 200

View Video Solution

Solution:

Let Bottle A have an indigo solution of strength 33% while Bottle B have an indigo solution of strength 17%.

The ratio in which we mix these two solutions to obtain a resultant solution of strength 21% : $\frac{A}{B}=\frac{21-17}{33-21}=\frac{4}{12}or\ \frac{1}{3}$

Hence, three parts of the solution from Bottle B is mixed with one part of the solution from Bottle A. For this process to happen, we need to displace 600 cc of solution from Bottle A and replace it with 600 cc of solution from Bottle B {since both bottles have 800 cc, three parts of this volume = 600cc}.As a result, 200 cc of the solution remains in Bottle B.

Hence, the correct answer is 200 cc.

Question 11: Identical chocolate pieces are sold in boxes of two sizes, small and large. The large box is sold for twice the price of the small box. If the selling price per gram of chocolate in the large box is 12% less than that in the small box, then the percentage by which the weight of chocolate in the large box exceeds that in the small box is nearest to

a) 144

b) 127

c) 135

d) 124

11) Answer (B)

View Video Solution

Solution:

Let the selling price of the Large and Small boxes of chocolates be Rs.200 and Rs.100 respectively. Let us consider that the Large box has $L$ grams of chocolate while the Small box has $S$ grams of chocolate.

The relation between the selling price per gram of chocolate can be represented as: $\frac{200}{L}=0.88\times\ \frac{100}{S}$

On solving we obtain the ratio of the amount of chocolate in each box as: $\frac{L}{S}=\frac{25}{11}$

The percentage by which the weight of chocolate in the large box exceeds that in the small box = $\left(\frac{25}{11}-1\right)\times\ 100\approx\ 127\%$

Question 12: In a tournament, a team has played 40 matches so far and won 30% of them. If they win 60% of the remaining matches, their overall win percentage will be 50%. Suppose they win 90% of the remaining matches, then the total number of matches won by the team in the tournament will be

a) 80

b) 78

c) 84

d) 86

12) Answer (C)

View Video Solution

Solution:

Initially number of matches = 40
Now matches won = 12
Now let remaining matches be x
Now number of matches won = 0.6x
Now as per the condition :
$\frac{\left(12+0.6x\right)}{40+x}=\frac{1}{2}$
24 +1.2x=40+x
0.2x=16
x=80
Now when they won 90% of remaining = 80(0.9) =72
So total won = 84

Question 13: The total of male and female populations in a city increased by 25% from 1970 to 1980. During the same period, the male population increased by 40% while the female population increased by 20%. From 1980 to 1990, the female population increased by 25%. In 1990, if the female population is twice the male population, then the percentage increase in the total of male and female populations in the city from 1970 to 1990 is

a) 68.25

b) 68.75

c) 68.50

d) 69.25

13) Answer (B)

View Video Solution

Solution:

Let us solve this question by assuming values(multiples of 100) and not variables(x).

Since we know that the female population was twice the male population in 1990, let us assume their respective values as 200 and 100.

Note that while assuming numbers, some of the population values might come out as a fraction(which is not possible, since the population needs to be a natural number). However, this would not affect our answer, since the calculations are in ratios and percentages and not real values of the population in any given year.

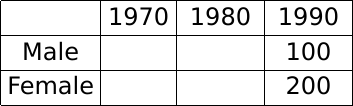
Now, we know that the female population became 1.25 times itself in 1990 from what it was in 1980.

Hence, the female population in 1980 = 200/1.25 = 160

Also, the female population became 1.2 times itself in 1980 from what it was in 1970.

Hence, the female population in 1970 = 160/1.2 = 1600/12 = 400/3

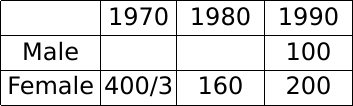
Let the male population in 1970 be x. Hence, the male population in 1980 is 1.4x.

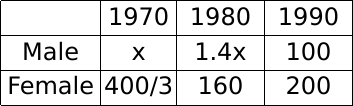
Now, the total population in 1980 = 1.25 times the total population in 1970.

Hence, 1.25 (x + 400/3) = 1.4x + 160

Hence, x = 400/9.

Population change = 300 – 400/9 – 400/3 = 300 – 1600/9 = 1100/9

percentage change = $\frac{\frac{1100}{9}}{\frac{1600}{9}}\times\ 100\ =\ \frac{1100}{16}\%=68.75\%$

Download CAT 2023 Study Plan PDF