CAT Questions On Lines And Angles PDF:
Download CAT Questions On Lines And Angles PDF. Practice important problems on CAT geometry Questions On Lines And Angles with detailed explanations and solutions.
Download CAT Questions On Lines And Angles PDF
Download All Quantitative Aptitude important Questions PDF
Take Free Mock Test for CAT 2018
Question 1: In a triangle ABC, Angle B = 60 degres and Angle C = 45 degrees. D is a point on BC such that AD divides BC in the ratio 1:4. Find the value of $\left \lfloor \frac{sin(BAD)}{sin(CAD)} \right \rfloor$.$\left \lfloor \ \right \rfloor$ refers to the greatest integer function less than or equal to x.
a) 1
b) 0
c) 3
d) 5
Question 2: A regular polygon P has 135 diagonals. Find the exterior angle of the polygon P.
a) $18^{\circ}$
b) $20^{\circ}$
c) $25^{\circ}$
d) $30^{\circ}$
Question 3: A circle touches all the three sides of the triangle as shown in the given figure at points P, Q and R respectively. If Angle RPQ is 50 degrees, find the measure of angle BAC (in degrees)?
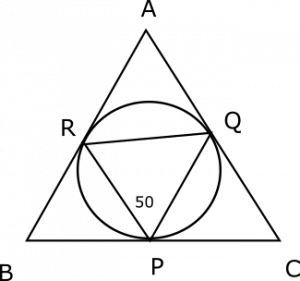
a) 65
b) 70
c) 80
d) 96
Question 4: Tangents are drawn from the points (6,8) to the circle $x^2+y^2=36$. Find the angle between the two tangents approximately.
a) $64^{\circ}$
b) $74^{\circ}$
c) $84^{\circ}$
d) $94^{\circ}$
Question 5: A square ABCD has a side of length 3cm. A point E on CD divides CD in such a way that CE:ED = 1:2. AC and BE intersect at P. Find cos(Angle EPC).
a) $\frac{1}{\sqrt{20}}$
b) $\frac{1}{\sqrt{10}}$
c) $\frac{2}{\sqrt{10}}$
d) $\frac{1}{\sqrt{5}}$
CAT Mocks for just Rs. 1180 – Last Day
Answers & Solutions:
1) Answer (B)
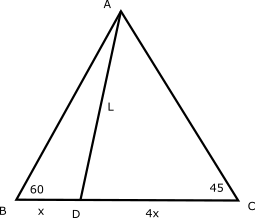
In triangle ABD,
$\frac{sin(BAD)}{x} =\frac{sin 60}{L}$
In triangle CAD,
$\frac{sin(CAD)}{4x} =\frac{sin 45}{L}$
$4\frac{sin(BAD)}{sin(CAD)} = \frac{\sqrt{3}}{\sqrt{2}} = 1.22$
=> $\frac{sin(BAD)}{sin(CAD)} = 1.22/4 = .305$
$\left \lfloor \frac{sin(BAD)}{sin(CAD)} \right \rfloor$ = $\left \lfloor .305 \right \rfloor$ = 0
2) Answer (B)
Number of diagonals in a regular polygon = $^nC_2 – n$
=> $^nC_2 – n$ = 135
=> n = 18
Exterior angle = $\frac{360}{n}$ = $\frac{360}{18}$ = $20^{\circ}$
3) Answer (C)
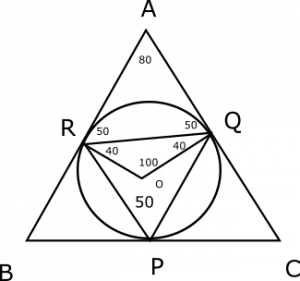
Angle = ROQ = 2*50 = 100 degrees
Since OR = OQ
Angle ORQ = Angle OQR = (180-100)/2 = 40 degrees
Since line drawn from the centre to the point of contact is perpendicular to the tangent,
Angle ARQ = Angle AQR = 90-40 = 50 degrees
Angle RAQ = 180-50-50 = 80 degrees
4) Answer (B)
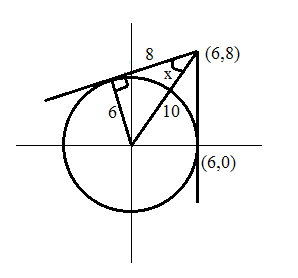
Let the angle between the tangents be 2x.
The radius of the circle is 6 and the center is (0,0).
=> Distance betweenthe center and point (6,8) is $\sqrt{6^2+8^2}$ = 10
=> Length of the tangent = $\sqrt{10^2-6^2}$ = 8
$\sin x$ = 6/10 = 0.6
$\sin 30^{\circ}$ = 0.5 and $\sin 45^{\circ}$ = $\frac{1}{\sqrt{2}}$ = 0.7
=> x must be around $35^{\circ}$ to $38^{\circ}$
=> 2x must be around $70^{\circ}$ to $76^{\circ}$
Among the options, option B is the closest answer.
5) Answer (D)
The diagram is as shown below.
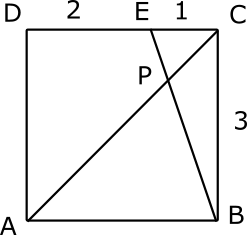
Angle PCE = 45 degrees
Angle PEC =$cos^{-1}$(1/$\sqrt{10}$)
Angle EPC = 180-45-$cos^{-1}$(1/$\sqrt{10}$) = 135-$cos^{-1}$(1/$\sqrt{10}$)
cos(Angle EPC) = cos(135-$cos^{-1}$(1/$\sqrt{10})$ ) = cos(135)cos($cos^{-1}$(1/$\sqrt{10}$))+sin135sin($cos^{-1}$(1/$\sqrt{10})$)
cos(Angle EPC) = -$1/\sqrt{20}$+$3/\sqrt{20}$ = $\frac{1}{\sqrt{5}}$
