CAT Questions On Cubes:
Download CAT important Questions on Cubes PDF. Previous CAT exam asked questions on Cubes theory. General Cube theory questions will be asked in logical reasoning for CAT.
Read very important Cubes theory for CAT
Download CAT Questions On Cubes
Download LR Puzzles Set-1 PDF
Download All CAT LR Questions PDF
Question 1: A cube of side length 8 cm is taken and small cubes of 2 cm length are cut along all the eight corners of the cube. By what percentage does the total surface area of the cube changes?
a) 5%
b) 12.5%
c) 20%
d) None of these
Question 2: A cuboid of dimensions 45cm, 75cm and 90cm is to be divided into identical cubes of side X cm. What is the maximum possible value of X?
a) 10
b) 12
c) 15
d) 17
Question 3: Four cubes are placed adjacently in a row. What is the ratio of the surface area of the new cuboid to the total surface area of the four cubes?
a) 9/16
b) 3/4
c) 16/9
d) 4/3
Question 4: A cube of side 3 cm is cut into smaller cubes of side 1 cm. What is the ratio of Total surface area of the larger cube and the sum of the total surfaces of all the smaller cubes?
a) 1:1
b) 1:2
c) 1:3
d) 1:4
Question 5: A cube of side n is painted green on all its sides. It is then cut into $n^3$ identical cubes. How many of the smaller cubes will have three of its sides painted?
a) 4
b) 6
c) 8
d) cannot be determined
Factors of a number – Formulas for CAT
Formulas on Number system and factorials
Answers & Solutions:
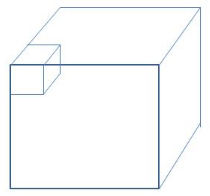
1) Answer (D)
Each cube that is cut had three sides exposed outside and three sides not exposed when it was in the bigger cube.
2) Answer (C)
As it is given that the smaller cubes to be formed are to be identical and for the side of it to be maximum it has to be the HCF of the dimensions of the given cuboid.
HCF of 45, 75 and 90 is 15.
Hence the maximum possible value of the side of the smaller cubes is 15.
3) Answer (B)
Let a be the side of the small cuboid. Surface area of one cuboid = 6$a^2$
Thus, the total surface area of the 4 cubes = 4 x 6$a^2$ = 24$a^2$
The side of the new cuboid formed is a, a and 4a. The total surface area of the new cuboid formed = 2($a^2 + 4a^2 + 4a^2 ) =18a^2$
Thus, the surface area of the new cuboid to that of the 4 cubes = $18a^2/24a^2$ = 3/4
4) Answer (C)
Total surface area of the larger cube = 6*3*3 = 54.
Total surface area of a smaller cube = 6*1*1 = 6.
The number of smaller cubes = 3*3*3 = 27.
Sum of the total surface areas of all the smaller cubes = 6*27 = 162.
Thus the required ratio = 54:162 = 1:3.
5) Answer (C)
Since, all the sides of the cube is painted, the cubes cut out from the corners will have three of its faces green. Since there are 8 corners for a cube, there will be 8 such cubes.
CAT Online Most Trusted Courses




![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)
