CAT Geometry Questions PDF [Important]
Geometry is one of the key topics in the CAT Quant Section. If you’re not very strong in this topic, it is essential that you know the basics of CAT Geometry. Also, do check out all the Geometry questions from the CAT Previous Papers with detailed video solutions. This article will look into some important Geometry questions for the CAT Exam. If you want to practice these important Geometry questions for CAT, you can download the PDF, which is completely Free.
Download Geometry Questions for CAT
Enroll for CAT 2022 Crash Course
Question 1: Let ABCD be a parallelogram. The lengths of the side AD and the diogonal AC are 10cm and 20cm, respectively. If the angle $\angle ADC$ is equal to $30^{0}$ then the area of the parallelogram, in sq.cm is
a) $\frac{25(\sqrt{5}+\sqrt{15})}{2}$
b) $25(\sqrt{3}+\sqrt{15})$
c) $\frac{25(\sqrt{3}+\sqrt{15})}{2}$
d) ${25(\sqrt{5}+\sqrt{15})}$
1) Answer (B)
Solution:
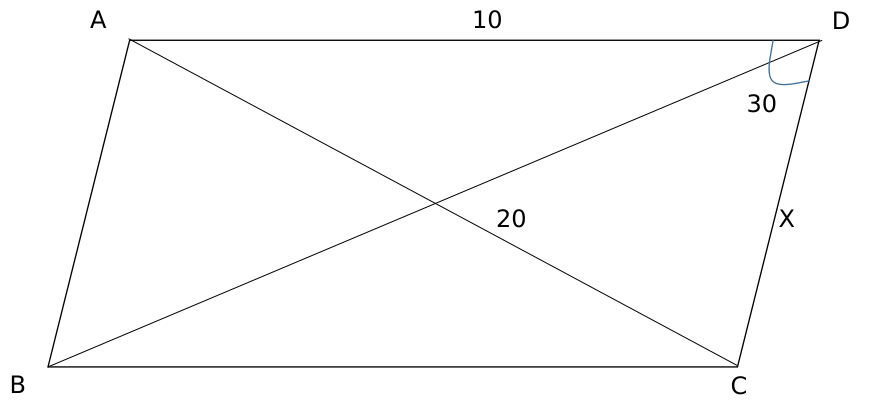
Applying cosine rule in triangle ACD,
$100+X^2-2\times\ 10\times\ X\cos30=400$
$X^2-10X\sqrt{\ 3}-300=0$
Solving, we get X = $\left(\frac{10\sqrt{\ 3}+10\sqrt{\ 15}}{2}\right)$
Hence, area = 10Xsin 30 = $\frac{\left(\frac{10\sqrt{\ 3}+10\sqrt{\ 15}}{2}\right)10}{2}$
= $25(\sqrt{3}+\sqrt{15})$
Question 2: If a triangle ABC, $\angle BCA=50^{0}$. D and E are points on $AB$ and $AC$, respectively, such that $AD=DE$. If F is a point on $BC$ such that $BD=DF$, then $\angle FDE$, in degrees, is equal to
a) 72
b) 80
c) 100
d) 96
2) Answer (B)
Solution:
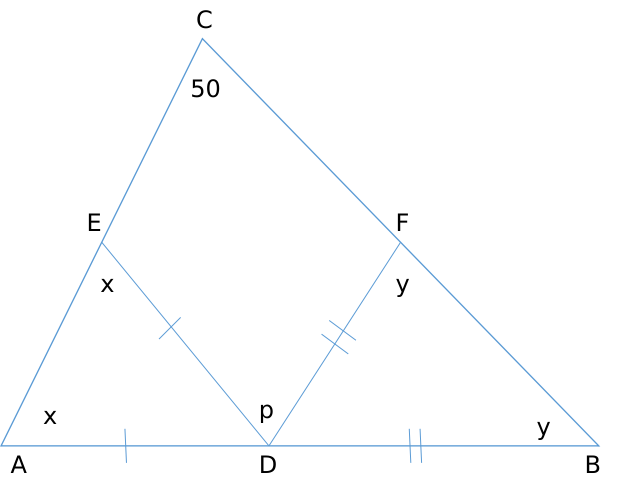
We need to find out p.
Angle ADE = 180 – 2x
Angle BDF = 180 – 2y
Now, 180 – 2y + p + 180 – 2x = 180 [Straight line = 180 deg]
p = 2x + 2y – 180
Also, x + y + 50 = 180 [Sum of the angles of triangle = 180]
x + y = 130
p = 260 – 180 = 80 degrees.
Question 3: A park is shaped like a rhombus and has area 96 sq m. If 40 m of fencing is needed to enclose the park, the cost, in INR, of laying electric wires along its two diagonals, at the rate of ₹125 per m, is
3) Answer: 3500
Solution:
We can say 40m is the perimeter of the park
so side of rhombus = 10
Now $\frac{1}{2}\times\ d_1\times\ d_2\ =\ 96$
so we get $\ d_1\times\ d_2\ =\ 192$ (1)
And as we know diagonals of a rhombus are perpendicular bisectors of each other :
so $\ \frac{d_1^2}{4}+\ \frac{d_2^2}{4}=\ 100$
so we get $\ d_1^2+\ d_2^2=\ 400$ (2)
Solving (1) and (2)
We get $d_1=12$ and$d_2=16$
Now the cost, in INR, of laying electric wires along its two diagonals, at the rate of ₹125 per m, is= (12+16)(125) =3500
Question 4: The cost of fencing a rectangular plot is ₹ 200 per ft along one side, and ₹ 100 per ft along the three other sides. If the area of the rectangular plot is 60000 sq. ft, then the lowest possible cost of fencing all four sides, in INR, is
a) 120000
b) 90000
c) 100000
d) 160000
4) Answer (A)
Solution:
Let us draw the rectangle.

Now, definitely, three sides should be fenced at Rs 100/ft, and one side should be fenced at Rs 200/ft.
In this question, we are going to assume that the L is greater than B.
Hence, the one side painted at Rs 200/ft should be B to minimise costs.
Hence, the total cost = 200B + 100B + 100L + 100L = 300B + 200L
Now, L x B = 60000
B = 60000/L
Hence, total cost = 300B + 200L = 18000000/L + 200L
To minimise this cost, we can use AM>=GM,
$\frac{\frac{18000000}{L}+200L}{2}\ge\sqrt{\ \frac{18000000}{L}\times\ 200L}$
$\frac{18000000}{L}+200L\ge2\sqrt{\ 18000000\times\ 200}$
$\frac{18000000}{L}+200L\ge2\times\ 60000$
Hence, minimum cost = Rs 120000.
Question 5: Let D and E be points on sides AB and AC, respectively, of a triangle ABC, such that AD : BD = 2 : 1 and AE : CE = 2 : 3. If the area of the triangle ADE is 8 sq cm, then the area of the triangle ABC, in sq cm, is
5) Answer: 30
Solution:
We have :
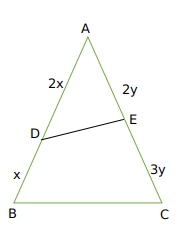
Now area of ADE = $\frac{1}{2}\times\ AD\times\ AE\times\ \sin A$
=$\frac{1}{2}\times\ 2x\times\ 2y\times\ \sin A=8$
we get xy sinA =4
Now Area of triangle ABC = $\frac{1}{2}AB\times\ AC\times\ \sin A$
we get $\frac{1}{2}\times3x\ \times5y\ \sin A=\frac{15}{2}xy\ \sin A=\ \frac{15}{2}\times\ 4$
we get Area of ABC = 30
Checkout: CAT Free Practice Questions and Videos
Question 6: The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is
a) 30
b) 40
c) 25
d) 20
6) Answer (A)
Solution:
We are given that :
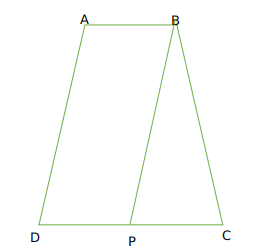
Let DP =x
So AB =x
Now DP=CP
So CD = 2x
Now let height of trapezium be h
we can say A(Parallelogram ABPD ) = xh
And A (BPC) =$\frac{1}{2}xh$
Now by condition$xh-\frac{1}{2}xh=10$
$\frac{xh}{2}=10$
so xh =20
Now therefore area of trapezium ABCD = $\frac{1}{2}\left(x+2x\right)h\ =\ \frac{3}{2}xh\ =\ 30$
Question 7: If a rhombus has area 12 sq cm and side length 5 cm, then the length, in cm, of its longer diagonal is
a) $\sqrt{37}+\sqrt{13}$
b) $\sqrt{13}+\sqrt{12}$
c) $\frac{\sqrt{37}+\sqrt{13}}{2}$
d) $\frac{\sqrt{13}+\sqrt{12}}{2}$
7) Answer (A)
Solution:
All the sides of the rhombus are equal.
The area of a rhombus is $12\ cm^2$
Considering d1 to be the length of the longer diagonal, d2 to be the length of the shorter diagonal.
The area of a rhombus is $\left(\frac{1}{2}\right)\left(d1\right)\cdot\left(d2\right)\ =\ 12$
d1*d2 = 24.
The length of the side of a rhombus is given by $\frac{\sqrt{\ d1^2+d2^2}}{2}$. This is because the two diagonals and a side from a right-angled triangle with sides d1/2, d2/2 and the side length.
$\frac{\sqrt{\ d1^2+d2^2}}{2}=\ 5$
Hence $\sqrt{\ d1^2+d2^2}\ =\ 10$
$d1^2+d2^2\ =\ 100$
Using d1*d2 = 24, 2*d1*d2 = 48.
$d1^2+d2^2\ +2\cdot d1\cdot d2=\ 100+48\ =\ 148$
$d1^2+d2^2\ -2\cdot d1\cdot d2=\ 100-48\ =\ 52$
$d1+d2\ =\ \sqrt{\ 148}$ (1)
d1-d2 = $\sqrt{52}$ (2)
(1) + (2)= 2*(d1) = 2*($\sqrt{\ 37}+\sqrt{\ 13}$)
d1 = $\sqrt{\ 37}+\sqrt{\ 13}$
or
In a rhombus the area of a Rhombus is given by :
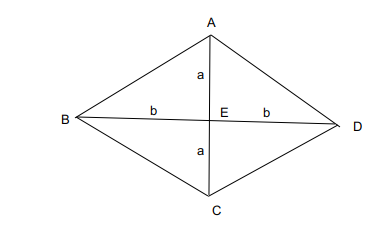
The diagonals perpendicularly bisect each other. Considering the length of the diagonal to be 2a, 2b.
The area of a Rhombus is : $\left(\frac{1}{2}\right)\cdot\left(2a\right)\cdot\left(2b\right)\ =\ 12$
ab =6.
The length of each side is : $\sqrt{\ a^2+b^2}$ = 5, $a^2+b^{2\ }=\ 25,\ $
$\left(a+b\right)^2=\ 37,\ \left(a+b\right)\ =\ \sqrt{\ 37}$
($\left(a-b\right)^2=\ 13,\ a-b\ =\ \sqrt{\ 13}$
$2a\ =\ \left(\sqrt{\ 37}+\sqrt{\ 13}\right)$, $2b\ =\ \left(\sqrt{\ 37}-\sqrt{\ 13}\right)$.
2a is longer diagonal which is equal to $\ \left(\sqrt{\ 37}+\sqrt{\ 13}\right)$
Question 8: A circle of diameter 8 inches is inscribed in a triangle ABC where $\angle ABC = 90^\circ$. If BC = 10 inches then the area of the triangle in square inches is
8) Answer: 120
Solution:
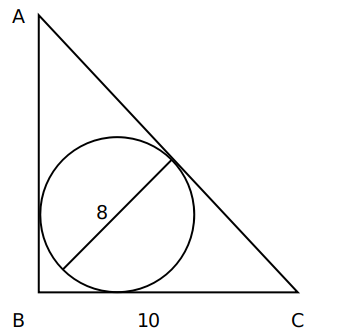
We know that Inradius=$\frac{\left(Perpendicular+Base-Hypotenuse\right)}{2}$
$4=\frac{\left(p+10-h\right)}{2}$
h-p = 2 or h= p+2.
Now, $p^2+100\ =\ h^2$
$p^2+100\ =\ \left(p+2\right)^2$
$p^2+100\ =\ p^2+4p+4$
4p = 96
p=24.
Hence, Area = $\frac{1}{2}\times\ 10\times\ 24\ =\ 120$.
Question 9: Suppose the length of each side of a regular hexagon ABCDEF is 2 cm.It T is the mid point of CD,then the length of AT, in cm, is
a) $\sqrt{13}$
b) $\sqrt{14}$
c) $\sqrt{12}$
d) $\sqrt{15}$
9) Answer (A)
Solution:
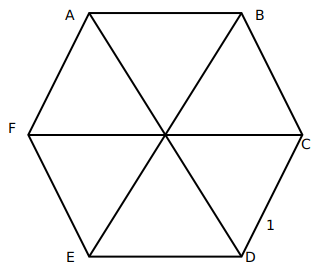
Since a regular hexagon can be considered to be made up of 6 equilateral triangles, a line joining the farthest vertices of a hexagon can be considered to be made up using the sides of two opposite equilateral triangle forming the hexagon. Hence, its length should be twice the side of the hexagon, in this case, 4 cm.
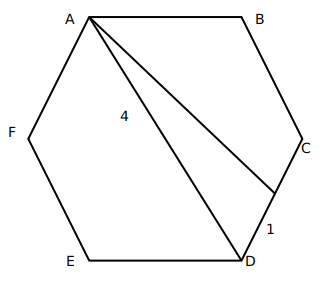
Now, AD divided the hexagon into two symmetrical halves. Hence, AD bisects angle D, and hence, angle ADC is $60^{\circ\ }$.
We can find out the value of AT using cosine formula:
$AT^2=\ 4^2+1^2-2\times\ 1\times\ 4\cos60$
$AT^2=\ 17-4=13$
$AT=\sqrt{\ 13}$
Question 10: If the area of a regular hexagon is equal to the area of an equilateral triangle of side 12 cm, then the length, in cm, of each side of the hexagon is
a) $4\sqrt{6}$
b) $6\sqrt{6}$
c) $\sqrt{6}$
d) $2\sqrt{6}$
10) Answer (D)
Solution:
Area of a regular hexagon = $\frac{3\sqrt{3}}{2}x^2$
Area of an equilateral triangle = $\frac{\sqrt{3}}{4}\left(a\right)^2$ ; where a = side of the triangle
Since the area of the two figures are equal, we can equate them as folllows: $\frac{3\sqrt{3}}{2}x^2=\frac{\sqrt{3}}{4}\left(12\right)^2$
On simplifying: $x^2=24\ $
$\therefore\ x=2\sqrt{6}$




![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)
