Download Games and Tournaments Questions for CAT

Get CAT 2023 Mocks At Rs. 499

Instructions

Answer the following questions based on the information given below:

In a sports event, six teams (A, B, C, D, E and F) are competing against each other Matches are scheduled in two stages. Each team plays three matches in Stage – I and two matches in Stage – II. No team plays against the same team more than once in the event. No ties are permitted in any of the matches. The observations after the completion of Stage – I and Stage – II are as given below.

Stage-I:

• One team won all the three matches.

• Two teams lost all the matches.

• D lost to A but won against C and F.

• E lost to B but won against C and F.

• B lost at least one match.

• F did not play against the top team of Stage-I.

Stage-II:

• The leader of Stage-I lost the next two matches

• Of the two teams at the bottom after Stage-I, one team won both matches, while the other lost both matches.

• One more team lost both matches in Stage-II.

Question 1: The two teams that defeated the leader of Stage-I are:

a) B & F

b) E & F

c) B & D

d) E & D

e) F & D

1) Answer (B)

View Video Solution

Solution:

There are a total of $^6 C_2$ matches => 15 matches. The first 9 matches are held in the first stage and remaining 6 in the second stage.

From the information given, we can conclude that the following matches were held in first stage:

Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won)

One team won all matches. As B, C, D E and F have lost at least one match each, A won all three matches. As A, B, D, E have won at least one match, C and F lost both matches.

From the matches already deduced, we can see that A needs to play 2 more matches, B two more matches and C and F one match each. As C and F lose all matches in stage 1, they cannot play against each other. F did not play against the leader i.e. A. Hence, the remaining matches are A-B (A won), A-C (A won), B-F (B won).

Thus, the stage 1 matches are

Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won), A-B (A won), A-C (A won), B-F (B won)

Thus Stage 2 matches are D-B, D-E, E-A, F-A, B-C and C-F (all matches – stage 1 matches)

As A lost both matches, F and E must have won the match vs A. As F won against A, F won both its matches and C lost both its matches. One more team lost both its matches. As B, E and F have won at least one match and A and C have been discussed previously, D must have lost both matches. Hence, stage 2 results are:

Stage 2: D-B (B won), D-E (E won), E-A (E won), F-A (F won), B-C (B won) and C-F (F won)

Hence, the two teams that won against stage 1 leader A are E and F.

Question 2: The only team(s) that won both matches in Stage-II is (are):

a) B

b) E & F

c) A, E & F

d) B, E & F

e) B & F

2) Answer (D)

View Video Solution

Solution:

There are a total of $^6 C_2$ matches => 15 matches. The first 9 matches are held in the first stage and remaining 6 in the second stage.

From the information given, we can conclude that the following matches were held in first stage:

Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won)

One team won all matches. As B, C, D E and F have lost at least one match each, A won all three matches. As A, B, D, E have won at least one match, C and F lost both matches.

From the matches already deduced, we can see that A needs to play 2 more matches, B two more matches and C and F one match each. As C and F lose all matches in stage 1, they cannot play against each other. F did not play against the leader i.e. A. Hence, the remaining matches are A-B (A won), A-C (A won), B-F (B won).

Thus, the stage 1 matches are

Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won), A-B (A won), A-C (A won), B-F (B won)

Thus Stage 2 matches are D-B, D-E, E-A, F-A, B-C and C-F (all matches – stage 1 matches)

As A lost both matches, F and E must have won the match vs A. As F won against A, F won both its matches and C lost both its matches. One more team lost both its matches. As B, E and F have won at least one match and A and C have been discussed previously, D must have lost both matches. Hence, stage 2 results are:

Stage 2: D-B (B won), D-E (E won), E-A (E won), F-A (F won), B-C (B won) and C-F (F won)

Hence, the teams that won both of their stage 2 matches are B, E and F.

Question 3: The teams that won exactly two matches in the event are:

a) A, D & F

b) D & E

c) E & F

d) D, E & F

e) D & F

3) Answer (E)

View Video Solution

Solution:

There are a total of $^6 C_2$ matches => 15 matches. The first 9 matches are held in the first stage and remaining 6 in the second stage.

From the information given, we can conclude that the following matches were held in first stage:

Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won)

One team won all matches. As B, C, D E and F have lost at least one match each, A won all three matches. As A, B, D, E have won at least one match, C and F lost both matches.

From the matches already deduced, we can see that A needs to play 2 more matches, B two more matches and C and F one match each. As C and F lose all matches in stage 1, they cannot play against each other. F did not play against the leader i.e. A. Hence, the remaining matches are A-B (A won), A-C (A won), B-F (B won).

Thus, the stage 1 matches are

Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won), A-B (A won), A-C (A won), B-F (B won)

Thus Stage 2 matches are D-B, D-E, E-A, F-A, B-C and C-F (all matches – stage 1 matches)

As A lost both matches, F and E must have won the match vs A. As F won against A, F won both its matches and C lost both its matches. One more team lost both its matches. As B, E and F have won at least one match and A and C have been discussed previously, D must have lost both matches. Hence, stage 2 results are:

Stage 2: D-B (B won), D-E (E won), E-A (E won), F-A (F won), B-C (B won) and C-F (F won)

Hence, the wins by each team are A (3), B(4), C(0), D(2), E(4), F(2). Hence, D and F won exactly 2 matches.

Question 4: The team(s) with the most wins in the event is (are):

a) A

b) A & C

c) F

d) E

e) B & E

4) Answer (E)

View Video Solution

Solution:

There are a total of $^6 C_2$ matches => 15 matches. The first 9 matches are held in the first stage and remaining 6 in the second stage.

From the information given, we can conclude that the following matches were held in first stage:

Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won)

One team won all matches. As B, C, D E and F have lost at least one match each, A won all three matches. As A, B, D, E have won at least one match, C and F lost both matches.

From the matches already deduced, we can see that A needs to play 2 more matches, B two more matches and C and F one match each. As C and F lose all matches in stage 1, they cannot play against each other. F did not play against the leader i.e. A. Hence, the remaining matches are A-B (A won), A-C (A won), B-F (B won).

Thus, the stage 1 matches are

Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won), A-B (A won), A-C (A won), B-F (B won)

Thus Stage 2 matches are D-B, D-E, E-A, F-A, B-C and C-F (all matches – stage 1 matches)

As A lost both matches, F and E must have won the match vs A. As F won against A, F won both its matches and C lost both its matches. One more team lost both its matches. As B, E and F have won at least one match and A and C have been discussed previously, D must have lost both matches. Hence, stage 2 results are:

Stage 2: D-B (B won), D-E (E won), E-A (E won), F-A (F won), B-C (B won) and C-F (F won)

Hence, the wins by each team are A(3), B(4), C(0), D(2), E(4), F(2). Hence, most wins are by B and E.

Instructions

Directions for the next 5 questions:

Sixteen teams have been invited to participate in the ABC Gold Cup cricket tournament. The tournament is conducted in two stages. In the first stage, the teams are divided into two groups. Each group consists of eight teams, with each team playing every other team in its group exactly once. At the end of the first stage, the top four teams from each group advance to the second stage while the rest are eliminated. The second stage comprises of several rounds. A round involves one match for each team. The winner of a match in a round advances to the next round, while the loser is eliminated, The team that remains undefeated in the second stage is declared the winner and claims the Gold Cup.

The tournament rules are such that each match results in a winner and a loser with no possibility of a tie. In the first stage a team earns one point for each win and no points for a loss. At the end of the first stage teams in each group are ranked on the basis of total points to determine the qualifiers advancing to the next stage. Ties are resolved by a series of complex tie-breaking rules so that exactly four teams from each group advance to the next stage.

Question 5: What is the total number of matches played in the tournament?

a) 28

b) 55

c) 63

d) 35

5) Answer (C)

View Video Solution

Solution:

In 1st stage there were 2 groups each group played 28 matches as $^8C_2$ = 28. So total 56 matches after 1st stage . IN 1st round of stage 2, 4 matches are played and in the next round we have 4 teams .The winner is one who defeats every team out of remaining 3 matches . so 3 matches more needed. In total 56+4+3=63.

Checkout: CAT Free Practice Questions and Videos

Question 6: The minimum number of wins needed for a team in the first stage to guarantee its advancement to the next stage is:

a) 5

b) 6

c) 7

d) 4

6) Answer (B)

View Video Solution

Solution:

Let us first try to find the maximum number of points with which a team cannot advance to the second stage.

For this to happen the top five teams should have highest possible equal number of points and one team does not advance after the tie breaker.

To maximize the points of top 5 teams all of the top 5 teams should win their matches with the bottom 3 teams. Now each team has 3 points.

The top 5 teams play 5C2 = 10 matches among themselves. There are 10 points to be won from these 10 matches.

Now as all the top 5 teams should have equal number of points each team gets 2 points from these games.

In all each top 5 team gets 3+2 = 5 points each.

In this case after getting 5 points also one of the top 5 teams will not advance to the second round.

Thus the maximum number of points with which a team cannot advance to the second stage is 5.

Therefore at least 6 wins are required for a team to guarantee its advancement to the next stage.

Question 7: What is the highest number of wins for a team in the first stage in spite of which it would be eliminated at the end of first stage?

a) 1

b) 2

c) 3

d) 5

7) Answer (D)

View Video Solution

Solution:

There are 28 matches in the 1st round of 8 player group so in total 28 wins.To find this, we need the top 5 teams to win nearly equal matches. So Let each of the top 5 teams win 5 matches each and the remaining 3 matches are won by the bottom 2 teams. The qualifiers will be decided based on the tie breaking rules. Hence, even with 5 wins a team may end up not qualifying for the next round. Thus, option D is the correct answer.

Question 8: What is the number of rounds in the second stage of the tournament?’

a) 1

b) 2

c) 3

d) 4

8) Answer (C)

View Video Solution

Solution:

2nd stage 1st round has 8 teams , 2nd round will have 4 teams and 3rd round 2 teams where the winner wins .

Question 9: Which of the following statements is true?

a) The winner will have more wins than any other team in the tournament.

b) At the end of the first stage, no team eliminated from the tournament will have more wins than any of the teams qualifying for the second stage.

c) It is possible that the winner will have the same number of wins in the entire tournament as a team eliminated at the end of the first stage.

d) The number of teams with exactly one win in the second stage of the tournament is 4.

9) Answer (C)

View Video Solution

Solution:

Consider the below case.

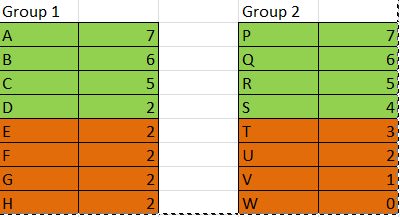
If D wins the tournament he would have 5 wins. But if P loses in second round, he would have 7 wins. Hence option A is incorrect.

We can see that T has more wins than D. Hence option B is incorrect.

Consider the below scenario:

We can see that 2 teams have one win each in the second stage. Hence option D is incorrect.

Consider the following scenario.

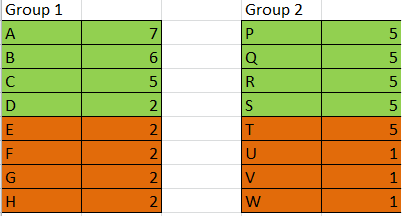
If D wins the tournament he would have 5 wins. But T would lose the tournament with 5 wins. Hence option C is correct.

Instructions

The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo. The bids are made simultaneously. If all four bid Hi, then all four lose 1 point each. If three players bid Hi and one bids Lo, then the players bidding Hi gain 1 point each and the player bidding Lo loses 3 points. If two players bid Hi and two bid Lo, then the players bidding Hi gain 2 points each and the players bidding Lo lose 2 points each. If one player bids Hi and three bid Lo, then the player bidding Hi gains 3 points and the players bidding Lo lose 1 point each. If all four bid Lo, then all four gain 1 point each. Four players Arun, Bankim, Charu, and Dipak played the Hi-Lo game. The following facts are known about their game:

1. At the end of three rounds, Arun had scored 6 points, Dipak had scored 2 points, Bankim and Charu had scored -2 points each.
2. At the end of six rounds, Arun had scored 7 points, Bankim and Dipak had scored -1 point each, and Charu had scored -5 points.
3. Dipak’s score in the third round was less than his score in the first round but was more than his score in the second round.
4. In exactly two out of the six rounds, Arun was the only player who bid Hi.

Question 10: What were the bids by Arun, Bankim, Charu and Dipak, respectively in the first round?

a) Hi, Lo, Lo, Hi

b) Hi, Lo, Lo, Lo

c) Hi, Hi, Lo, Lo

d) Lo, Lo, Lo, Hi

10) Answer (A)

View Video Solution

Solution:

Let ‘H’ represents Hi and ‘L’ represents Lo.

Given if they bid

Case 1: HHHH then all players gets -1 points.

Case 2: HHHL => H gets +1 and L gets -3.

Case 3: HHLL => H gets +2 and L gets -2.

Case 4: HLLL => H gets +3 and L gets -1.

Case 5: LLLL => every player gets +1.

From the given information we can draw the following table:

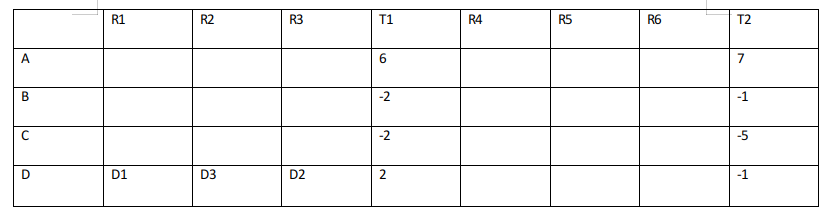
**T1 is the cumulative of points till Round 3 and T2 is sum of points till round 6.

**Arun, Bankim, Charu, and Dipak are represented by A, B, C, D respectively.

From point 3, D1>D2>D3

D scored 2 points till round R3 and D1>D3>D2 the possible scenarios are :

Case D1: 3,2,-3

In this case the points of A in R1, R3, R2 will be -1,2/-2, 1 in any
possible combination the sum will not be 6. So, this case is invalid.

Case D2: 2,1,-1

In this case the points of A in R1, R3, R2 will be 2/-2, 1/-3, -1/3
so, if the points in R1, R3, R2 are 2,1,3 the case is valid and no other
cases are possible.

Case D3: 3,1,-2

In this case the points of A in R1, R3, R2 will be -1, 1/-3/1, 2/-2
in any possible combination the sum will not be 6. So, this case is
invalid.

.’. Points of A,D in (R1,R2,R3) are (2,3,1) and (2,-1,1) respectively.

Since A got +3 in R2, he is only the one to bid h in R2 and points of B and C in round 2 are -1,-1 i.e they bid L, L.

Since A and D got 2 points each in R1, C and B must have got -2, -2 i.e they bid L, L.

Since A and D got 1 point in R3, C and B must also have got 1 in R3 i.e they bid L, L.

With this data, the table now looks like:

No information is given about the individual scores in R4, R5, R6.

Given In exactly two out of the six rounds, Arun was the only player who bid Hi.

Let R.x, R.y, R.z represent R4, R5, R6 in any order.

Let A bid H in R.x=> B,C,D bid L.

The table now looks like:

For A, R.x+R.y+R.z=1 => R.y+R.z=-2

For B, R.x+R.y+R.z=1 => R.y+R.z=2

For C, R.x+R.y+R.z=-3 => R.y+R.z=-2

For D, R.x+R.y+R.z=-3.=> R.y+R.z=-2

(R.y, R.z) for A can be (-3,1) or (-1,-1)

Case A1:

If for A, (R.y, R.z)=(-3,1)

Since for both C,D: R.y+R.z=-2

We can’t get any combination such that the total points of B,C,D are obtained.

Case A2:

If for A, (R.y, R.z)=(-1,-1).the (R.y, R.z) of B,C,D can be (3,-1), (-1,-1), (-1,-1) and they must have bid (H,H), (L,H), (L,H) respectively while A must have bid (L, H)

Hence this case is valid.

The final table looks like:

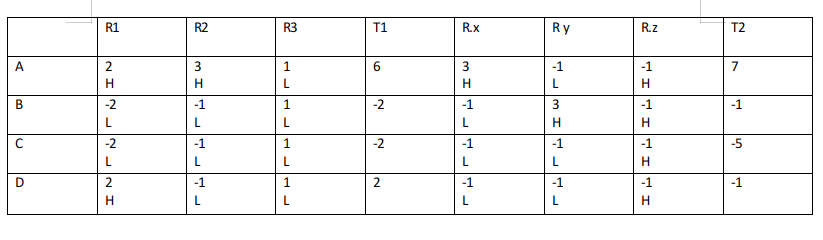
The bids by Arun, Bankim, Charu and Dipak, respectively in the first round are HLLH.

Hence Option A is correct.

Question 11: In how many rounds did Arun bid Hi?

11) Answer: 4

View Video Solution

Solution:

Let ‘H’ represents Hi and ‘L’ represents Lo.

Given if they bid

Case 1: HHHH then all players gets -1 points.

Case 2: HHHL => H gets +1 and L gets -3.

Case 3: HHLL => H gets +2 and L gets -2.

Case 4: HLLL => H gets +3 and L gets -1.

Case 5: LLLL => every player gets +1.

From the given information we can draw the following table:

**T1 is the cumulative of points till Round 3 and T2 is sum of points till round 6.

**Arun, Bankim, Charu, and Dipak are represented by A, B, C, D respectively.

From point 3, D1>D2>D3

D scored 2 points till round R3 and D1>D3>D2 the possible scenarios are :

Case D1: 3,2,-3

In this case the points of A in R1, R3, R2 will be -1,2/-2, 1 in any
possible combination the sum will not be 6. So, this case is invalid.

Case D2: 2,1,-1

In this case the points of A in R1, R3, R2 will be 2/-2, 1/-3, -1/3
so, if the points in R1, R3, R2 are 2,1,3 the case is valid and no other
cases are possible.

Case D3: 3,1,-2

In this case the points of A in R1, R3, R2 will be -1, 1/-3/1, 2/-2
in any possible combination the sum will not be 6. So, this case is
invalid.

.’. Points of A,D in (R1,R2,R3) are (2,3,1) and (2,-1,1) respectively.

Since A got +3 in R2, he is only the one to bid h in R2 and points of B and C in round 2 are -1,-1 i.e they bid L, L.

Since A and D got 2 points each in R1, C and B must have got -2, -2 i.e they bid L, L.

Since A and D got 1 point in R3, C and B must also have got 1 in R3 i.e they bid L, L.

With this data, the table now looks like:

No information is given about the individual scores in R4, R5, R6.

Given In exactly two out of the six rounds, Arun was the only player who bid Hi.

Let R.x, R.y, R.z represent R4, R5, R6 in any order.

Let A bid H in R.x=> B,C,D bid L.

The table now looks like:

For A, R.x+R.y+R.z=1 => R.y+R.z=-2

For B, R.x+R.y+R.z=1 => R.y+R.z=2

For C, R.x+R.y+R.z=-3 => R.y+R.z=-2

For D, R.x+R.y+R.z=-3.=> R.y+R.z=-2

(R.y, R.z) for A can be (-3,1) or (-1,-1)

Case A1:

If for A, (R.y, R.z)=(-3,1)

Since for both C,D: R.y+R.z=-2

We can’t get any combination such that the total points of B,C,D are obtained.

Case A2:

If for A, (R.y, R.z)=(-1,-1).the (R.y, R.z) of B,C,D can be (3,-1),
(-1,-1), (-1,-1) and they must have bid (H,H), (L,H), (L,H) respectively
while A must have bid (L, H)

Hence this case is valid.

The final table looks like:

Arun bid high in R1,R2, R.x, R.z hence, 4 is correct answer.

Question 12: In how many rounds did Bankim bid Lo?

12) Answer: 4

View Video Solution

Solution:

Let ‘H’ represents Hi and ‘L’ represents Lo.

Given if they bid

Case 1: HHHH then all players gets -1 points.

Case 2: HHHL => H gets +1 and L gets -3.

Case 3: HHLL => H gets +2 and L gets -2.

Case 4: HLLL => H gets +3 and  L gets -1.

Case 5: LLLL => every player gets +1.

From the given information we can draw the following table:

**T1 is the cumulative of points till Round 3 and T2 is sum of points till round 6.

**Arun, Bankim, Charu, and Dipak are represented by A, B, C, D respectively.

From point 3, D1>D2>D3

D scored 2 points till round R3 and D1>D3>D2 the possible scenarios are :

Case D1: 3,2,-3

In this case the points of A in  R1, R3, R2 will be -1,2/-2, 1 in any possible combination the sum will not be 6. So, this case is invalid.

Case D2: 2,1,-1

In this case the points of A in R1, R3, R2 will be 2/-2, 1/-3, -1/3 so, if the points in R1, R3, R2 are 2,1,3 the case is valid and no other cases are possible.

Case D3: 3,1,-2

In this case the points of A in R1, R3, R2 will be -1, 1/-3/1, 2/-2 in any possible combination the sum will not be 6. So, this case is invalid.

.’. Points of A,D in (R1,R2,R3) are (2,3,1) and (2,-1,1) respectively.

Since A got +3 in R2, he is only the one to bid h in R2 and points of B and C in round 2 are -1,-1 i.e they bid L, L.

Since A and D got 2 points each in R1, C and B must have got -2, -2 i.e they bid L, L.

Since A and D got 1 point in R3, C and B must also have got 1 in R3 i.e they bid L, L.

With this data, the table now looks like:

No information is given about the individual scores in R4, R5, R6.

Given In exactly two out of the six rounds, Arun was the only player who bid Hi.

Let R.x, R.y, R.z represent R4, R5, R6 in any order.

Let A bid H in R.x=> B,C,D bid L.

The table now looks like:

For A, R.x+R.y+R.z=1 => R.y+R.z=-2

For B, R.x+R.y+R.z=1 => R.y+R.z=2

For C, R.x+R.y+R.z=-3 => R.y+R.z=-2

For D, R.x+R.y+R.z=-3.=> R.y+R.z=-2

(R.y, R.z) for A can be (-3,1) or (-1,-1)

Case A1:

If for A, (R.y, R.z)=(-3,1)

Since for both C,D: R.y+R.z=-2

We can’t get any combination such that the total points of B,C,D are obtained.

Case A2:

If for A, (R.y, R.z)=(-1,-1).the (R.y, R.z) of B,C,D can be (3,-1), (-1,-1), (-1,-1) and they must have bid (H,H), (L,H), (L,H) respectively while A must have bid (L, H)

Hence this case is valid.

The final table looks like:

Bikram bid Lo in R1,R2,R3,R.x. Hence 4 is correct answer.

Question 13: In how many rounds did all four players make identical bids?

13) Answer: 2

View Video Solution

Solution:

Let ‘H’ represents Hi and ‘L’ represents Lo.

Given if they bid

Case 1: HHHH then all players gets -1 points.

Case 2: HHHL => H gets +1 and L gets -3.

Case 3: HHLL => H gets +2 and L gets -2.

Case 4: HLLL => H gets +3 and L gets -1.

Case 5: LLLL => every player gets +1.

From the given information we can draw the following table:

**T1 is the cumulative of points till Round 3 and T2 is sum of points till round 6.

**Arun, Bankim, Charu, and Dipak are represented by A, B, C, D respectively.

From point 3, D1>D2>D3

D scored 2 points till round R3 and D1>D3>D2 the possible scenarios are :

Case D1: 3,2,-3

In this case the points of A in R1, R3, R2 will be -1,2/-2, 1 in any
possible combination the sum will not be 6. So, this case is invalid.

Case D2: 2,1,-1

In this case the points of A in R1, R3, R2 will be 2/-2, 1/-3, -1/3
so, if the points in R1, R3, R2 are 2,1,3 the case is valid and no other
cases are possible.

Case D3: 3,1,-2

In this case the points of A in R1, R3, R2 will be -1, 1/-3/1, 2/-2
in any possible combination the sum will not be 6. So, this case is
invalid.

.’. Points of A,D in (R1,R2,R3) are (2,3,1) and (2,-1,1) respectively.

Since A got +3 in R2, he is only the one to bid h in R2 and points of B and C in round 2 are -1,-1 i.e they bid L, L.

Since A and D got 2 points each in R1, C and B must have got -2, -2 i.e they bid L, L.

Since A and D got 1 point in R3, C and B must also have got 1 in R3 i.e they bid L, L.

With this data, the table now looks like:

No information is given about the individual scores in R4, R5, R6.

Given In exactly two out of the six rounds, Arun was the only player who bid Hi.

Let R.x, R.y, R.z represent R4, R5, R6 in any order.

Let A bid H in R.x=> B,C,D bid L.

The table now looks like:

For A, R.x+R.y+R.z=1 => R.y+R.z=-2

For B, R.x+R.y+R.z=1 => R.y+R.z=2

For C, R.x+R.y+R.z=-3 => R.y+R.z=-2

For D, R.x+R.y+R.z=-3.=> R.y+R.z=-2

(R.y, R.z) for A can be (-3,1) or (-1,-1)

Case A1:

If for A, (R.y, R.z)=(-3,1)

Since for both C,D: R.y+R.z=-2

We can’t get any combination such that the total points of B,C,D are obtained.

Case A2:

If for A, (R.y, R.z)=(-1,-1).the (R.y, R.z) of B,C,D can be (3,-1),
(-1,-1), (-1,-1) and they must have bid (H,H), (L,H), (L,H) respectively
while A must have bid (L, H)

Hence this case is valid.

The final table looks like:

All the players made identical bids in R3 and R.z

Question 14: In how many rounds did Dipak gain exactly 1 point?

14) Answer: 1

View Video Solution

Solution:

Let ‘H’ represents Hi and ‘L’ represents Lo.

Given if they bid

Case 1: HHHH then all players gets -1 points.

Case 2: HHHL => H gets +1 and L gets -3.

Case 3: HHLL => H gets +2 and L gets -2.

Case 4: HLLL => H gets +3 and L gets -1.

Case 5: LLLL => every player gets +1.

From the given information we can draw the following table:

**T1 is the cumulative of points till Round 3 and T2 is sum of points till round 6.

**Arun, Bankim, Charu, and Dipak are represented by A, B, C, D respectively.

From point 3, D1>D2>D3

D scored 2 points till round R3 and D1>D3>D2 the possible scenarios are :

Case D1: 3,2,-3

In this case the points of A in R1, R3, R2 will be -1,2/-2, 1 in any
possible combination the sum will not be 6. So, this case is invalid.

Case D2: 2,1,-1

In this case the points of A in R1, R3, R2 will be 2/-2, 1/-3, -1/3
so, if the points in R1, R3, R2 are 2,1,3 the case is valid and no other
cases are possible.

Case D3: 3,1,-2

In this case the points of A in R1, R3, R2 will be -1, 1/-3/1, 2/-2
in any possible combination the sum will not be 6. So, this case is
invalid.

.’. Points of A,D in (R1,R2,R3) are (2,3,1) and (2,-1,1) respectively.

Since A got +3 in R2, he is only the one to bid h in R2 and points of B and C in round 2 are -1,-1 i.e they bid L, L.

Since A and D got 2 points each in R1, C and B must have got -2, -2 i.e they bid L, L.

Since A and D got 1 point in R3, C and B must also have got 1 in R3 i.e they bid L, L.

With this data, the table now looks like:

No information is given about the individual scores in R4, R5, R6.

Given In exactly two out of the six rounds, Arun was the only player who bid Hi.

Let R.x, R.y, R.z represent R4, R5, R6 in any order.

Let A bid H in R.x=> B,C,D bid L.

The table now looks like:

For A, R.x+R.y+R.z=1 => R.y+R.z=-2

For B, R.x+R.y+R.z=1 => R.y+R.z=2

For C, R.x+R.y+R.z=-3 => R.y+R.z=-2

For D, R.x+R.y+R.z=-3.=> R.y+R.z=-2

(R.y, R.z) for A can be (-3,1) or (-1,-1)

Case A1:

If for A, (R.y, R.z)=(-3,1)

Since for both C,D: R.y+R.z=-2

We can’t get any combination such that the total points of B,C,D are obtained.

Case A2:

If for A, (R.y, R.z)=(-1,-1).the (R.y, R.z) of B,C,D can be (3,-1),
(-1,-1), (-1,-1) and they must have bid (H,H), (L,H), (L,H) respectively
while A must have bid (L, H)

Hence this case is valid.

The final table looks like:

Deepak got exactly one point in only R3.

Hence 1 is correct answer.

Question 15: In which of the following rounds, was Arun DEFINITELY the only player to bid Hi?

a) Second

b) Third

c) Fourth

d) First

15) Answer (A)

View Video Solution

Solution:

Let ‘H’ represents Hi and ‘L’ represents Lo.

Given if they bid

Case 1: HHHH then all players gets -1 points.

Case 2: HHHL => H gets +1 and L gets -3.

Case 3: HHLL => H gets +2 and L gets -2.

Case 4: HLLL => H gets +3 and L gets -1.

Case 5: LLLL => every player gets +1.

From the given information we can draw the following table:

**T1 is the cumulative of points till Round 3 and T2 is sum of points till round 6.

**Arun, Bankim, Charu, and Dipak are represented by A, B, C, D respectively.

From point 3, D1>D2>D3

D scored 2 points till round R3 and D1>D3>D2 the possible scenarios are :

Case D1: 3,2,-3

In this case the points of A in R1, R3, R2 will be -1,2/-2, 1 in any
possible combination the sum will not be 6. So, this case is invalid.

Case D2: 2,1,-1

In this case the points of A in R1, R3, R2 will be 2/-2, 1/-3, -1/3
so, if the points in R1, R3, R2 are 2,1,3 the case is valid and no other
cases are possible.

Case D3: 3,1,-2

In this case the points of A in R1, R3, R2 will be -1, 1/-3/1, 2/-2
in any possible combination the sum will not be 6. So, this case is
invalid.

.’. Points of A,D in (R1,R2,R3) are (2,3,1) and (2,-1,1) respectively.

Since A got +3 in R2, he is only the one to bid h in R2 and points of B and C in round 2 are -1,-1 i.e they bid L, L.

Since A and D got 2 points each in R1, C and B must have got -2, -2 i.e they bid L, L.

Since A and D got 1 point in R3, C and B must also have got 1 in R3 i.e they bid L, L.

With this data, the table now looks like:

No information is given about the individual scores in R4, R5, R6.

Given In exactly two out of the six rounds, Arun was the only player who bid Hi.

Let R.x, R.y, R.z represent R4, R5, R6 in any order.

Let A bid H in R.x=> B,C,D bid L.

The table now looks like:

For A, R.x+R.y+R.z=1 => R.y+R.z=-2

For B, R.x+R.y+R.z=1 => R.y+R.z=2

For C, R.x+R.y+R.z=-3 => R.y+R.z=-2

For D, R.x+R.y+R.z=-3.=> R.y+R.z=-2

(R.y, R.z) for A can be (-3,1) or (-1,-1)

Case A1:

If for A, (R.y, R.z)=(-3,1)

Since for both C,D: R.y+R.z=-2

We can’t get any combination such that the total points of B,C,D are obtained.

Case A2:

If for A, (R.y, R.z)=(-1,-1).the (R.y, R.z) of B,C,D can be (3,-1),
(-1,-1), (-1,-1) and they must have bid (H,H), (L,H), (L,H) respectively
while A must have bid (L, H)

Hence this case is valid.

The final table looks like:

R2 is correct answer.