CAT Geometry (Triangles) Questions PDF [Most Expected]
Geometry Triangles questions are important concepts in the Geometry concept of the CAT Quant section. These questions are not very tough; make sure you are aware of all the Important Formulas in CAT Geometry. Solve more questions from CAT Geometry Triangles. You can check out these CAT Geometry questions from the CAT Previous year papers. Practice a good number of questions in CAT Geometry Triangles so that you can answer these questions with ease in the exam. In this post, we will look into some important CAT Geometry Questions. These are a good source of practice for CAT 2022 preparation; If you want to practice these questions, you can download these Important Triangles (Geometry) Questions for CAT (with detailed answers) PDF along with the video solutions below, which is completely Free.
Download Triangles Geometry Questions for CAT
Question 1: In a triangle ABC, the lengths of the sides AB and AC equal 17.5 cm and 9 cm respectively. Let D be a point on the line segment BC such that AD is perpendicular to BC. If AD = 3 cm, then what is the radius (in cm) of the circle circumscribing the triangle ABC?
a) 17.05
b) 27.85
c) 22.45
d) 32.25
e) 26.25
1) Answer (E)
Solution:
Let x be the value of third side of the triangle. Now we know that Area = 17.5*9*x/(4*R), where R is circumradius.
Also Area = 0.5*x*3 .
Equating both, we have 3 = 17.5*9 / (2*R)
=> R = 26.25.
Question 2: Consider obtuse-angled triangles with sides 8 cm, 15 cm and x cm. If x is an integer then how many such triangles exist?
a) 5
b) 21
c) 10
d) 15
e) 14
2) Answer (C)
Solution:
For obtuse-angles triangle, $c^2 > a^2 + b^2$ and c < a+b
If 15 is the greatest side, 8+x > 15 => x > 7 and $225 > 64 + x^2$ => $x^2$ < 161 => x <= 12
So, x = 8, 9, 10, 11, 12
If x is the greatest side, then 8 + 15 > x => x < 23
$x^2 > 225 + 64 = 289$ => x > 17
So, x = 18, 19, 20, 21, 22
So, the number of possibilities is 10
Question 3: In the figure below, ABCDEF is a regular hexagon and $\angle{AOF}$ = 90° . FO is parallel to ED. What is the ratio of the area of the triangle AOF to that of the hexagon ABCDEF?
a) 1/12
b) 1/6
c) 1/24
d) 1/18
3) Answer (A)
Solution:
When the hexagon is divided into number of similar triangle AOF we get 12 such triangles . Hence required ratio of area is 1/12.
Alternate Approach :
Let us take side of the hexagon as a
Now We get AF = a
Now As OF || ED
Angle OFE +Angle E = 180
We know Angle E =120
So angle OFE=60 degrees.
Now therefore Angle AFO=120-60=60 degrees
Now in triangle AFO
Cos60=$\frac{OF}{AF}$
$\frac{1}{2}=\frac{OF}{AF}$
We get OF = $\frac{a}{2}$
Now therefore area of triangle AOF =$\frac{1}{2}\times\ AF\times\ OF\times\ \sin60$
So we get $\frac{1}{2}\times\ a\times\ \frac{a}{2}\times\ \frac{\sqrt{\ 3}}{2}$
=$\frac{\sqrt{\ 3}}{8}a^2$ (1)
Now area of hexagon = $6\times\ \frac{\sqrt{\ 3}}{4}a^2$ (2)
Dividing (1) and (2) we get ratio as $\frac{1}{12}$
Hence option A is the correct answer.
Question 4: If the lengths of diagonals DF, AG and CE of the cube shown in the adjoining figure are equal to the three sides of a triangle, then the radius of the circle circumscribing that triangle will be?
a) equal to the side of the cube
b) $\sqrt 3$ times the side of the cube
c) 1/$\sqrt 3$ times the side of the cube
d) impossible to find from the given information
4) Answer (A)
Solution:
Consider side of the cube as x.
So diagonal will be of length $\sqrt{3}$ * x.
Now if diagonals are side of equilateral triangle we get area = 3*$\sqrt{3}*x^2$ /4 .
Also in a triangle
4 * Area * R = Product of sides
4* 3*$\sqrt{3}*x^2$ /4 * R = .3*$\sqrt{3}*x^3$
R = x
Question 5: In triangle DEF shown below, points A, B and C are taken on DE, DF and EF respectively such that EC = AC and CF = BC. If angle D equals 40 degress , then angle ACB is ?
a) 140
b) 70
c) 100
d) None of these
5) Answer (C)
Solution:
Let angle EAC = x, so angle AEC = x and angle ACE = 180-2x
Let angle FBC = y, so angle BFC = y and angle BCF = 180-2y
So, angle ACB = 180-(180-2x+180-2y) = 2(x+y) – 180
x+y = 180 – 40 = 140
So, angle ACB = 280 – 180 = 100
Question 6: If a,b,c are the sides of a triangle, and $a^2 + b^2 +c^2 = bc + ca + ab$, then the triangle is:
a) equilateral
b) isosceles
c) right angled
d) obtuse angled
6) Answer (A)
Solution:
$(a+b+c)^2 = a^2 + b^2 + c^2 + 2(ab + bc + ca) => 3(a^2 + b^2 + c^2)$
This is possible only if a = b = c.
So, the triangle is an equilateral triangle.
Question 7: In the figure given below, ABCD is a rectangle. The area of the isosceles right triangle ABE = 7 $cm^2$ ; EC = 3(BE). The area of ABCD (in $cm^2$) is
a) 21 $cm^2$
b) 28 $cm^2$
c) 42 $cm^2$
d) 56 $cm^2$
7) Answer (D)
Solution:
Let AB = BE = x
Area of triangle ABE = $x^2/2$ = 14; we get x = $\sqrt{14}$
So we have side BC = 4*$\sqrt{14}$
Now area is AB*BC = 14 *4 = 56 $cm^2$
Question 8: The area of the triangle whose vertices are (a,a), (a + 1, a + 1) and (a + 2, a) is
[CAT 2002]
a) $a^3$
b) $1$
c) $2a$
d) $2^{1/2}$
8) Answer (B)
Solution:
The triangle we have is :
The length of three sides is $\sqrt 2, \sqrt 2$ and $2$.
This is a right-angled triangle.
Hence, it’s area equals $1/2 * \sqrt 2 * \sqrt 2 = 1$
So, the correct answer is b)
Alternate Approach :
Area of triangle = $\frac{1}{2}\times\ base\times\ height$
So we get $\frac{1}{2}\times2\times\ 1$=1 square units
Question 9: In the following figure, ACB is a right-angled triangle. AD is the altitude. Circles are inscribed within the triangle ACD and triangle BCD. P and Q are the centers of the circles. The distance PQ is
The length of AB is 15 m and AC is 20 m
a) 7 m
b) 4.5 m
c) 10.5 m
d) 6 m
9) Answer (A)
Solution:
By Pythagoras theorem we get BC = 25 . Let BD = x;Triangle ABD is similar to triangle CBA => AD/15 = x/20 and also triangle ADC is similar to triangle ACB=> AD/20 = (25-x)/15. From the 2 equations, we get x = 9 and DC = 16
We know that AREA = (semi perimeter ) * inradius
For triangle ABD, Area = 1/2 x BD X AD = 1/2 x 12 x 9 = 54 and semi perimeter = (15 + 9 + 12)/2 = 18. On using the above equation we get, inradius, r = 3.
Similarly for triangle ADC we get inradius R = 4 .
PQ = R + r = 7 cm
Question 10: If ABCD is a square and BCE is an equilateral triangle, what is the measure of ∠DEC?
a) 15°
b) 30°
c) 20°
d) 45°
10) Answer (A)
Solution:
According to given diagram, as triangle BCE is equilateral CE=BE=DC
Hence angle CDE = angle CED
So angle DEC = $\frac{180-150}{2} = 15$
Question 11: In triangleABC, ∠B is a right angle, AC = 6 cm, and D is the mid-point of AC. The length of BD is
a) 4cm
b) 6 cm
c) 3cm
d) 3.5cm
11) Answer (C)
Solution:
A circle is circumscribed to triangle ABC.
For this circle D will be centre of circle, and AD , DC , BD will radius of this circle.
Hence AD=BD=DC=3 cm
Question 12: From a triangle ABC with sides of lengths 40 ft, 25 ft and 35 ft, a triangular portion GBC is cut off where G is the centroid of ABC. The area, in sq ft, of the remaining portion of triangle ABC is
a) $225\sqrt{3}$
b) $\frac{500}{\sqrt{3}}$
c) $\frac{275}{\sqrt{3}}$
d) $\frac{250}{\sqrt{3}}$
12) Answer (B)
Solution:
The lengths are given as 40, 25 and 35.
The perimeter = 100
Semi-perimeter, s = 50
Area = $ \sqrt{50 * 10 * 25 * 15}$ = $250\sqrt{3}$
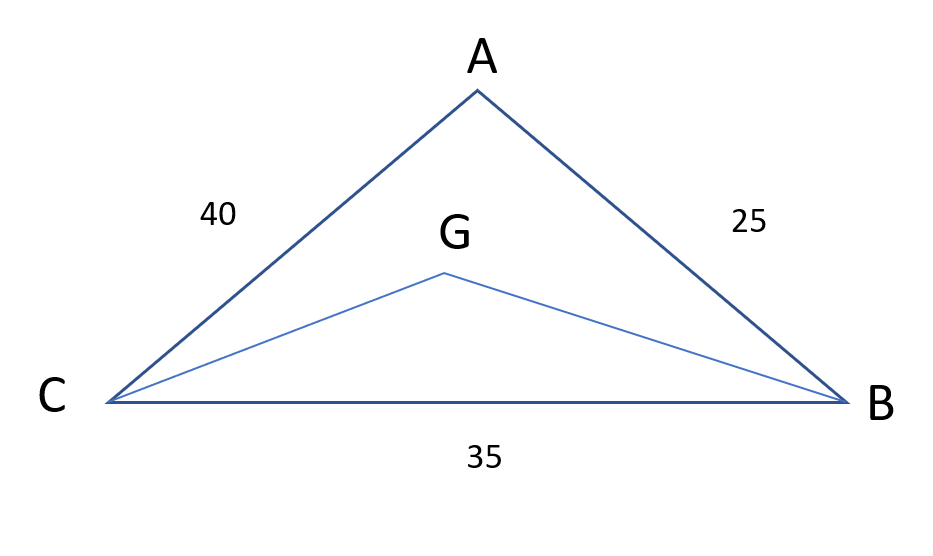
The triangle formed by the centroid and two vertices is removed.
Since the cenroid divides the median in the ratio 2 : 1
The remaining area will be two-thirds the area of the original triangle.
Remaining area = $\frac{2}{3} * 250\sqrt{3}$ = $\frac{500}{\sqrt{3}}$
Question 13: Let ABC be a right-angled triangle with BC as the hypotenuse. Lengths of AB and AC are 15 km and 20 km, respectively. The minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour is
13) Answer: 24
Solution:
The length of the altitude from A to the hypotenuse will be the shortest distance.
This is a right triangle with sides 3 : 4 : 5.
Hence, the hypotenuse = $\sqrt{20^2+15^2}$ = 25 Km.
Length of the altitude = $\frac{15 * 20}{25}$ = 12 Km
(This is derived from equating area of triangle, $\frac{15\cdot20}{2}\ =\ \frac{25\cdot\text{altitude}}{2}$)
The time taken = $\frac{12}{30} * 60$ = 24 minutes
