Geometry Triangle Questions for CAT

Geometry Triangle is one of the most important topics in the CAT Quants section. If you’re weak in Geometry Triangle questions for CAT, make sure you learn all the basic concepts of solving the questions and also all the important formulas of TSD. Here, you can learn all the important concepts in CAT Geometry Triangle. You can check out these CAT Time and Work questions from the CAT Previous year’s papers. This post will look at important Geometry Triangle questions in the CAT quant section. These are a good source of practice for CAT preparation; If you want to practice these questions, you can download this CAT TSD Questions PDF along with the detailed solutions (and video solutions) below, which is completely Free.

Download Geometry Triangle Questions for CAT

Enroll for CAT 2023 Online Course

Question 1: In a triangle ABC, the lengths of the sides AB and AC equal 17.5 cm and 9 cm respectively. Let D be a point on the line segment BC such that AD is perpendicular to BC. If AD = 3 cm, then what is the radius (in cm) of the circle circumscribing the triangle ABC?

a) 17.05

b) 27.85

c) 22.45

d) 32.25

e) 26.25

1) Answer (E)

View Video Solution

Solution:

Let x be the value of third side of the triangle. Now we know that Area = 17.5*9*x/(4*R), where R is circumradius.

Also Area = 0.5*x*3 .

Equating both, we have 3 = 17.5*9 / (2*R)

=> R = 26.25.

Question 2: Consider obtuse-angled triangles with sides 8 cm, 15 cm and x cm. If x is an integer then how many such triangles exist?

a) 5

b) 21

c) 10

d) 15

e) 14

2) Answer (C)

View Video Solution

Solution:

For obtuse-angles triangle, $c^2 > a^2 + b^2$ and c < a+b
If 15 is the greatest side, 8+x > 15 => x > 7 and $225 > 64 + x^2$ => $x^2$ < 161 => x <= 12
So, x = 8, 9, 10, 11, 12
If x is the greatest side, then 8 + 15 > x => x < 23
$x^2 > 225 + 64 = 289$ => x > 17
So, x = 18, 19, 20, 21, 22
So, the number of possibilities is 10

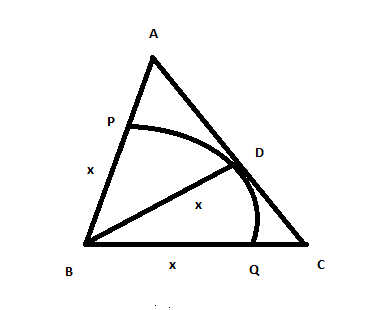
Question 3: In the triangle ABC, AB = 6, BC = 8 and AC = 10. A perpendicular dropped from B, meets the side AC at D. A circle of radius BD (with center B) is drawn. If the circle cuts AB and BC at P and Q respectively, the AP:QC is equal to

a) 1:1

b) 3:2

c) 4:1

d) 3:8

3) Answer (D)

View Video Solution

Solution:

Let BD = x .Semi-perimeter of triangle ABC = 12. Now by herons formula area of ABC is 24. Also Area = 0.5*x*10 . We get x = 24/5 .  AP = 6/5  and CQ = 16/5 . Hence the required ratio is 3:8.

Question 4: An equilateral triangle DOC is drawn inside a square ABCD. What is the value of the angle AOB in degrees?

a) 75

b) 90

c) 120

d) 135

e) 150

4) Answer (E)

View Video Solution

Solution:

Triangle AOD is isosceles. So, angle DAO = angle DOA = 75. Similarly, angle BOC = 75. So, angle AOB = 150

Question 5: What is the distance in cm between two parallel chords of lengths 32 cm and 24 cm in a circle of radius 20 cm?

a) 1 or 7

b) 2 or 14

c) 3 or 21

d) 4 or 28

5) Answer (D)

View Video Solution

Solution:

The distances of the chords from the center are 12 cm and 16 cm respectively.

If the chords lie on the same side of the center, the distance between the chords is 4 cm, if they lie on opposite sides of the center, the distance between them is 28 cm.

Checkout: CAT Free Practice Questions and Videos

Question 6: Consider a triangle drawn on the X-Y plane with its three vertices at (41, 0), (0, 41) and (0, 0), each vertex being represented by its (X,Y) coordinates. The number of points with integer coordinates inside the triangle (excluding all the points on the boundary) is

a) 780

b) 800

c) 820

d) 741

6) Answer (A)

View Video Solution

Solution:

The number of points on x = 1 is 39. The number of points on x = 2 is 38 and so on till x = 39, which has one point.

So, the total is 1+2+3+…+39 = $\frac{39*40}{2}$ = 780.

Question 7: Consider the triangle ABC shown in the following figure where BC = 12 cm, DB = 9 cm, CD = 6 and $\angle{BCD} = \angle{BAC}$
What is the ratio of the perimeter of the triangle ADC to that of the triangle BDC?

a) 7/9

b) 8/9

c) 6/9

d) 5/9

7) Answer (A)

View Video Solution

Solution:

Consider triangles ABC and BDC
Angle B is common in both triangles. Also $\angle A = \angle C$
Since 2 angles are equal, the third angles $\angle{ACB} = \angle{BDC}$
Hence, triangle BCA $\sim$ BDC (BCA and BDC are similar)
AC/DC = BC/BD = AB/BC
BC = 12 cm, DB = 9 cm, CD = 6 cm
=> AC = 12/9 * 6 = 8 cm
AB = 8/6 * 12 = 16 cm
So, AD = 16 – 9 = 7 cm
Perimeter of ADC = 7+8+6 = 21 cm
Perimeter of BCD = 27 cm
Ratio = 21/27 = 7/9

Checkout: CAT Free Practice Questions and Videos

Question 8: P, Q, S, and R are points on the circumference of a circle of radius r, such that PQR is an equilateral triangle and PS is a diameter of the circle. What is the perimeter of the quadrilateral PQSR?

a) $2r(1+ \sqrt3)$

b) $2r(2+ \sqrt3)$

c) $r(1+ \sqrt5)$

d) $2r+ \sqrt3$

8) Answer (A)

View Video Solution

Solution:

Let PQR be an equilateral triangle with side equal to x and let the intersection point of PS and QR be M.

Clearly, the circle is the circumcircle of the triangle PQR.

QR = x => QM = $\frac{x}{2}$ because a perpendicular from the centre to any chord bisects the chord.

Angle OQM = 30 degrees and QM is equal to $\frac{x}{2}$ => OQ = $\frac{\frac{x}{2}}{cos(30)}$ = $\frac{x}{\sqrt{3}}$

Hence the radius of the circumcircle of an equilateral triangle is equal to $\frac{x}{\sqrt{3}}$.

Angle PQS = 90 degrees as it is an angle in a semicircle. PS bisects angle QPR => angle QPS is 30 degrees. Hence QS subtends an angle of 30 degrees in the major arc => QS subtends an angle of 60 degrees at the centre because angle subtended by a chord at the centre is twice the angle subtended by the chord in the major arc.

Angle QOS = 60 degrees => Triangle QOS is equilateral and hence QS is equal to radius of the circle => QS = $\frac{x}{\sqrt{3}}$

Given that radius is r => r = $\frac{x}{\sqrt{3}}$ => x = $r\sqrt{3}$

=> Perimeter of PQRS = PQ+QS+SR+RP= $ r\sqrt{3} + r + r + r\sqrt{3}$ = $2r(1+\sqrt{3})$

Question 9: Euclid has a triangle in mind. Its longest side has length 20 and another of its sides has length 10. Its area is 80. What is the exact length of its third side?

a) $\sqrt {260}$

b) $\sqrt {250}$

c) $\sqrt {240}$

d) $\sqrt {270}$

9) Answer (A)

View Video Solution

Solution:

We know that area = 0.5*h*10 ; we get h = 16=oa.

Using pythagoras we find

$ob^2+oa^2 = ab^2$

$ob^2+16^2 = 20^2$

ob = 12

Using pythagoras in triangle oam we get

am = $\sqrt {2^2 + 16^2 } $ = $\sqrt {260}$.

Question 10: In triangle DEF shown below, points A, B and C are taken on DE, DF and EF respectively such that EC = AC and CF = BC. If angle D equals 40 degress , then angle ACB is ?

a) 140

b) 70

c) 100

d) None of these

10) Answer (C)

View Video Solution

Solution:

Let angle EAC = x, so angle AEC = x and angle ACE = 180-2x
Let angle FBC = y, so angle BFC = y and angle BCF = 180-2y
So, angle ACB = 180-(180-2x+180-2y) = 2(x+y) – 180
x+y = 180 – 40 = 140
So, angle ACB = 280 – 180 = 100

Enroll to CAT 2023 Online Coaching

Download CAT Quant Formulas PDF