How to solve data sufficiency questions in CAT:
Data Sufficiency is one of the key areas in CAT and one expect at least 5 questions on it. Data Sufficiency questions always have two statements and these four options in CAT:
A) Both statements together are sufficient to answer the question
B) Only one of the statements alone is sufficient to answer the question but not the other.
C) Each of the statements alone can answer the question
D) Both the statements together are not sufficient to answer the question.
Given it’s high weightage and frequency of showing up in the exam, it is certainly a good idea to practice them well and make oneself familiar with all the types of Data Sufficiency questions for CAT. Here are 4 tips to solve those questions:
Don’t be in a rush to solve the question till the final answer.
Unlike other formats of questions, DS doesn’t require that you solve the question and obtain the answer. You just have to determine if the statements are sufficient to answer the question. You won’t get any additional marks for solving till the end. For example consider this question:
Question: What is the value of x and y?
Statement 1: x = 7y + 6
Statement 2: 5x – 35y = 22
Here we can rearrange the second statement to obtain x = 7y + 4.4
Both the statements are, therefore, not consistent. Observe that we are not trying to calculate the final values of x and y. That will be a waste of time. As soon as we realize that we can’t obtain the values of x and y using both the statements, we choose answer (D).
Cracku is offering Practice problems for CAT Data Sufficiency including solutions.
Use the process of elimination.
If required, you can randomly select an answer from the remaining ones after eliminating some options. Eliminating a couple of options greatly increases the probability of getting the answer right. Let’s consider an example:
Question: How old will Jagan be on Jan 1st 2015?
Statement 1: Jagan is two years younger than Lokesh and both their ages are prime numbers on Jan 1st 2013.
Statement 2: Jagan’s age was a prime number on Jan 1st 2011.
The question can’t be answered by using only one of the two Statements given. We can thus eliminate (B) and (C) even before doing the rest of the calculations, we can conclude the answer is either (A) or (D).
Using both the statements together, if Jagan is aged x in 2013, we can conclude that x-2, x and x+2 are prime.
This is true only for the set {3, 5, 7}.
So, x is 5 and Jagan will be aged 7 on Jan 1st 2015.
Hence, the question can be answered using both the statements together (A). Cracku offers FREE daily tests for CAT which are very useful for regular practice.
Don’t assume things that aren’t mentioned.
Often candidates assume that all numbers are positive, or that a chord is the diameter of a circle, etc. That will lead to wrong answers. Silly mistakes like these have double costs on the performance of the student. Firstly, there are negative marks for wrong answers. Secondly, lots of precious time gets wasted on wrong calculations.
Data Sufficiency Questions PDF
Are the two triangles ABC and PQR similar to each other?Practice from previous CAT question papers  to sharpen your Data Sufficiency skills. To illustrate the example, lets consider the following question:
Statement 1: AB = PQ and BC = RQ
Statement 2: angle B = angle P = 90 degrees
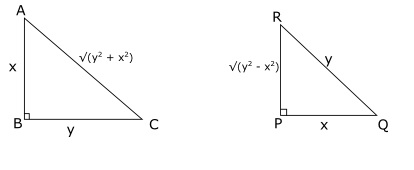
Let AB = x and BC = y. From statements 1 and 2, we know that PQ = x and QR = y => AC = $\sqrt{x^2+y^2}$ and PR = $\sqrt{y^2 – x^2}$.
If we rule out the case that $x/\sqrt{y^2 – x^2}$ = $y/x$, then we can say that the triangles are not similar.
=> $x^2$ = $y*\sqrt{y^2 – x^2}$. If we let x = 1, then solving the equation gives y = $\sqrt{½(1+\sqrt5)}$. So, the case that the triangles are similar is not impossible. Therefore, we cannot answer the question even by using both the statements together.
Had we assumed that triangles were similar even before solving the question, we would have lost marks in this question.
Keep note of time
. Data Sufficiency questions tend to be extremely time consuming at times. It is important to work fast and zero in on the correct option or just pass it. Take an example of a lengthy question:
The average weight of a class of 100 students is 45 kg. The class consists of two sections, I and II, each with 50 students. The average weight, $W_I$ , of Section I is smaller than the average weight, $W_{II}$ , of Section II. If the heaviest student, say Deepak, of Section II is moved to Section I, and the lightest student, say Poonam, of Section I is moved to Section II, then the average weights of the two sections are switched, i.e., the average weight of Section I becomes $W_{II}$ and that of Section II becomes $W_I$ . What is the weight of Poonam?
Statement 1: $W_{II} – W_I = 1.0 $
Statement 2: Moving Deepak from Section II to I (without any move from I to II) makes the average weights of the two sections equal.
Let w1 and w2 be average of both the groups respectively.
Since average of whole class is 45. $\frac{50*w1+50*w2}{100} = 45 $ => w1 + w2 = 90
And if we consider Statement 1, we have w2-w1 = 1. From the two equations average weight can be found out.
Further using the equations deduced from given condition which are : $\frac{50*w1-l+h}{50} = w2$ and $\frac{50*w2+l-h}{50} = w1$ where l and h is weight of Poonam and Deepak respectively. Hence we can find out weight of Poonam using statement 1.
If we consider Statement 2, since only Deepak is transferred we can’t find Poonam’s weight which will still be unknown. Hence Statement 1 is enough to know Poonam’s weight.
This question can take upto 5 mins to answer and is well left if there is a time crunch. Use Cracku CAT percentile predictor to accurately assess your chances of being qualified to top IIMs.
