CAT Averages Questions PDF [ Most Important Questions]

Averages is one of the most important topics in the Quantitative Ability section of CAT. It is an easy topic and so one must not avoid this topic. You can check out these Averages CAT Previous year questions. Practice a good number of questions on CAT Averages questions. In this article, we will look into some important Averages Questions for CAT. These are a good source for practice; If you want to practice these questions, you can download this CAT Averages Questions PDF below, which is completely Free.

Download Average Questions for CAT

Enroll for CAT 2022 Online Course

Question 1: Consider a sequence of seven consecutive integers. The average of the first five integers is n. The average of all the seven integers is:
[CAT 2000]

a) n

b) n+1

c) kn, where k is a function of n

d) n+(2/7)

1) Answer (B)

View Video Solution

Solution:

The first five numbers could be n-2, n-1, n, n+1, n+2. The next two number would then be, n+3 and n+4, in which case, the average of all the 7 numbers would be $\frac{(5n+2n+7)}{7}$ = n+1

Question 2: The average marks of a student in 10 papers are 80. If the highest and the lowest scores are not considered, the average is 81. If his highest score is 92, find the lowest.

a) 55

b) 60

c) 62

d) Cannot be determined

2) Answer (B)

View Video Solution

Solution:

Total marks = 80 x 10 = 800
Total marks except highest and lowest marks = 81 x 8 = 648
So Summation of highest marks and lowest marks will be = 800 – 648 = 152
When highest marks is 92, lowest marks will be = 152-92 = 60

Question 3: Total expenses of a boarding house are partly fixed and partly varying linearly with the number of boarders. The average expense per boarder is Rs. 700 when there are 25 boarders and Rs. 600 when there are 50 boarders. What is the average expense per boarder when there are 100 boarders?

a) 550

b) 580

c) 540

d) 560

3) Answer (A)

View Video Solution

Solution:

Let the fixed income be x and the number of boarders be y.

x + 25y = 17500

x + 50y = 30000

=> y = 500 and x = 5000

x + 100y = 5000 + 50000 = 55000

Average expense = $\frac{55000}{100}$ = Rs.550.

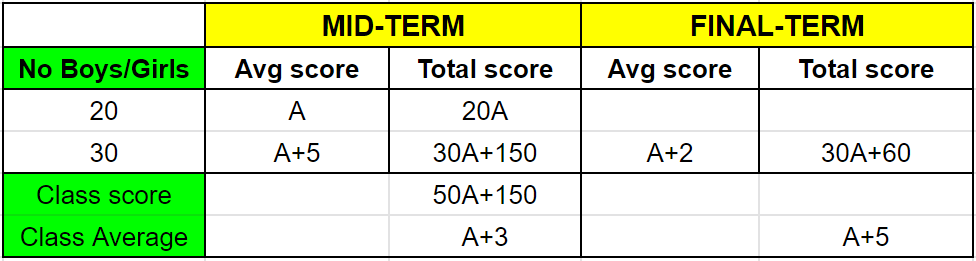
Question 4: A class consists of 20 boys and 30 girls. In the mid-semester examination, the average score of the girls was 5 higher than that of the boys. In the final exam, however, the average score of the girls dropped by 3 while the average score of the entire class increased by 2. The increase in the average score of the boys is

a) 9.5

b) 10

c) 4.5

d) 6

4) Answer (A)

View Video Solution

Solution:

Let, the average score of boys in the mid semester exam is A.
Therefore, the average score of girls in the mid semester exam be A+5.
Hence, the total marks scored by the class is $20\times (A) + 30\times (A+5) = 50\times A + 150$

The average score of the entire class is $\dfrac{(50\times A + 150)}{50} = A + 3$

wkt, class average increased by 2, class average in final term $= (A+3) + 2 = A + 5$

Given, that score of girls dropped by 3, i.e $(A+5)-3 = A+2$
Total score of girls in final term $= 30\times(A+2) = 30A + 60$

Total class score in final term $= (A + 5)\times50 = 50A + 250$

the total marks scored by the boys is $(50A + 250) – (30A – 60) = 20A + 190$
Hence, the average of the boys in the final exam is $\dfrac{(20G + 190)}{20} = A + 9.5$

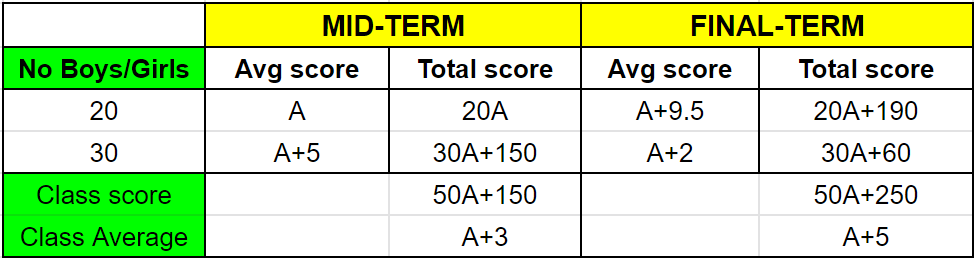
Hence, the increase in the average marks of the boys is $(A+9.5) – A = 9.5$

Question 5: The average height of 22 toddlers increases by 2 inches when two of them leave this group. If the average height of these two toddlers is one-third the average height of the original 22, then the average height, in inches, of the remaining 20 toddlers is

a) 30

b) 28

c) 32

d) 26

5) Answer (C)

View Video Solution

Solution:

Let the average height of 22 toddlers be 3x.
Sum of the height of 22 toddlers = 66x
Hence average height of the two toddlers who left the group = x
Sum of the height of the remaining 20 toddlers = 66x – 2x = 64x
Average height of the remaining 20 toddlers = 64x/20 = 3.2x
Difference = 0.2x = 2 inches => x = 10 inches
Hence average height of the remaining 20 toddlers = 3.2x = 32 inches

Checkout: CAT Free Practice Questions and Videos

Question 6: In an apartment complex, the number of people aged 51 years and above is 30 and there are at most 39 people whose ages are below 51 years. The average age of all the people in the apartment complex is 38 years. What is the largest possible average age, in years, of the people whose ages are below 51 years?

a) 27

b) 25

c) 26

d) 28

6) Answer (D)

View Video Solution

Solution:

The possible average age of people whose ages are below 51 years will be maximum if the average age of the number of people aged 51 years and above is minimum. Hence, we can say that that there are 30 people having same age 51 years.

Let ‘x’ be the maximum average age of people whose ages are below 51.

Then we can say that,

$\dfrac{51*30+39*x}{30+39} = 38$

$\Rightarrow$ $1530+39x = 2622$

$\Rightarrow$ $x = 1092/39 = 28$

Hence, we can say that option D is the correct answer.

Question 7: A CAT aspirant appears for a certain number of tests. His average score increases by 1 if the first 10 tests are not considered, and decreases by 1 if the last 10 tests are not considered. If his average scores for the first 10 and the last 10 tests are 20 and 30, respectively, then the total number of tests taken by him is

7) Answer: 60

View Video Solution

Solution:

Let the total number of tests be ‘n’ and the average by ‘A’
Total score = n*A
When 1st 10 tests are excluded, decrease in total value of scores = (nA – 20 * 10) = (nA – 200)
Also, (n – 10)(A + 1) = (nA – 200)
On solving, we get 10A – n = 190……….(i)
When last 10 tests are excluded, decrease in total value of scores = (nA – 30 * 10) = (nA – 300)
Also, (n – 10)(A – 1) = (nA – 300)
On solving, we get 10A + n = 310……….(ii)
From (i) and (ii), we get n = 60
Hence, 60 is the correct answer.

Question 8: Three classes X, Y and Z take an algebra test.
The average score in class X is 83.
The average score in class Y is 76.
The average score in class Z is 85.
The average score of all students in classes X and Y together is 79.
The average score of all students in classes Y and Z together is 81.
What is the average for all the three classes?

a) 81

b) 81.5

c) 82

d) 84.5

8) Answer (B)

View Video Solution

Solution:

Let x , y and z be no. of students in class X, Y ,Z respectively.

From 1st condition we have

83*x+76*y = 79*x+79*y which give 4x = 3y.

Next we have 76*y + 85*z = 81(y+z) which give 4z = 5y .

Now overall average of all the classes can be given as $\frac{83x+76y+85z}{x+y+z}$

Substitute the relations in above equation we get,

$\frac{83x+76y+85z}{x+y+z}$  = (83*3/4 + 76 + 85*5/4)/(3/4 + 1 + 5/4) = 978/12 = 81.5

Question 9: Ten years ago, the ages of the members of a joint family of eight people added up to 231 years. Three years later, one member died at the age of 60 years and a child was born during the same year. After another three years, one more member died, again at 60, and a child was born during the same year. The current average age of this eight-member joint family is nearest to
[CAT 2007]

a) 23 years

b) 22 years

c) 21 years

d) 25 years

e) 24 years

9) Answer (E)

View Video Solution

Solution:

Ten years ago, the total age of the family is 231 years.

Seven years ago, (Just before the death of the first person), the total age of the family would have been 231+8*3 = 231+24 = 255.
This is because, in 3 years, every person in the family would have aged by 3 years,
Total change in age = 231+24 = 255

After the death of one member, the total age is 255-60 = 195 years.

Since a child takes birth in the same year, the number of members remain the same i.e. (7+1) = 8

Four years ago, (i.e. 6 years after start date) one of the member of age 60 dies,
therefore, total age of the family is 195+24-60 = 159 years.

Since a child takes birth in the same year, the number of members remain the same i.e. (7+1) = 8

After 4 more years, the current total age of the family is = 8×4 + 159 = 191 years

The average age is 191/8 = 23.875 years = 24 years (approx)

Alternatively,
Since the number of members is always the same throughout
The 2 older members dropped their age by 60
So, after 10yrs, total age = 231 + 8*10 – 2*60 = 191
Average age = 191/8 = 23.875 $\simeq$ 24

Question 10: Consider the set S = {2, 3, 4, …., 2n+1}, where n is a positive integer larger than 2007. Define X as the average of the odd integers in S and Y as the average of the even integers in S. What is the value of X – Y ?

a) 0

b) 1

c) (1/2)*n

d) (n+1)/2n

e) 2008

10) Answer (B)

View Video Solution

Solution:

The odd numbers in the set are 3, 5, 7, …2n+1

Sum of the odd numbers = 3+5+7+…+(2n+1) = $n^2 + 2n$

Average of odd numbers = $n^2 + 2n$/n = n+2

Sum of even numbers = 2 + 4 + 6 + … + 2n = 2(1+2+3+…+n) = 2*n*(n+1)/2 = n(n+1)

Average of even numbers = n(n+1)/n = n+1

So, difference between the averages of even and odd numbers = 1