Arrangements is an important topic in the CAT LRDI section. These questions are not very tough; make sure you solve more CAT Arrangements questions. You can check out these CAT Arrangements questions from the CAT Previous year papers. Practice a good number of sums in the CAT Arrangements so that you can answer these questions with ease in the exam. In this post, we will look into some important Arrangements Questions for CAT quants. These are a good source of practice for CAT 2022 preparation; If you want to practice these questions, you can download these Important Arrangements Questions for CAT (with detailed answers) PDF along with the video solutions below, which are completely Free.
Download Arrangements Questions for CAT
Enroll for CAT 2022 Online Course
Instructions
A shopping mall has a large basement parking lot with parking slots painted in it along a single row. These slots are quite narrow; a compact car can fit in a single slot but an SUV requires two slots. When a car arrives, the parking attendant guides the car to the first available slot from the beginning of the row into which the car can fit.
For our purpose, cars are numbered according to the order in which they arrive at the lot. For example, the first car to arrive is given a number 1, the second a number 2, and so on. This numbering does not indicate whether a car is a compact or an SUV. The configuration of a parking lot is a sequence of the car numbers in each slot. Each single vacant slot is represented by letter V.
For instance, suppose cars numbered 1 through 5 arrive and park, where cars 1, 3 and 5 are compact cars and 2 and 4 are SUVs. At this point, the parking lot would be described by the sequence 1, 2, 3, 4, 5. If cars 2 and 5 now vacate their slots, the parking lot would now be described as 1, V, V, 3, 4. If a compact car (numbered 6) arrives subsequently followed by an SUV (numbered 7), the parking lot would be described by the sequence 1, 6, V, 3, 4, 7.
Answer the following questions INDEPENDENTLY of each other.
Question 1: Suppose that car 4 is not the first car to leave and that the sequence at a time between the arrival of the car 7 and car 8 is V, 7, 3, 6, 5. Then which of the following statements MUST be false?
a) Car 2 is a compact.
b) Car 7 is a compact.
c) Car 4 is an SUV.
d) Car 6 is a compact.
1) Answer (D)
Solution:
Here we can see that cars 3 and 5 are still in their position. Thus car 4 was not the first car to leave, either 1 or 2 left before 4. Let’s say only car 2 left before car 4. Now supposingly if car 2 is an SUV, car 6 was parked in that lot. Thus car 2 and car 7 are compact cars. Option 4 is correct.
Question 2: Suppose the sequence at some point of time is 4, 5, 6, V, 3. Which of the following is NOT necessarily true?
a) Car 4 is a compact.
b) Car 1 is an SUV.
c) Car 3 is an SUV
d) Car 5 is a compact.
2) Answer (C)
Solution:
The original sequence as given in the question is 4,5,6,V,3
This is possible when cars 1,2,3 arrived and then cars 1 and 2 leave. After that cars 4,5 and 6 arrive.
Now there are 4 slots to the left of car 3. This is only possible when cars 1 and 2 were SUVs. Now out of these 4 slots,
3 slots are occupied by cars 4,5 and 6. As a result these are compact cars . Car 3 can be a SUV or a Compact car and it won’t impact the final solution.
Question 3: Suppose eight cars have arrived, of which two have left. Also suppose that car 4 is a compact and car 7 is an SUV. Which of the following is a POSSIBLE current configuration of the parking lot?
a) 8, 2, 3, V, 6, 5, 7
b) V, 2, 3, 7, 5, 6, 8
c) 8, 2, 3, V, 5, 7, 6
d) 8, 2, 3, V, 5, 6, 7
3) Answer (D)
Solution:
Let’s look at option 4.
Order of cars is 8,2,3,V,5,6,7. This sequence is easily possible.
Let’s say cars 1,2,3,4,5,6,7 arrive one after the another.
Now Car 1 leaves and Car 8 takes that place.
Finally Car 4 leaves. Hence we can see that this combination of cars is possible
Question 4: Initially cars numbered 1, 2, 3, and 4 arrive among which 1 and 4 are SUVs while 2 and 3 are compact cars. Car 1 then leaves, followed by the arrivals of car 5 (a compact car) and car 6 (an SUV). Car 4 then leaves. Then car 7 (an SUV) and car 8 (a compact car) arrive. At this moment, which among the following numbered car is parked next to car 3?
a) 8
b) 5
c) 6
d) 7
4) Answer (D)
Solution:
following is the order of arrival and departure of cars
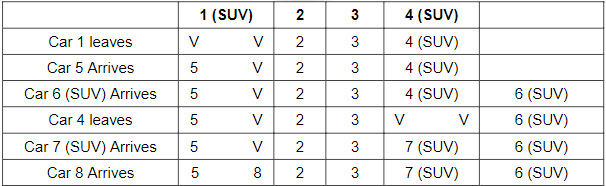
As we can see that car 2 and car 7 are parked next to car 3
Instructions
Twenty five coloured beads are to be arranged in a grid comprising of five rows and five columns. Each cell in the grid must contain exactly one bead. Each bead is coloured either Red, Blue or Green. While arranging the beads along any of the five rows or along any of the five columns, the rules given below are to be followed:
1. Two adjacent beads along the same row or column are always of different colours.
2. There is at least one Green bead between any two Blue beads along the same row or column.
3. There is at least one Blue and at least one Green bead between any two Red beads along the same row or column.
Every unique, complete arrangement of twenty five beads is called a configuration.
Question 5: Two Red beads have been placed in ‘second row, third column’ and ‘third row, second column’. How many more Red beads can be placed so as to maximise the number of Red beads used in the configuration?
5) Answer: 6
Solution:
6 more beads can be placed as shown

Checkout: CAT Free Practice Questions and Videos
Question 6: What is the minimum number of Blue beads in any configuration?
6) Answer: 6
Solution:
To solve this question we can use the answer of the previous question, since maximum 9 red beads are possible, filling the remaining space with green and blue beads, in such a way that number of blue beads is minimised

Hence number of blue beads is 6
Question 7: What is the maximum possible number of Red beads that can appear in any configuration?
7) Answer: 9
Solution:
Maximum 9 red beads are possible as shown here
Question 8: The total number of possible configurations using beads of only two colours is:
8) Answer: 2
Solution:

There are only 2 configurations possible

Instructions
Princess, Queen, Rani and Samragni were the four finalists in a dance competition. Ashman, Badal, Gagan and Dyu were the four music composers who individually assigned items to the dancers. Each dancer had to individually perform in two dance items assigned by the different composers. The first items performed by the four dancers were all assigned by different music composers. No dancer performed her second item before the performance of the first item by any other dancers. The dancers performed their second items in the same sequence of their performance of their first items.
The following additional facts are known.
i) No composer who assigned item to Princess, assigned any item to Queen.
ii) No composer who assigned item to Rani, assigned any item to Samragni.
iii) The first performance was by Princess; this item was assigned by Badal.
iv) The last performance was by Rani; this item was assigned by Gagan.
v) The items assigned by Ashman were performed consecutively. The number of performances between items assigned by each of the remaining composers was the same.
Question 9: Which pair of performances were composed by the same composer?
a) The first and the seventh
b) The third and the seventh
c) The second and the sixth
d) The first and the sixth
9) Answer (D)
Solution:

Since the dancers performed their second items in the same sequence of their performance of their first items. The table will be as follows:

The items assigned by Ashman were performed consecutively. The number of performances between items assigned by each of the remaining composers was the same.
Also, the first items performed by the four dancers were all assigned by different music composers. Badal can come only at the place as shown in the table.

Then Ashman can only compose for the following performances.

Hence Dyu will compose for the following performances:

From (i) No composer who assigned item to Princess, assigned any item to Queen.
From (ii) No composer who assigned item to Rani, assigned any item to Samragni.
Hence Dyu will compose for Samragni 1st Performance and Gagan will compose for Queen 1st Performance. Also, Badal will compose for Samragni 2nd Performance and Dyu will compose for Queens 2nd Performance.
Hence, the complete table is as follows:

The first and the sixth items were composed by Badal. Hence D is the answer.
Question 10: The sixth performance was composed by:
a) Badal
b) Dyu
c) Ashman
d) Gagan
10) Answer (A)
Solution:

Since the dancers performed their second items in the same sequence of their performance of their first items. The table will be as follows:

The items assigned by Ashman were performed consecutively. The number of performances between items assigned by each of the remaining composers was the same.
Also, the first items performed by the four dancers were all assigned by different music composers. Badal can come only at the place as shown in the table.

Then Ashman can only compose for the following performances.

Hence Dyu will compose for the following performances:

From (i) No composer who assigned item to Princess, assigned any item to Queen.
From (ii) No composer who assigned item to Rani, assigned any item to Samragni.
Hence Dyu will compose for Samragni 1st Performance and Gagan will compose for Queen 1st Performance. Also, Badal will compose for Samragni 2nd Performance and Dyu will compose for Queens 2nd Performance.
Hence, the complete table is as follows:

The sixth performance was composed by Badal. Hence C is the answer.
Question 11: Which of the following is FALSE?
a) Samragni did not perform in any item composed by Ashman.
b) Princess did not perform in any item composed by Dyu.
c) Rani did not perform in any item composed by Badal.
d) Queen did not perform in any item composed by Gagan.
11) Answer (D)
Solution:

Since the dancers performed their second items in the same sequence of their performance of their first items. The table will be as follows:

The items assigned by Ashman were performed consecutively. The number of performances between items assigned by each of the remaining composers was the same.
Also, the first items performed by the four dancers were all assigned by different music composers. Badal can come only at the place as shown in the table.

Then Ashman can only compose for the following performances.

Hence Dyu will compose for the following performances:

From (i) No composer who assigned item to Princess, assigned any item to Queen.
From (ii) No composer who assigned item to Rani, assigned any item to Samragni.
Hence Dyu will compose for Samragni 1st Performance and Gagan will compose for Queen 1st Performance. Also, Badal will compose for Samragni 2nd Performance and Dyu will compose for Queens 2nd Performance.
Hence, the complete table is as follows:

Option A: Samragni did not perform in any item composed by Ashman. This statement is true.
Option B: Princess did not perform in any item composed by Dyu. This is also true.
Option C: Rani did not perform in any item composed by Badal. This statement is true.
Option D: Queen did not perform in any item composed by Gagan. This statement is false.
Hence D is the answer.
Question 12: Which of the following is true?
a) The second performance was composed by Dyu.
b) The third performance was composed by Dyu.
c) The third performance was composed by Ashman.
d) The second performance was composed by Gagan.
12) Answer (A)
Solution:

Since the dancers performed their second items in the same sequence of their performance of their first items. The table will be as follows:

The items assigned by Ashman were performed consecutively. The number of performances between items assigned by each of the remaining composers was the same.
Also, the first items performed by the four dancers were all assigned by different music composers. Badal can come only at the place as shown in the table.

Then Ashman can only compose for the following performances.

Hence Dyu will compose for the following performances:

From (i) No composer who assigned item to Princess, assigned any item to Queen.
From (ii) No composer who assigned item to Rani, assigned any item to Samragni.
Hence Dyu will compose for Samragni 1st Performance and Gagan will compose for Queen 1st Performance. Also, Badal will compose for Samragni 2nd Performance and Dyu will compose for Queens 2nd Performance.
Hence, the complete table is as follows:

The second performance was composed by Dyu. Hence A is the answer.
Instructions
A supermarket has to place 12 items (coded A to L) in shelves numbered 1 to 16. Five of these items are types of biscuits, three are types of candies and the rest are types of savouries. Only one item can be kept in a shelf. Items are to be placed such that all items of same type are clustered together with no empty shelf between items of the same type and at least one empty shelf between two different types of items. At most two empty shelves can have consecutive numbers.
The following additional facts are known.
1. A and B are to be placed in consecutively numbered shelves in increasing order.
2. I and J are to be placed in consecutively numbered shelves both higher numbered than the shelves in which A and B are kept.
3. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies.
4. K is to be placed in shelf number 16.
5. L and J are items of the same type, while H is an item of a different type.
6. C is a candy and is to be placed in a shelf preceded by two empty shelves.
7. L is to be placed in a shelf preceded by exactly one empty shelf.
Question 13: Which of the following statements is necessarily true?
a) All biscuits are kept before candies.
b) There are two empty shelves between the biscuits and the candies.
c) All candies are kept before biscuits.
d) There are at least four shelves between items B and C.
13) Answer (D)
Solution:
The total number of biscuits = 5, the total number of candies =3 and the total number of savouries = 12-(3+5)=4
Representing the candies as C, biscuits as B and savories as S. K is to be placed in shelf number 16. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies. Since there is no empty shelf between the items of same type, D,E,F and K are savouries and placed at 13,14,15 and 16 respectively. This can be tabulated as follows:

The shelf 12 will be empty.
It is given that items are to be placed such that all items of same type are clustered together.
From 1, A and B are to be placed in consecutively numbered shelves in increasing order.
From 6, C is a candy and is to be placed in a shelf preceded by two empty shelves and from 7, L is to be placed in a shelf preceded by exactly one empty shelf.
Hence C and L are items of different types. Since C is a candy, L will be a biscuit.
From 5, L and J are items of the same type, while H is an item of a different type.
Since I and J are clustered together, I, J and L are biscuits and H is a candy.
So C,H are candies and I,J,L are biscuits. It is given that A, B are place consecutively. Hence A and B are items of same types. So A, B should be biscuits because if they are candies, there will be 4 candies.
Hence, I,J,L,A,B are biscuits and C,H and G are candies.
Now there are two empty shelves before C and exactly one empty shelf before L, then the different cases can be tabulated as follows:
Case 1:

Case 2:

Option A and C are wrong as candies can come before biscuits and vice versa. B is not necessarily true as there can be one empty shelf too as shown in the table. Option D is true as there are at least 4 shelves between B and C. Hence D is the answer.
Question 14: Which of the following can represent the numbers of the empty shelves in a possible arrangement?
a) 1, 7, 11, 12
b) 1, 5, 6, 12
c) 1, 2, 6, 12
d) 1, 2, 8, 12
14) Answer (C)
Solution:
The total number of biscuits = 5, the total number of candies =3 and the total number of savouries = 12-(3+5)=4
Representing the candies as C, biscuits as B and savories as S. K is to be placed in shelf number 16. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies. Since there is no empty shelf between the items of same type, D,E,F and K are savouries and placed at 13,14,15 and 16 respectively. This can be tabulated as follows:

The shelf 12 will be empty.
It is given that items are to be placed such that all items of same type are clustered together.
From 1, A and B are to be placed in consecutively numbered shelves in increasing order.
From 6, C is a candy and is to be placed in a shelf preceded by two empty shelves and from 7, L is to be placed in a shelf preceded by exactly one empty shelf.
Hence C and L are items of different types. Since C is a candy, L will be a biscuit.
From 5, L and J are items of the same type, while H is an item of a different type.
Since I and J are clustered together, I, J and L are biscuits and H is a candy.
So C,H are candies and I,J,L are biscuits. It is given that A, B are place consecutively. Hence A and B are items of same types. So A, B should be biscuits because if they are candies, there will be 4 candies.
Hence, I,J,L,A,B are biscuits and C,H and G are candies.
Now there are two empty shelves before C and exactly one empty shelf before L, then the different cases can be tabulated as follows:
Case 1:

Case 2:

From the table(case 2), only 1,2,6 and 12 are empty in the same arrangement. Hence, C is the answer.
Question 15: Which of the following items is not a type of biscuit?
a) L
b) A
c) B
d) G
15) Answer (D)
Solution:
The total number of biscuits = 5, the total number of candies =3 and the total number of savouries = 12-(3+5)=4
Representing the candies as C, biscuits as B and savories as S. K is to be placed in shelf number 16. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies. Since there is no empty shelf between the items of same type, D,E,F and K are savouries and placed at 13,14,15 and 16 respectively. This can be tabulated as follows:

The shelf 12 will be empty.
It is given that items are to be placed such that all items of same type are clustered together.
From 1, A and B are to be placed in consecutively numbered shelves in increasing order.
From 6, C is a candy and is to be placed in a shelf preceded by two empty shelves and from 7, L is to be placed in a shelf preceded by exactly one empty shelf.
Hence C and L are items of different types. Since C is a candy, L will be a biscuit.
From 5, L and J are items of the same type, while H is an item of a different type.
Since I and J are clustered together, I, J and L are biscuits and H is a candy.
So C,H are candies and I,J,L are biscuits. It is given that A, B are place consecutively. Hence A and B are items of same types. So A, B should be biscuits because if they are candies, there will be 4 candies.
Hence, I,J,L,A,B are biscuits and C,H and G are candies.
Now there are two empty shelves before C and exactly one empty shelf before L, then the different cases can be tabulated as follows:
Case 1:

Case 2:

G is a candy. Hence D is the answer.
Question 16: In how many different ways can the items be arranged on the shelves?
a) 8
b) 4
c) 2
d) 1
16) Answer (A)
Solution:
The total number of biscuits = 5, the total number of candies =3 and the total number of savouries = 12-(3+5)=4
Representing the candies as C, biscuits as B and savories as S. K is to be placed in shelf number 16. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies. Since there is no empty shelf between the items of same type, D,E,F and K are savouries and placed at 13,14,15 and 16 respectively. This can be tabulated as follows:

The shelf 12 will be empty.
It is given that items are to be placed such that all items of same type are clustered together.
From 1, A and B are to be placed in consecutively numbered shelves in increasing order.
From 6, C is a candy and is to be placed in a shelf preceded by two empty shelves and from 7, L is to be placed in a shelf preceded by exactly one empty shelf.
Hence C and L are items of different types. Since C is a candy, L will be a biscuit.
From 5, L and J are items of the same type, while H is an item of a different type.
Since I and J are clustered together, I, J and L are biscuits and H is a candy.
So C,H are candies and I,J,L are biscuits. It is given that A, B are place consecutively. Hence A and B are items of same types. So A, B should be biscuits because if they are candies, there will be 4 candies.
Hence, I,J,L,A,B are biscuits and C,H and G are candies.
Now there are two empty shelves before C and exactly one empty shelf before L, then the different cases can be tabulated as follows:
Case 1:

Case 2:

The number of arrangements for the first case = 2*2=4
The number of arrangements for the second case = 2*2=4
The total number of arrangements = 4+4=8
Instructions
Direction : Answer the questions based on the information provided.
A group of students A,B, C, D, E, F, G, H and I visit Sheesh Mahal in Jaipur and play a game of standing in a horizontal line in front of a mirror as per the directions seen in the reflection. The group consists of four girls and five boys and none of the boys are at the extreme end positions. All the boys stand together with no girl in between. A takes the lead and stands in the centre to give directions as per those seen in the reflection. Some other directions which A gives are :
(a) Gis on the extreme left while A is to the immediate left of D.
(b) C stands two places to the right of A and is not a girl.
(c) H is second to the left of B and to the immediate right of G.
(d) E is not on the extreme ends and is not a girl.
(e) B always stands between two boys.
Question 17: If there are two students between F and D, then I as per reflection is :
a) On the extreme right
b) Immediate left of D
c) Immediate right of C
d) Four places to the right of A
17) Answer (C)
Solution:

From the diagram , we can infer that option C is the answer.
Question 18: Whois three placesto the right of A considering A’s direction sense and not that of the reflection ?
a) F
b) I
c) H
d) E
18) Answer (C)
Solution:

The answer is H.
Question 19: Which of the following statementis always true ?
a) F and I are girls
b) E is a boy but A is a girl
c) A and E stand together
d) C and I stand together
19) Answer (A)
Solution:

Option A is the correct answer
Instructions
Direction : Answer the questions based on the information provided.
In Gargi’s family there are 7 members A, B,C, D, E, F and G other than her consisting of Mother, Father, Brother, Sister, Uncle, Grandfather and Grandmother. They are Doctor, Professor, Director, Actor, Minister, Business Person and Artist by profession not necessarily in the same order. Gargi is a Manager of a leading restaurant and invites the family to her restaurant having round tables for seating to have dinner. The family members select a table for dinner while Gargi is on duty. Few other details are :
(a) The mother and father do not sit together.
(b) C is seated on the immediate left of Professor and A sits with B.
(c) The artist is either the sister or grandmother and sits to the immediate right of Father.
(d) The grandmother is seated on the immediate left of D who is an actor.
(e) G who is an artist sits with the Business person, F who is a female.
(f) E sits second to the left of Director.
(g) There is one family member between Grandmother and C who is a Director.
(h) Father is a doctor and sits between Professor and Sister.
(i) Brother is not a Professor and sits with Grandmother.
Question 20: Who sits three places to the right of Mother ?
a) Director
b) Uncle
c) Grandfather
d) Brother
20) Answer (A)
Solution:
After reading the sentences D,G,B, we get two cases with the following partially filled table

After filling in details with b and e we arrive at

Here, father/doctor has to sit between professor and sister. This is violated in first case. Hence, it is rejected.

The final arrangement is as given above. Director is the correct answer.
Question 21: If C is the Uncle, then Professor is :
a) Grandfather
b) A
c) B
d) Mother
21) Answer (A)
Solution:
After reading the sentences D,G,B, we get two cases with the following partially filled table

After filling in details with b and e we arrive at

Here, father/doctor has to sit between professor and sister. This is violated in first case. Hence, it is rejected.

The final arrangement is as given above. If C is uncle, then professor is grandfather.
Question 22: If B is a Doctor, then who is A ?
a) Father
b) Uncle
c) Professor
d) Mother
22) Answer (C)
Solution:
After reading the sentences D,G,B, we get two cases with the following partially filled table

After filling in details with b and e we arrive at

Here, father/doctor has to sit between professor and sister. This is violated in first case. Hence, it is rejected.

The final arrangement is as given above. If B is doctor, then A is professor.
Question 23: How many minimum/least number of people are between the Business person and Professor ?
a) 3
b) 2
c) 4
d) 1
23) Answer (B)
Solution:
After reading the sentences D,G,B, we get two cases with the following partially filled table

After filling in details with b and e we arrive at

Here, father/doctor has to sit between professor and sister. This is violated in first case. Hence, it is rejected.

The final arrangement is as given above. There are two persons between business person and professor.
Instructions
The first year students in a business school are split into six sections. In 2019 the Business Statistics course was taught in these six sections by Annie, Beti, Chetan, Dave, Esha, and Fakir. All six sections had a common midterm (MT) and a common endterm (ET) worth 100 marks each. ET contained more questions than MT. Questions for MT and ET were prepared collectively by the six faculty members. Considering MT and ET together, each faculty member prepared the same number of questions.
Each of MT and ET had at least four questions that were worth 5 marks, at least three questions that were worth 10 marks, and at least two questions that were worth 15 marks. In both MT and ET, all the 5-mark questions preceded the 10-mark questions, and all the 15- mark questions followed the 10-mark questions.
The following additional facts are known.
i. Annie prepared the fifth question for both MT and ET. For MT, this question carried 5 marks.
ii. Annie prepared one question for MT. Every other faculty member prepared more than one questions for MT.
iii. All questions prepared by a faculty member appeared consecutively in MT as well as ET.
iv. Chetan prepared the third question in both MT and ET; and Esha prepared the eighth question in both.
v. Fakir prepared the first question of MT and the last one in ET. Dave prepared the last question of MT and the first one in ET.
Question 24: Which of the following questions did Beti prepare in ET?
a) Seventh question
b) Fourth question
c) Ninth question
d) Tenth question
24) Answer (D)
Solution:
All six sections had a common midterm (MT) and a common end term (ET) worth 100 marks each.
Each of MT and ET had at least four questions that were worth 5 marks, at least three questions that were worth 10 marks, and at least two questions that were worth 15 marks.
5×4=20, 10×3=30, 15×2=30
The total possible with considering the minimum number of questions of each type = 20+30+30=80 marks.
Rest 20 marks are possible by the following cases: {5,5,5,5} {5,5,10} {10,10} {5,15}
ET contained more questions than MT.
Thus MT cannot consider the case {5,5,5,5}
The number of questions in each case:
1) {5,5,5,5} = 9+4 =13 questions
2) {5,5,10} = 9+3 =12 questions
3) {10,10} = 9+2 =11 questions
4) {5,15} = 9+2 =11 questions
Considering MT and ET together, each faculty member prepared the same number of questions. The total number of questions should be multiple of 6, thus the total number of questions will be 24.
For ET and MT, there are 2 cases :
{5,5,5,5}{5,15}
{5,5,5,5}{10,10}
According to the statement (i), Annie prepared the fifth question for both MT and ET. For MT, this question carried 5 marks. Thus {10,10} case is not possible.
MT {5,5,5,5,5,10,10,10,15,15,15}
ET {5,5,5,5,5,5,5,5,10,10,10,15,15}
From statement (i),(ii),(iv),(v), every other faculty member prepared two questions for MT.
we can create the following table:


{ Annie(A), Beti(B), Chetan(C), Dave (D), Fakir(F) }
There are 24 questions in total so each faculty will make 4 questions.
We can create the following table for ET.

Hence the correct option is D
Question 25: Who prepared 15-mark questions for MT and ET?
a) Only Beti, Dave, Esha and Fakir
b) Only Dave and Fakir
c) Only Esha and Fakir
d) Only Dave, Esha and Fakir
25) Answer (D)
Solution:
All six sections had a common midterm (MT) and a common end term (ET) worth 100 marks each.
Each of MT and ET had at least four questions that were worth 5 marks, at least three questions that were worth 10 marks, and at least two questions that were worth 15 marks.
5×4=20, 10×3=30, 15×2=30
The total possible with considering the minimum number of questions of each type = 20+30+30=80 marks.
Rest 20 marks are possible by the following cases: {5,5,5,5} {5,5,10} {10,10} {5,15}
ET contained more questions than MT.
Thus MT cannot consider the case {5,5,5,5}
The number of questions in each case:
1) {5,5,5,5} = 9+4 =13 questions
2) {5,5,10} = 9+3 =12 questions
3) {10,10} = 9+2 =11 questions
4) {5,15} = 9+2 =11 questions
Considering MT and ET together, each faculty member prepared the same number of questions. The total number of questions should be multiple of 6, thus the total number of questions will be 24.
For ET and MT, there are 2 cases :
{5,5,5,5}{5,15}
{5,5,5,5}{10,10}
According to the statement (i), Annie prepared the fifth question for both MT and ET. For MT, this question carried 5 marks. Thus {10,10} case is not possible.
MT {5,5,5,5,5,10,10,10,15,15,15}
ET {5,5,5,5,5,5,5,5,10,10,10,15,15}
From statement (i),(ii),(iv),(v), every other faculty member prepared two questions for MT.
we can create the following table:


{ Annie(A), Beti(B), Chetan(C), Dave (D), Fakir(F) }
There are 24 questions in total so each faculty will make 4 questions.
We can create the following table for ET.

Hence the correct option is D
Question 26: How many 5‐mark questions were there in MT and ET combined?
a) 13
b) 12
c) 10
d) Cannot be determined
26) Answer (A)
Solution:
All six sections had a common midterm (MT) and a common end term (ET) worth 100 marks each.
Each of MT and ET had at least four questions that were worth 5 marks, at least three questions that were worth 10 marks, and at least two questions that were worth 15 marks.
5×4=20, 10×3=30, 15×2=30
The total possible with considering the minimum number of questions of each type = 20+30+30=80 marks.
Rest 20 marks are possible by the following cases: {5,5,5,5} {5,5,10} {10,10} {5,15}
ET contained more questions than MT.
Thus MT cannot consider the case {5,5,5,5}
The number of questions in each case:
1) {5,5,5,5} = 9+4 =13 questions
2) {5,5,10} = 9+3 =12 questions
3) {10,10} = 9+2 =11 questions
4) {5,15} = 9+2 =11 questions
Considering MT and ET together, each faculty member prepared the same number of questions. The total number of questions should be multiple of 6, thus the total number of questions will be 24.
For ET and MT, there are 2 cases :
{5,5,5,5}{5,15}
{5,5,5,5}{10,10}
According to the statement (i), Annie prepared the fifth question for both MT and ET. For MT, this question carried 5 marks. Thus {10,10} case is not possible.
MT {5,5,5,5,5,10,10,10,15,15,15}
ET {5,5,5,5,5,5,5,5,10,10,10,15,15}
From statement (i),(ii),(iv),(v), every other faculty member prepared two questions for MT.
we can create the following table:


{ Annie(A), Beti(B), Chetan(C), Dave (D), Fakir(F) }
There are 24 questions in total so each faculty will make 4 questions.
We can create the following table for ET.

Hence the correct option is A
Question 27: The second question in ET was prepared by:
a) Chetan
b) Beti
c) Esha
d) Dave
27) Answer (D)
Solution:
All six sections had a common midterm (MT) and a common end term (ET) worth 100 marks each.
Each of MT and ET had at least four questions that were worth 5 marks, at least three questions that were worth 10 marks, and at least two questions that were worth 15 marks.
5×4=20, 10×3=30, 15×2=30
The total possible with considering the minimum number of questions of each type = 20+30+30=80 marks.
Rest 20 marks are possible by the following cases: {5,5,5,5} {5,5,10} {10,10} {5,15}
ET contained more questions than MT.
Thus MT cannot consider the case {5,5,5,5}
The number of questions in each case:
1) {5,5,5,5} = 9+4 =13 questions
2) {5,5,10} = 9+3 =12 questions
3) {10,10} = 9+2 =11 questions
4) {5,15} = 9+2 =11 questions
Considering MT and ET together, each faculty member prepared the same number of questions. The total number of questions should be multiple of 6, thus the total number of questions will be 24.
For ET and MT, there are 2 cases :
{5,5,5,5}{5,15}
{5,5,5,5}{10,10}
According to statement (i), Annie prepared the fifth question for both MT and ET. For MT, this question carried 5 marks. Thus {10,10} case is not possible.
MT {5,5,5,5,5,10,10,10,15,15,15}
ET {5,5,5,5,5,5,5,5,10,10,10,15,15}
From statement (i),(ii),(iv),(v), every other faculty member prepared two questions for MT.
we can create the following table:


{ Annie(A), Beti(B), Chetan(C), Dave (D), Fakir(F) }
There are 24 questions in total so each faculty will make 4 questions.
We can create the following table for ET.

Hence the correct option is D





