CAT 2020 LRDI Question Paper (Slot-2)

CAT 2020 LRDI Question Paper (Slot-2)
Download CAT 2020 LRDI Slot-2 Questions PDF with detailed solutions. Practice Data Interpretation and Logical Reasoning Slot-2 Questions asked in the CAT exam to understand the type and level of questions asked in the exam.

Download CAT 2020 LRDI Question Paper (Slot-2)

Take 3 Free CAT 2021 Mock Tests

Enroll to CAT 2021 online coaching

Instructions

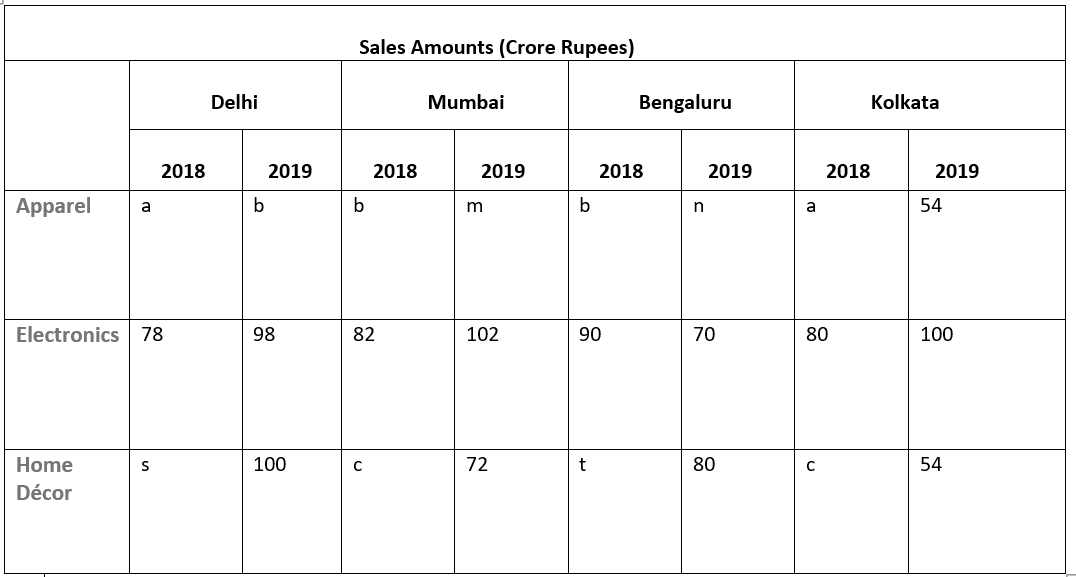
A chain of departmental stores has outlets in Delhi, Mumbai, Bengaluru and Kolkata. The sales are categorized by its three departments – ‘Apparel’, ‘Electronics’, and ‘Home Décor’. An Accountant has been asked to prepare a summary of the 2018 and 2019 sales amounts for an internal report. He has collated partial information and prepared the following table.

The following additional information is known.
1. The sales amounts in the Apparel departments were the same for Delhi and Kolkata in 2018.
2. The sales amounts in the Apparel departments were the same for Mumbai and Bengaluru in 2018. This sales amount matched the sales amount in the Apparel department for Delhi in 2019.
3. The sales amounts in the Home Décor departments were the same for Mumbai and Kolkata in 2018.
4. The sum of the sales amounts of four Electronics departments increased by the same amount as the sum of the sales amounts of four Apparel departments from 2018 to 2019.
5. The total sales amounts of the four Home Décor departments increased by Rs 70 Crores from 2018 to 2019.
6. The sales amounts in the Home Décor departments of Delhi and Bengaluru each increased by Rs 20 Crores from 2018 to 2019.
7. The sales amounts in the Apparel departments of Delhi and Bengaluru each increased by the same amount in 2019 from 2018. The sales amounts in the Apparel departments of Mumbai and Kolkata also each increased by the same amount in 2019 from 2018.
8. The sales amounts in the Apparel departments of Delhi, Kolkata and Bengaluru in 2019 followed an Arithmetic Progression.

Question 1: In Home Décor departments of which cities were the sales amounts the highest in 2018 and 2019, respectively?

a) Bengaluru and Delhi

b) Mumbai and Mumbai

c) Mumbai and Delhi

d) Delhi and Delhi

Question 2: What was the increase in sales amount, in Crore Rupees, in the Apparel department of Mumbai from 2018 to 2019?

a) 12

b) 8

c) 5

d) 10

Question 3: Among all the 12 departments (i.e., the 3 departments in each of the 4 cities), what was the maximum percentage increase in sales amount from 2018 to 2019?

a) 25

b) 28

c) 75

d) 50

Question 4: What was the total sales amount, in Crore Rupees, in 2019 for the chain of departmental stores?

a) 600

b) 900

c) 150

d) 750

Download Free MBA Preparation App
Instructions

In an election several candidates contested for a constituency. In any constituency, the winning candidate was the one who polled the highest number of votes, the first runner up was the one who polled the second highest number of votes, the second runner up was the one who polled the third highest number of votes, and so on. There were no ties (in terms of number of votes polled by the candidates) in any of the constituencies in this election. In an electoral system, a security deposit is the sum of money that a candidate is required to pay to the election commission before he or she is permitted to contest. Only the defeated candidates (i.e., one who is not the winning candidate) who fail to secure more than one sixth of the valid votes polled in the constituency, lose their security deposits.

The following table provides some incomplete information about votes polled in four constituencies: A, B, C and D, in this election .

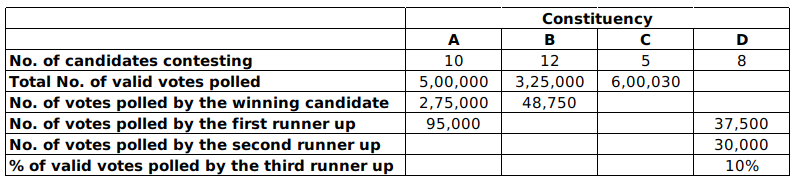
The following additional facts are known:

1. The first runner up polled 10,000 more votes than the second runner up in constituency A.
2. None of the candidates who contested in constituency C lost their security deposit. The difference in votes polled by any pair of candidates in this constituency was at least 10,000.
3. The winning candidate in constituency D polled 5% of valid votes more than that of the first runner up. All the candidates who lost their security deposits while contesting for this constituency, put together, polled 35% of the valid votes.

Question 5: What is the percentage of votes polled in total by all the candidates who lost their security deposits while contesting for constituency A?

Question 6: How many candidates who contested in constituency B lost their security deposit?

Question 7: What BEST can be concluded about the number of votes polled by the winning candidate in constituency C?

a) 1,40,010

b) between 1,40,005 and 1,40,010

c) less than 2,00,010

d) 1,40,006

Question 8: What was the number of valid votes polled in constituency D?

a) 1,25,000

b) 1,50,000

c) 1,75,000

d) 62,500

Question 9: The winning margin of a constituency is defined as the difference of votes polled by the winner and that of the first runner up. Which of the following CANNOT be the list of constituencies, in increasing order of winning margin?

a) D, B, C, A

b) B, D, C, A

c) B, C, D, A

d) D, C, B, A

Question 10: For all the four constituencies taken together, what was the approximate number of votes polled by all the candidates who lost their security deposit expressed as a percentage of the total valid votes from these four constituencies?

a) 38.25%

b) 23.54%

c) 23.91%

d) 32.00%

Enroll for CAT 2021 – Just Rs. 2700

Instructions

Twenty five coloured beads are to be arranged in a grid comprising of five rows and five columns. Each cell in the grid must contain exactly one bead. Each bead is coloured either Red, Blue or Green. While arranging the beads along any of the five rows or along any of the five columns, the rules given below are to be followed:

1. Two adjacent beads along the same row or column are always of different colours.
2. There is at least one Green bead between any two Blue beads along the same row or column.
3. There is at least one Blue and at least one Green bead between any two Red beads along the same row or column.

Every unique, complete arrangement of twenty five beads is called a configuration.

Question 11: The total number of possible configurations using beads of only two colours is:

Question 12: What is the maximum possible number of Red beads that can appear in any configuration?

Question 13: What is the minimum number of Blue beads in any configuration?

Question 14: Two Red beads have been placed in ‘second row, third column’ and ‘third row, second column’. How many more Red beads can be placed so as to maximise the number of Red beads used in the configuration?

Instructions

The Humanities department of a college is planning to organize eight seminars, one for each of the eight doctoral students – A, B, C, D, E, F, G and H. Four of them are from Economics, three from Sociology and one from Anthropology department. Each student is guided by one among P, Q, R, S and T. Two students are guided by each of P, R and T, while one student is guided by each of Q and S. Each student is guided by a guide belonging to their department. Each seminar is to be scheduled in one of four consecutive 30-minute slots starting at 9:00 am, 9:30 am, 10:00 am and 10:30 am on the same day. More than one seminars can be scheduled in a slot, provided the guide is free. Only three rooms are available and hence at the most three seminars can be scheduled in a slot. Students who are guided by the same guide must be scheduled in consecutive slots.

The following additional facts are also known.

1. Seminars by students from Economics are scheduled in each of the four slots.
2. A’s is the only seminar that is scheduled at 10:00 am. A is guided by R.
3. F is an Anthropology student whose seminar is scheduled at 10:30 am.
4. The seminar of a Sociology student is scheduled at 9:00 am.
5. B and G are both Sociology students, whose seminars are scheduled in the same slot. The seminar of an Economics student, who is guided by T, is also scheduled in the same slot.
6. P, who is guiding both B and C, has students scheduled in the first two slots.
7. A and G are scheduled in two consecutive slots.

Question 15: Which one of the following statements is true?

a) Two seminars are scheduled in the first slot.

b) Only one seminar is scheduled in the second slot.

c) Three seminars are scheduled in the first slot.

d) Three seminars are scheduled in the last slot.

Question 16: Who all are NOT guiding any Economics students?

a) Q, R and S

b) P, Q and R

c) P, R and S

d) P, Q and S

Question 17: Which of the following statements is necessarily true?

a) Q is guiding G.

b) H is an Economics student.

c) S is guiding F.

d) B is scheduled in the first slot.

Question 18: If D is scheduled in a slot later than Q’s, then which of the following two statement(s) is(are) true?
(i) E and H are guided by T.
(ii) G is guided by Q.

a) Only (ii)

b) Neither (i) nor (ii)

c) Only (i)

d) Both (i) and (ii)

Question 19: If E and Q are both scheduled in the same slot, then which of the following statements BEST describes the relationship between D, H, and T?

a) Exactly one of D and H is guided by T.

b) Both D and H are guided by T.

c) At least one of D and H is guided by T.

d) Neither D nor H is guided by T.

Question 20: If D is scheduled in the slot immediately before Q’s, then which of the following is NOT necessarily true?

a) G is guided by Q.

b) E is guided by R.

c) F is guided by S.

d) D is guided by T.

Join 7K MBA Aspirants Telegram Group

Instructions

A shopping mall has a large basement parking lot with parking slots painted in it along a single row. These slots are quite narrow; a compact car can fit in a single slot but an SUV requires two slots. When a car arrives, the parking attendant guides the car to the first available slot from the beginning of the row into which the car can fit.

For our purpose, cars are numbered according to the order in which they arrive at the lot. For example, the first car to arrive is given a number 1, the second a number 2, and so on. This numbering does not indicate whether a car is a compact or an SUV. The configuration of a parking lot is a sequence of the car numbers in each slot. Each single vacant slot is represented by letter V.

For instance, suppose cars numbered 1 through 5 arrive and park, where cars 1, 3 and 5 are compact cars and 2 and 4 are SUVs. At this point, the parking lot would be described by the sequence 1, 2, 3, 4, 5. If cars 2 and 5 now vacate their slots, the parking lot would now be described as 1, V, V, 3, 4. If a compact car (numbered 6) arrives subsequently followed by an SUV (numbered 7), the parking lot would be described by the sequence 1, 6, V, 3, 4, 7.

Answer the following questions INDEPENDENTLY of each other.

Question 21: Initially cars numbered 1, 2, 3, and 4 arrive among which 1 and 4 are SUVs while 2 and 3 are compact cars. Car 1 then leaves, followed by the arrivals of car 5 (a compact car) and car 6 (an SUV). Car 4 then leaves. Then car 7 (an SUV) and car 8 (a compact car) arrive. At this moment, which among the following numbered car is parked next to car 3?

a) 8

b) 5

c) 6

d) 7

Question 22: Suppose eight cars have arrived, of which two have left. Also suppose that car 4 is a compact and car 7 is an SUV. Which of the following is a POSSIBLE current configuration of the parking lot?

a) 8, 2, 3, V, 6, 5, 7

b) V, 2, 3, 7, 5, 6, 8

c) 8, 2, 3, V, 5, 7, 6

d) 8, 2, 3, V, 5, 6, 7

Question 23: Suppose the sequence at some point of time is 4, 5, 6, V, 3. Which of the following is NOT necessarily true?

a) Car 4 is a compact.

b) Car 1 is an SUV.

c) Car 3 is an SUV

d) Car 5 is a compact.

Question 24: Suppose that car 4 is not the first car to leave and that the sequence at a time between the arrival of the car 7 and car 8 is V, 7, 3, 6, 5. Then which of the following statements MUST be false?

a) Car 2 is a compact.

b) Car 7 is a compact.

c) Car 4 is an SUV.

d) Car 6 is a compact.

How to prepare for RC

How to prepare for PJ and Odd one out

Answers & Solutions:

1) Answer (D)

From 1, Let sales amounts in the Apparel departments for Delhi and Kolkata in 2018 be a.

From 2, Let sales amounts in the Apparel departments for Mumbai and Bengaluru in 2018 and for Delhi be b.

From 3, let the sales amounts in the Home Décor departments for Mumbai and Kolkata in 2018 be c and that of Delhi and Bengaluru be s and t respectively.

Let the Let sales amounts in the Apparel departments for Mumbai and Bengaluru in 2019 be m and n respectuvely.

The table looks like:

From 6, s=80 and t=60.
From 5, s+c+t+c+70=306 => 2c=96 => c=48.

From 4, (b-a)+(m-b)+(n-b)+(54-a)=(20)+20-20+20 => 54+m+n-2a-b=40=> 2a+b=14+m+n => 2b=28+2m+2n-4a…(i)

From 7, b-a=n-b => 2b=a+n…(ii) and m-b=54-a=> a+m=54+b=>2b=2a+2m-108…(iii)

From 8, 108=b+n=>2b=216-2n…(iv)

from (i) & (iii), 28+2m+2n-4a=2a+2m-108 => 6a=136+2n => 3a=68+n…(v)

from (ii) & (iv), 216-2n=a+n => a+3n=216=> 3a=648-9n…(vi)

from (v) & (vi), 648-9n=68+n => n=58 => a=42 => b=50 => m=62.

The final table looks like this

2) Answer (A)

From 1, Let sales amounts in the Apparel departments for Delhi and Kolkata in 2018 be a.

From 2, Let sales amounts in the Apparel departments for Mumbai and Bengaluru in 2018 and for Delhi be b.

From 3, let the sales amounts in the Home Décor departments for Mumbai and Kolkata in 2018 be c and that of Delhi and Bengaluru be s and t respectively.

Let the Let sales amounts in the Apparel departments for Mumbai and Bengaluru in 2019 be m and n respectuvely.

The table looks like:

From 6, s=80 and t=60.
From 5, s+c+t+c+70=306 => 2c=96 => c=48.

From 4, (b-a)+(m-b)+(n-b)+(54-a)=(20)+20-20+20 => 54+m+n-2a-b=40=> 2a+b=14+m+n => 2b=28+2m+2n-4a…(i)

From 7, b-a=n-b => 2b=a+n…(ii) and m-b=54-a=> a+m=54+b=>2b=2a+2m-108…(iii)

From 8, 108=b+n=>2b=216-2n…(iv)

from (i) & (iii), 28+2m+2n-4a=2a+2m-108 => 6a=136+2n => 3a=68+n…(v)

from (ii) & (iv), 216-2n=a+n => a+3n=216=> 3a=648-9n…(vi)

from (v) & (vi), 648-9n=68+n => n=58 => a=42 => b=50 => m=62.

The final table looks like this

Increase in sales =12

3) Answer (D)

From 1, Let sales amounts in the Apparel departments for Delhi and Kolkata in 2018 be a.

From 2, Let sales amounts in the Apparel departments for Mumbai and Bengaluru in 2018 and for Delhi be b.

From 3, let the sales amounts in the Home Décor departments for Mumbai and Kolkata in 2018 be c and that of Delhi and Bengaluru be s and t respectively.

Let the Let sales amounts in the Apparel departments for Mumbai and Bengaluru in 2019 be m and n respectuvely.

The table looks like:

From 6, s=80 and t=60.
From 5, s+c+t+c+70=306 => 2c=96 => c=48.

From 4, (b-a)+(m-b)+(n-b)+(54-a)=(20)+20-20+20 => 54+m+n-2a-b=40=> 2a+b=14+m+n => 2b=28+2m+2n-4a…(i)

From 7, b-a=n-b => 2b=a+n…(ii) and m-b=54-a=> a+m=54+b=>2b=2a+2m-108…(iii)

From 8, 108=b+n=>2b=216-2n…(iv)

from (i) & (iii), 28+2m+2n-4a=2a+2m-108 => 6a=136+2n => 3a=68+n…(v)

from (ii) & (iv), 216-2n=a+n => a+3n=216=> 3a=648-9n…(vi)

from (v) & (vi), 648-9n=68+n => n=58 => a=42 => b=50 => m=62.

The final table looks like this

Hence the percentage change is 50.

4) Answer (B)

From 1, Let sales amounts in the Apparel departments for Delhi and Kolkata in 2018 be a.

From 2, Let sales amounts in the Apparel departments for Mumbai and Bengaluru in 2018 and for Delhi be b.

From 3, let the sales amounts in the Home Décor departments for Mumbai and Kolkata in 2018 be c and that of Delhi and Bengaluru be s and t respectively.

Let the Let sales amounts in the Apparel departments for Mumbai and Bengaluru in 2019 be m and n respectively.

The table looks like:

From 6, s=80 and t=60.
From 5, s+c+t+c+70=306 => 2c=96 => c=48.

From 4, (b-a)+(m-b)+(n-b)+(54-a)=(20)+20-20+20 => 54+m+n-2a-b=40=> 2a+b=14+m+n => 2b=28+2m+2n-4a…(i)

From 7, b-a=n-b => 2b=a+n…(ii) and m-b=54-a=> a+m=54+b=>2b=2a+2m-108…(iii)

From 8, 108=b+n=>2b=216-2n…(iv)

from (i) & (iii), 28+2m+2n-4a=2a+2m-108 => 6a=136+2n => 3a=68+n…(v)

from (ii) & (iv), 216-2n=a+n => a+3n=216=> 3a=648-9n…(vi)

from (v) & (vi), 648-9n=68+n => n=58 => a=42 => b=50 => m=62.

The final table looks like this

.’. total sales amount, in Crore Rupees, in 2019 for the chain of departmental stores =900 cr.

Download CAT Previous Papers PDF

Take Free CAT Video Lectures

5) Answer: 9

It’s given in the question that the first runner up polled 10,000 more votes than the second runner up in constituency A. Now the first runner up has got 95000 votes, hence the second runner up will get 85000 votes.

Now the remaining votes will be 500000-275000-95000-85000=45000

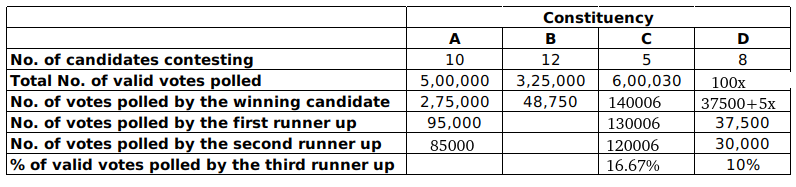
From 2, None of the candidates who contested in constituency C lost their security deposit. The difference in votes polled by any pair of candidates in this constituency was at least 10,000 => the person who got 5th highest votes must have got > 600030/6 => $\ge$ 100006. Since it is also given that the difference of votes is $\ge$ 10000, the only possible case is winner, 1st runner up, 2nd runner up, 3rd runner up, 4th runner up must have got 140006,130006,120006,110006,100006 respectively which sums upto exactly 600030.

Let the number of votes polled in D be 100x.

From 3, The winning candidate in constituency D must have got 15x+37500

The table now looks like:

Total votes in A = 500000 => the candidates who got $\le$ 83333 must have lost their security deposits => candidates till 2nd runner up didn’t lose their deposit =>all the candidates who received 500000-275000-95000-85000=45000 lost their deposits.

The percentage of votes polled in total by all the candidates who lost their security deposits while contesting for constituency A = 45000*100/500000 =9%

6) Answer: 11

It’s given in the question that the first runner up polled 10,000
more votes than the second runner up in constituency A. Now the first
runner up has got 95000 votes, hence the second runner up will get 85000
votes.

Now the remaining votes will be 500000-275000-95000-85000=45000

From
2, None of the candidates who contested in constituency C lost their
security deposit. The difference in votes polled by any pair of
candidates in this constituency was at least 10,000 => the person who
got 5th highest votes must have got > 600030/6 => $\ge$ 100006.
Since it is also given that the difference of votes is $\ge$ 10000,
the only possible case is winner, 1st runner up, 2nd runner up, 3rd
runner up, 4th runner up must have got
140006,130006,120006,110006,100006 respectively which sums upto exactly
600030.

Let the number of votes polled in D be 100x.

From 3, The winning candidate in constituency D must have got 5x+37500

The table now looks like:

In constituency B, the mark for not losing the security deposit is 1/6(325000) or 54,167.

But winner himself/herself got < 54167 => all the other candidates lost their security deposits.

11 is the correct answer,

7) Answer (D)

It’s given in the question that the first runner up polled 10,000
more votes than the second runner up in constituency A. Now the first
runner up has got 95000 votes, hence the second runner up will get 85000
votes.

Now the remaining votes will be 500000-275000-95000-85000=45000

From
2, None of the candidates who contested in constituency C lost their
security deposit. The difference in votes polled by any pair of
candidates in this constituency was at least 10,000 => the person who
got 5th highest votes must have got > 600030/6 => $\ge$ 100006.
Since it is also given that the difference of votes is $\ge$ 10000,
the only possible case is winner, 1st runner up, 2nd runner up, 3rd
runner up, 4th runner up must have got
140006,130006,120006,110006,100006 respectively which sums upto exactly
600030.

Let the number of votes polled in D be 100x.

From 3, The winning candidate in constituency D must have got  37500+5x.

The table now looks like:

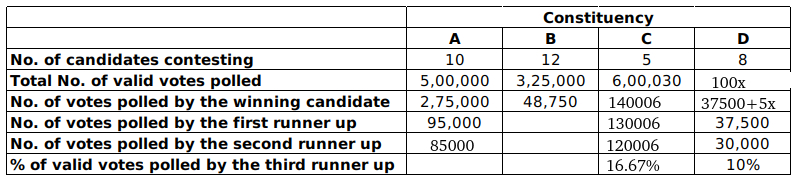
Number of votes polled to winning candidate must be 140006.

8) Answer (C)

It’s given in the question that the first runner up polled 10,000
more votes than the second runner up in constituency A. Now the first
runner up has got 95000 votes, hence the second runner up will get 85000
votes.

Now the remaining votes will be 500000-275000-95000-85000=45000

From
2, None of the candidates who contested in constituency C lost their
security deposit. The difference in votes polled by any pair of
candidates in this constituency was at least 10,000 => the person who
got 5th highest votes must have got > 600030/6 => $\ge$ 100006.
Since it is also given that the difference of votes is $\ge$ 10000,
the only possible case is winner, 1st runner up, 2nd runner up, 3rd
runner up, 4th runner up must have got
140006,130006,120006,110006,100006 respectively which sums upto exactly
600030.

From 3, Let the total votes in D be 100x => The winning candidate in constituency D must have got 37500+5x.

The table now looks like:

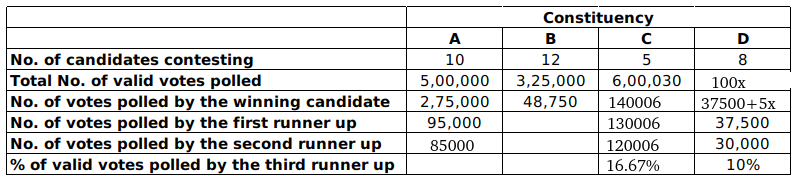
The candidates who didn’t lose the deposit must have got <16.67% => 3rd runner up must surely didn’t get the deposit.
Also,  the candidates who got security deposit must have got 65% of votes.
Case I:
Let top three candidates got the security deposit => 37500+5x+37500+30000 =65x => x=1750 => 100x= 175000

Case II:
Let top three candidates got the security deposit => 37500+5x+37500 =65x => 60x = 1250 => x=125000 but 16.66% of 125000 =20834  => 2nd runner up must got security deposit. So, this case is not valid.

The increasing order C will always come after D which is not happening in the third option. Hence that is the correct answer.

Download CAT Maths formulas PDF

9) Answer (C)

It’s given in the question that the first runner up polled 10,000
more votes than the second runner up in constituency A. Now the first
runner up has got 95000 votes, hence the second runner up will get 85000
votes.

Now the remaining votes will be 500000-275000-95000-85000=45000

From
2, None of the candidates who contested in constituency C lost their
security deposit. The difference in votes polled by any pair of
candidates in this constituency was at least 10,000 => the person who
got 5th highest votes must have got > 600030/6 => $\ge$ 100006.
Since it is also given that the difference of votes is $\ge$ 10000,
the only possible case is winner, 1st runner up, 2nd runner up, 3rd
runner up, 4th runner up must have got
140006,130006,120006,110006,100006 respectively which sums upto exactly
600030.

From 3, The winning candidate in constituency D must have got 1.05*37500 = 39375.

Let the number of votes polled in D be 100x.

The table now looks like:

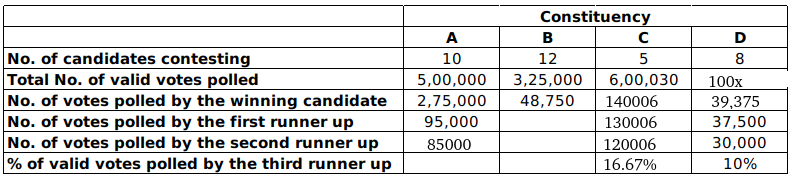
As calculated in the previous question, candidate D got 175000 votes. The winner got 5% more votes than first runner up, hence the winner got 0.05*175000 i.e 8750 more votes than first runner up . Thus 8750 is the winning margin for constituency D. Moreover margin in constituency is atleast 10000 . Hence in the increasing order C will always come after D which is not happening in the third option. Hence that is the correct answer.

Take Free CAT Daily Tests (With Video Solutions)

Join CAT 2021 Online Coaching

10) Answer (C)

It’s given in the question that the first runner up polled 10,000
more votes than the second runner up in constituency A. Now the first
runner up has got 95000 votes, hence the second runner up will get 85000
votes.

Now the remaining votes will be 500000-275000-95000-85000=45000

From
2, None of the candidates who contested in constituency C lost their
security deposit. The difference in votes polled by any pair of
candidates in this constituency was at least 10,000 => the person who
got 5th highest votes must have got > 600030/6 => $\ge$ 100006.
Since it is also given that the difference of votes is $\ge$ 10000,
the only possible case is winner, 1st runner up, 2nd runner up, 3rd
runner up, 4th runner up must have got
140006,130006,120006,110006,100006 respectively which sums upto exactly
600030.

From 3, Let the total votes in D be 100x => The winning candidate in constituency D must have got 37500+5x.

The table now looks like:

The candidates who didn’t lose the deposit must have got <16.67% => 3rd runner up must surely didn’t get the deposit.
Also, the candidates who got security deposit must have got 65% of votes.
Case I:
Let top three candidates got the security deposit => 37500+5x+37500+30000 =65x => x=1750 => 100x= 175000

Case II:
Let top three candidates got the security deposit => 37500+5x+37500
=65x => 60x = 1250 => x=125000 but 16.66% of 125000 =20834 =>
2nd runner up must got security deposit. So, this case is not valid.

For all the constituencies lets look at the candidates who lost their security deposit.

A (500000-275000-95000-85000)=45000.

B (325000-48750)=276250

C (0) and D (61250)=175000-46250-30000-37500

Hence percentage will be 382500/1600000× 100=23.91%

Download CAT Previous Solved Papers

Free Live Classes – Cracku Youtube

11) Answer: 2

There are only 2 configurations possible

12) Answer: 9

Maximum 9 red beads are possible as shown here

13) Answer: 6

To solve this question we can use the answer of the previous question, since maximum 9 red beads are possible, filling the remaining space with green and blue beads, in such a way that number of blue beads is minimised

Hence number of blue beads is 6

14) Answer: 6

6 more beads can be placed as shown

15) Answer (A)

Let’s look at all the students we have A,B,C,D,E,F,G,H. The guides are P,Q,R,S,T and they mentor 2,1,2,1,2 students respectively.

Slots are 9:00,9:30,10:00,10:30 . Moreover economics, sociology and anthropology have 4,3,1 students respectively.

Now from 5th statement, two sociology seminars and economics seminars are held in the same slot. This will not take place at 10:00(only one seminar is scheduled at 10:00), this will also not take place at 10:30( An anthropology seminar is scheduled at 10:30 and maximum three seminars are scheduled in a slot. Hence this will happen at either 9 or 9:30. Now from (7) A and G are scheduled in consecutive slots. A is scheduled at 10:00. Hence G will be scheduled at 9:30. SO from (5), there will be three students having their seminars at 9:30.

Combining this data with the remaining points we get the following table

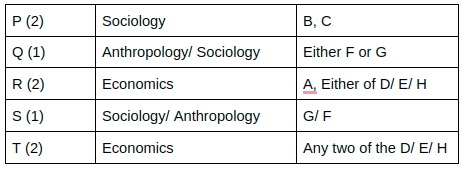
Moreover we do know that students having same subject are scheduled in consecutive slots. So we get

Here we can see that two seminars are scheduled in first slot.

16) Answer (D)

Let’s look at all the students we have A,B,C,D,E,F,G,H. The guides are P,Q,R,S,T and they mentor 2,1,2,1,2 students respectively.

Slots are 9:00,9:30,10:00,10:30 . Moreover economics, sociology and anthropology have 4,3,1 students respectively.

Now from 5th statement, two sociology seminars and economics seminars are held in the same slot. This will not take place at 10:00(only one seminar is scheduled at 10:00), this will also not take place at 10:30( An anthropology seminar is scheduled at 10:30 and maximum three seminars are scheduled in a slot. Hence this will happen at either 9 or 9:30. Now from (7) A and G are scheduled in consecutive slots. A is scheduled at 10:00. Hence G will be scheduled at 9:30. SO from (5), there will be three students having their seminars at 9:30.

Combining this data with the remaining points we get the following table

Moreover we do know that students having same subject are scheduled in consecutive slots. So we get

As we can see from the above table, P,Q and S are not guiding any economics student

Take Free CAT Video Lectures

17) Answer (B)

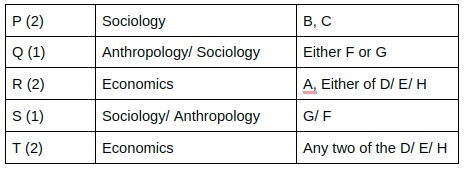
As we can clearly say from here that H/D/E are all economics students. Hence Option B is definitely correct

18) Answer (D)

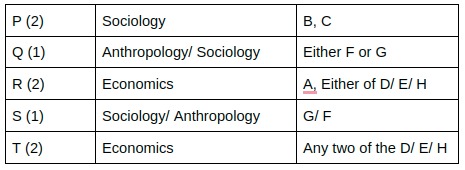
Now D is scheduled in a slot later than Q. Q can mentor only F or G, but obviously he can’t mentor F because F is in the last slot, hence Q will mentor G. In that scenario D has to take the 10:30 slot which means D will  be mentored by R and E/H will be mentored by T. So statement 1 and statement 2 both are correct.

19) Answer (C)

If E and Q are scheduled in the same slot, they both can be in the last slot. In that case E will be guided by R and both D and H will be guided by T.  Moreover if they are in the second slot, E will be guided by T and atleast one of D and H will be guided by T. Hence option (c) is correct

20) Answer (B)

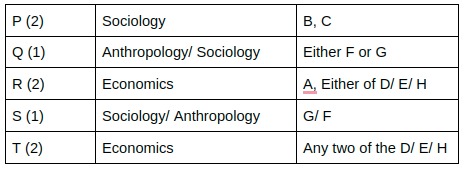
Now D is scheduled in the slot immediately before Q. In that case Q will be in the 9:30 slot and D will be in the 9:00 am slot. Hence D will be mentored by T and one of E/H will be mentored  by R and the other by T. Obviously E is guided by R is not necessarily true as he can be mentored by T also.

Free Live Classes – Cracku Youtube

21) Answer (D)

following is the order of arrival and departure of cars

As we can see that car 2 and car 7 are parked next to car 3

22) Answer (D)

Let’s look at option 4.

Order of cars is 8,2,3,V,5,6,7. This sequence is easily possible.

Let’s say cars 1,2,3,4,5,6,7 arrive one after the another.

Now Car 1 leaves and Car 8 takes that place.

Finally Car 4 leaves. Hence we can see that this combination of cars is possible

23) Answer (C)

The original sequence as given in the question is 4,5,6,V,3

This is possible when cars 1,2,3 arrived and then cars 1 and 2 leave. After that cars 4,5 and 6 arrive.

Now there are 4 slots to the left of car 3. This is only possible when cars 1 and 2 were SUVs. Now out of these 4 slots,

3 slots are occupied by cars 4,5 and 6. As a result these are compact cars . Car 3 can be a SUV or a Compact car and it won’t impact the final solution.

24) Answer (D)

Here we can see that cars 3 and 5 are still in their position. Thus car 4 was not the first car to leave, either 1 or 2 left before 4. Let’s say only car 2 left before car 4. Now supposingly if car 2 is an SUV, car 6 was parked in that lot. Thus car 2 and car 7 are compact cars. Option 4 is correct.

Free CAT online Material

Free CAT preparation App

We hope this  for CAT 2020 LRDI Question Paper With Answers PDF with Solutions will be helpful to you.