Boat And Stream Questions For SBI Clerk
Download SBI Clerk Boat And Stream Questions & Answers PDF for SBI Clerk Prelims and Mains exam. Very Important SBI Clerk Boat And Stream questions on with solutions.
Download Boat And Stream Questions For SBI Clerk
490 Banking mocks for Rs. 299 – Enroll here
Take a free mock test for SBI Clerk
Download SBI Clerk previous papers PDF
Question 1: A boat takes 12 hours to reach point B from point A. It takes 6 hours to reach point A from point B. The river flows from A to B. How much time will it take to travel from A to B if the river remains still?
a) 9 hours
b) 10 hours
c) 8 hours
d) 7.5 hours
e) 10.5 hours
Question 2: A boat develops a leak 18 km from the shore. The ship is still able to move at 12 km/hr and can move only for 25 minutes. A rescue boat which takes 5 minutes to evacuate the crew of the boat leaves the shore at the same time. What should be the minimum speed of the rescue boat to successfully evacuate the crew from the boat in time?
a) 36 kmph
b) 44 kmph
c) 38 kmph
d) 42 kmph
e) 40 kmph
Question 3: There is a river which flows from west to east at a speed of 5 m/s. Arjun, is standing at one bank of the river. He decides to use his motorboat to reach the other bank of the river. His boat travels at a constant speed of 10 m/s. He wants to travel in such a manner that he reaches a point on the other side which is perpendicularly opposite to his starting point. Find the time he takes to reach other side of the bank if the width of the river is 60 meters.
a) $5\sqrt{2}$ seconds
b) $6$ seconds
c) $12$ seconds
d) $4\sqrt{3}$ seconds
e) $6\sqrt{2}$ seconds
Question 4: A boat takes 2 hours to travel from point A to B in still water .To find out it’s speed up-stream ,which of the following information is needed.
i. Distance between point A and B
Ii.Time taken to travel down stream from B to A
iii. Speed of the stream of the water
iv. Effective speed of Boat while traveling Downstream from B to A
a) All are required
b) Even these we cannot found the answer
c) Only i,iii, and either ii or iv
d) Only i and iii
e) None of these
Download SBI Clerk Previous Papers PDF
Take a free mock test for SBI Clerk
Question 5: The speed of the boat in still water is 24 kmph and the speed of the stream is 41cm/h. The time taken by the boat to travel from A to B downstream is 36 minutes less than the time taken by the same boat to travel from B to’C upstream. If the distance between A and B is 4 km more than the distance between B and C, what is the distance between A and B?
a) 112 km
b) 1401cm
c) 56 km
d) 841cm
e) 281cm
Question 6: A man takes 2.2 times as long to row a distance upstream as to row the same distance downstream. If he can row 55 km downstream in 2 hours 30 minutes, what is the speed of the boat in still water? (in km/h)
a) 40
b) 8
c) 16
d) 24
e) 32
Question 7: A boat takes a total time of twelve hours to travel 105 kms upstream and the same distance downstream. The speed of the boat in still water is six times of the speed of the current. What is the speed of the boat in still water? (in km/hr)
a) 12
b) 30
c) 18
d) 24
e) 36
Question 8: A boat takes a total time of eight hours to travel 63 kms upstream and the same distance downstream. The speed of the current is ${1 \over 8}$th of the speed of the boat in still water. What is the speed of the boat in still water? (in km/hr)
a) 32
b) 24
c) 16
d) 8
e) 38
Question 9: A boat takes six hours to travel a certain distance downstream and five hours to travel a certain distance upstream. The distance travelled upstream is half of the travelled downstream. If the speed of the current is 4 km/hr, what is the speed of the boat in still water? (in km/hr)
a) 16
b) 20
c) 24
d) 10
e) 18
Banking Study Material – 18000 Questions
Question 10: A boatman can row a boat downstream at 13 kmph and upstream at 9 kmph. What will be the speed of boat in still water ? (in kmph).
a) 12
b) 10.5
c) 11
d) 10
e) 11.5
Question 11: A boat goes downstream at the rate of 9 kmph and upstream at the rate of 6 kmph. Find the speed of current.
a) 1.5 kmph
b) 2 kmph
c) 7.5 kmph
d) 4.5 kmph
e) None of these
Question 12: A boatman rows downstream a distance of 30 km in 6 hours and up stream a distance of 24 km in 6 hours. The ratio of speed of boat in still water and speed of current is
a) 9 : 1
b) 8 : 1
c) 9 : 2
d) 8 : 3
e) None of these
Question 13: A boat starts from A and travels towards B which is 72 km from A. As soon as the boat reaches B, it turns back and heads towards A. If the speed of the boat is 600 percent more than the speed of the stream and total travel time is 7 hours then find the time required the same boat to travel 36 km upstream?
a) 2 hours
b) 4 hours
c) 3.5 hours
d) 2.5 hours
e) 1.5 hours
Question 14: There is a road along the river. The speed of the river is 2 m/s and the speed of the boat is 10 m/s. Two friends decided to have a race in which Arun will cycle till P, which is 96m from the starting point, and return back to the starting point. Sam will use the boat to reach P and return. The speed of the cycle is 10 m/s. Which of the following is true?
a) Arun takes 6% less time than Sam to finish the race
b) Both of them reach the starting point at the same time.
c) Arun takes 4% less time than Sam to finish the race
d) Arun takes 4% more time than Sam to finish the race
e) Arun takes 6% less time than Sam to finish the race.
Question 15: The sum of the speed of the boat A downstream and the speed of the boat B upstream is 27km/h. If the speed of boat A in still water is 3km/h less than that of boat B, what is the respective ratio between the speed of boat A in still water and that of boat B in still water? (Considering the speed of current to be constant)
a) 4 : 5
b) 2 : 5
c) 2 : 3
d) 3 : 5
e) 3 : 4
Question 16: A boat travels from A to B upstream and then from B to C downstream taking the same time. The respective ratio between the distance from A to B and the distance from B to C is 5 : 7. If the boat takes 2 hours 30 min to travel a distance of 35 km downstream, what is the speed of the stream ? (in km/h)
a) 2 km/h
b) 1.5 km/h
c) 2.5 km/h
d) 2.2 km/h
e) None of these
Question 17: The time taken by a boat to travel ‘x’ km upstream is twice the time taken by the same boat to travel ‘x’ km downstream. If speed of the boat in still water is 12 km/h, what is the speed of current ? (in km/h)
a) 3
b) 4
c) 3.5
d) 4.5
e) None of these
Question 18: The speed of a boat in still water is 500% more than the speed of the current. What is the respective ratio between the speed of the boat downstream and speed of the boat upstream ?
a) 9 : 2
b) 7 : 3
c) 7 : 5
d) 9 : 4
e) 4 : 3
Question 19: The distance between two points is 36 km. A boat rows in still water at 6 kmph. It takes 8 hours less to cover this distance in downstream in comparison to that in upstream. The rate of stream is
a) 3 kmph
b) 2 kmph
c) 2.5 kmph
d) 4 kmph
e) None of these
Question 20: The speed of a boat B downstream is 40 km/hr and the speed of the same boat in still water is 30km/hr. If the speed of the stream suddenly rises by 20%, what is the time taken by the boat to cover 450m in upstream direction?
a) 1 min
b) 1.8 mins
c) 1.2 mins
d) 1.9 mins
e) 1.5 mins
General Knowledge Questions & Answers PDF
Answers & Solutions:
1) Answer (C)
Let the speed of the boat be ‘b’ and the speed of the stream be ‘s’.
Let the distance between A and B be ‘D’.
We know that D/(b-s) = 12.
D = 12b – 12s ——–(1).
We also know that D/(b+s) = 6.
D = 6b + 6s ———-(2)
Equating (1) and (2), we get,
12b – 12s = 6b + 6s
=> 6b = 18s
b = 3s.
D = 12*3s – 12*s
D = 24s.
Time taken to travel from A to B in still water = D/b = 24s/3s = 8 hours.
Therefore, option C is the right answer.
2) Answer (D)
Distance between Boat and shore = 18 km
The rescue boat must reach the leaking boat in 20 minutes as 5 minutes is needed for evacuation.
Let the relative velocity of the 2 boats be ‘v’
So, v = $\frac{18}{20}$ km per min = 18*60/20 kmph = 54 kmph
So minimum speed of the rescue boat = 54 – 12 = 42 kmph
Hence, option D is correct option.
3) Answer (D)
Since he wants to reach a point which is perpendicularly opposite, he should ensure that the horizontal displacement is zero.
Hence, his horizontal component of the speed should be 5 m/s east to west.
Let’s represent it in a diagram,
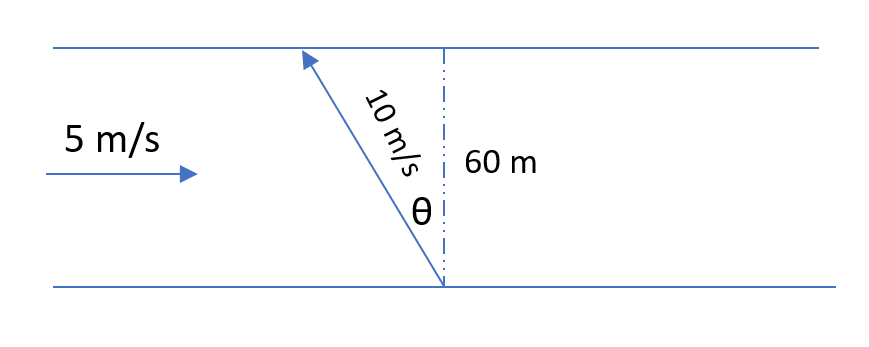
His speed in the horizontal direction = $10 \sin \theta$
His speed in the vertical direction = $10 \cos \theta$
$10 \sin \theta = 5$
Hence, $\theta$ = 30°
His speed in vertical direction = $10 \cos 30$ = $5 \sqrt{3}$
Time taken to cover a vertical distance of 60m = $\frac{60}{5\sqrt{3}}$ = $4\sqrt{3}$ seconds.
4) Answer (D)
Time taken by boat to travel from point A to B in still water = 2 hours
To find the upstream speed, we definitely need the speed of stream, thus statement (iii) is mandatory.
Also, the distance between points A and B or the speed of boat in still water is needed.
Thus, statements (i) and (iii) are required to find the upstream speed of the boat.
=> Ans – (D)
5) Answer (C)
6) Answer (C)
Let speed of boat in still water = $x$ km/hr
=> Speed of current = $y$ km/hr
Let distance travelled = $d$ km
Acc. to ques, => $2.2 (\frac{d}{x + y}) = \frac{d}{x – y}$
=> $2.2x – 2.2y = x + y$
=> $2.2x – x = y + 2.2y$
=> $3x = 8y$ ————-(i)
Also, the man takes 2 hrs 30 mins in travelling 55 km downstream.
=> $\frac{55}{x + y} = 2 + \frac{1}{2}$
=> $\frac{55}{x + y} = \frac{5}{2}$
=> $x + y = 22$
Multiplying both sides by 8, and using eqn(i), we get :
=> $8x + 3x = 22 \times 8$
=> $x = \frac{22 \times 8}{11} = 16$ km/hr
7) Answer (C)
Let speed of current = $x$ km/hr
=> Speed of boat in still water = $6x$ km/hr
Acc. to ques, => $\frac{105}{7x} + \frac{105}{5x} = 12$
=> $\frac{15}{x} + \frac{21}{x} = 12$
=> $\frac{36}{x} = 12$
=> $x = \frac{36}{12} = 3$
$\therefore$ Speed of boat in still water = $6 \times 3 = 18$ km/hr
8) Answer (C)
Let speed of current = $x$ km/hr
=> Speed of boat in still water = $8x$ km/hr
Acc. to ques, => $\frac{63}{9x} + \frac{63}{7x} = 8$
=> $\frac{7}{x} + \frac{9}{x} = 8$
=> $\frac{16}{x} = 8$
=> $x = \frac{16}{8} = 2$
$\therefore$ Speed of boat in still water = $8 \times 2 = 16$ km/hr
9) Answer (A)
Let speed of boat in still water = $x$ km/hr
Let distance travelled downstream = $2d$ km
=> Distance travelled upstream = $d$ km
Using, $time = \frac{distance}{speed}$
=> $6 = \frac{2d}{x + 4}$ ———(i)
and $5 = \frac{d}{x – 4}$ ———(ii)
Dividing eqn(i) from (ii), we get :
=> $\frac{6}{5} = \frac{\frac{2d}{x + 4}}{\frac{d}{x – 4}}$
=> $\frac{6}{5} = \frac{2 (x – 4)}{x + 4}$
=> $6x + 24 = 10x – 40$
=> $10x – 6x = 24 + 40 = 64$
=> $x = \frac{64}{4} = 16$ km/hr
10) Answer (C)
Speed of boat in still water
= $\frac{1}{2}$ (downstream + upstream)
= $\frac{1}{2} (13 + 9) = \frac{22}{2}$
= $11$ kmph
11) Answer (A)
Speed of current = $\frac{1}{2}$ (downstream – upstream)
= $\frac{1}{2} (9 – 6)$
= $\frac{3}{2} = 1.5$ kmph
12) Answer (A)
Let speed of boat in still water = $x$ km/h
and speed of current = $y$ km/h
Now, $\frac{30}{x + y} = 6$
=> $x + y = 5$
and $\frac{24}{x – y} = 6$
=> $x – y = 4$
Solving above equations, we get :
$x = \frac{9}{2}$ and $y = \frac{1}{2}$
=> $x : y = 9 : 1$
13) Answer (A)
Let speed of the stream be ‘x’, then the speed of the boat will be 7x
We have been given that
72/8x + 72/6x = 7
=> x = 3
Hence, the speed of the boat is 21 km/hr
Hence, required time = 36/2 = 2 hours
Thus, the correct answer is option A
14) Answer (C)
Arun cycles at a constant speed of 10 m/s.
Hence, he takes 192/10 = 19.2 seconds to complete the race.
Sam has to cover upstream in one direction and downstream in the other direction.
Time taken by him to cover upstream distance = 96/(10 -2) = 12 seconds.
Time taken by him to cover downstream distance = 96/(10 + 2) = 8 secons
Hence, he takes 20 seconds to complete the race.
The difference in their times = 0.8 seconds
Percentage = 0.8/20 *100 = 4%
15) Answer (A)
Let speed of boat A in still water = $x$ kmph
=> Speed of boat B in still water = $(x + 3)$ kmph
Let speed of current = $y$ kmph
Acc to ques,
=> $(x + y) + (x + 3 – y) = 27$
=> $2x = 27 – 3 = 24$
=> $x = \frac{24}{2} = 12$ kmph
Speed of B = 12 + 3 = 15 kmph
$\therefore$ Required ratio = 12 : 15
= 4 : 5
16) Answer (A)
Let distance between AB = $5x$ and BC = $7x$
Downstream speed = $\frac{35}{2.5} = 14$ km/h
Let upstream speed = $y$ km/h
Now, $time = \frac{distance}{speed}$
=> $\frac{5x}{y} = \frac{7x}{14}$
=> $\frac{5}{y} = \frac{1}{2}$
=> $y = 5 \times 2 = 10$ km/h
Now, speed of stream = $\frac{1}{2}$ (downstream – upstream)
= $\frac{1}{2} (14 – 10)$
= $\frac{4}{2} = 2$ km/h
17) Answer (B)
REASONING
18) Answer (C)
Let speed of current = $x$ km/h
=> Speed of boat in still water = $x + (\frac{500}{100} \times x)$
= $x + 5x = 6x$ km/h
=> Speed of the boat downstream = $6x + x = 7x$ km/h
Speed of boat upstream = $6x – x = 5x$ km/h
$\therefore$ Required ratio = $\frac{7x}{5x}$
= $7 : 5$
19) Answer (A)
Let speed of stream = $x$ kmph
=> Speed of boat downstream = $(6 + x)$ kmph
Speed upstream = $(6 – x)$ kmph
Using, $time = \frac{distance}{speed}$
=> $\frac{36}{6 – x} – \frac{36}{6 + x} = 8$
=> $\frac{1}{6 – x} – \frac{1}{6 + x} = \frac{8}{36}$
=> $\frac{(6 + x) – (6 – x)}{(6 + x) (6 – x)} = \frac{2}{9}$
=> $\frac{2x}{36 – x^2} = \frac{2}{9}$
=> $\frac{x}{36 – x^2} = \frac{1}{9}$
=> $36 – x^2 = 9x$
=> $x^2 + 9x – 36 = 0$
=> $x^2 + 12x – 3x – 36 = 0$
=> $x (x + 12) – 3 (x + 12) = 0$
=> $x = 3 , -12$
$\because$ Speed cant be negative, => $x = 3$ kmph
20) Answer (E)
Downstream speed of boat B is = speed of boat B in still water + speed of stream.
So Speed of stream = 40-30 = 10 km/hr.
If speed of stream increase by 20%, new speed = 10 * 1.2 = 12km/hr
So Time required to cover upstream distance of 450m = 0.45 / (30-12) = 0.025 hr = 1.5 mins
So E is the right choice.
We hope this Boat And Stream Question & Answers PDF of SBI Clerk is very Useful for preparation of SBI Clerk Exams.





