Angles Questions for NMAT – Download [PDF]

Download Angles Questions for NMAT PDF – NMAT Fill in the blanks questions pdf by Cracku. Top 10 very important Angles Questions for NMAT based on asked questions in previous exam papers.

Download Angles Questions for NMAT

Get 5 NMAT Mocks for Rs. 499

Take NMAT mock test

Question 1: Which of the following can’t be the ratio of angles of an acute angled triangle?

a) 1:9:9

b) 2:3:4

c) 3:7:8

d) 1:1:1

e) 1:2:3

Question 2: Two right angled triangles ABC and DCB are drawn on the same side of BC. If BC = 30, AB = 10 and CD = 15, and AC and BD intersect at P, find the distance of P from BC.

a) 8 cm

b) 6 cm

c) 10 cm

d) 5 cm

e) 7 cm

Question 3: Two sides of a plot measure 32 m and 24 m and the angle between them is a perfect right angle. The other two sides measure 25 m each and the other three angles are not right angles. What is the area of the plot?
[CAT 2001]

a) 768 $m^2$

b) 534 $m^2$

c) 696.5 $m^2$

d) 684 $m^2$

Question 4: Consider obtuse-angled triangles with sides 8 cm, 15 cm and x cm. If x is an integer then how many such triangles exist?

[CAT 2008]

a) 5

b) 21

c) 10

d) 15

e) 14

Question 5: Consider obtuse-angled triangles with sides 8 cm, 15 cm and x cm. If x is an integer then how many such triangles exist?

a) 5

b) 21

c) 10

d) 15

e) 14

Question 6: 2 polygons with (n-1) and (n+2) sides respectively have their exterior angles in such a way that the difference between the exterior angles is 6 degrees. What is the value of n?

a) 11

b) 15

c) 12

d) 13

Question 7: What is the number of distinct triangles with integral valued sides and perimeter 14?[CAT 2000]

a) 6

b) 5

c) 4

d) 3

Question 8: The sum of all interior angles of an isosagon ?

a) 3240$^{\circ}$

b) 360$^{\circ}$

c) 720$^{\circ}$

d) 900$^{\circ}$

Question 9: If two complementary angles are in the ratio 1: 4, find the supplement of larger angle ?

a) 157.5$^{\circ}$

b) 108$^{\circ}$

c) 137.5$^{\circ}$

d) 120$^{\circ}$

Question 10: A pair of parallel lines are cut by a transversal and the sum of a pair of alternate interior angles A and B is 100 degrees. What is the sum of the pair of corresponding angles that has A as one of its angles?

a) 180 degrees

b) 100 degrees

c) 260 degrees

d) None of the above

Join 7K MBA Aspirants Telegram Group

Download Highly Rated CAT preparation App

Answers & Solutions:

1) Answer (E)

In an acute angled triangle, the sum of the smallest two angles is greater than the third angle. If the ratio is 1:2:3, the angles are 30, 60 and 90 which is a right angled triangle.

2) Answer (B)

Let PT be the perpendicular drawn from P to BC.
Let PT be ‘y’. Let CT be ‘x’. This means BT = 30-x

Triangles ABC and PTC are similar.
=> $\frac{PT}{AB}=\frac{CT}{BC} => \frac{y}{10}=\frac{x}{30}$ —– (1)

Triangles DBC and PBT are similar.
=> $\frac{PT}{CD}=\frac{BT}{BC} => \frac{y}{15}=\frac{30-x}{30}$ —– (2)

Solving equations (1) and (2) we get y = 6 => PT = 6 cm.

3) Answer (D)

Length of the diagonal of the right triangle is 40. The height of the isosceles triangle formed, with 40 as its base is 15.
So, area = $\frac{1}{2}* 32 * 24 + \frac{1}{2} * 40 * 15 = 384 + 300 = 684 m^2$

4) Answer (C)

For obtuse-angles triangle, $c^2 > a^2 + b^2$ and c < a+b

If 15 is the greatest side, 8+x > 15 => x > 7 and 225 > 64 + x^2 => x^2 < 161 => x <= 12

So, x = 8, 9, 10, 11, 12

If x is the greatest side, then 8 + 15 > x => x < 23

x^2 > 225 + 64 = 289 => x > 17

So, x = 18, 19, 20, 21, 22

So, the number of possibilities is 10

5) Answer (C)

For obtuse-angles triangle, $c^2 > a^2 + b^2$ and c < a+b
If 15 is the greatest side, 8+x > 15 => x > 7 and $225 > 64 + x^2 => x^2 < 161 => x <= 12$
So, x = 8, 9, 10, 11, 12
If x is the greatest side, then 8 + 15 > x => x < 23
$x^2$ > 225 + 64 = 289 => x > 17
So, x = 18, 19, 20, 21, 22
So, the number of possibilities is 10

6) Answer (D)

The exterior angles are given by 360/(n-1) and 360/(n+2)
So, 360/(n-1) – 360/(n+2) = 6 => 720 + 360 = 6(n^2 -3n – 2) => (n-1)(n+2) = 180.
15*12 = 180, so, n-1 =12 and n+2 = 15 and n = 13

7) Answer (C)

Let the sides be x, y and 14-(x+y)
x+y > 14-(x+y) => x+y > 7
x+14-x-y > y => y < 7
Similarly, x < 7
If x = 1, y = 7 (not possible)
So, if x = 2, y = 6
if x = 3, y = 5
if x = 4, y = 4, 5
The cases for x = 5 and 6 are already taken care of by y.
Number of possible cases = 4

8) Answer (A)

Isosagon is a regular polygon with 20 sides.

Sum of interior angles = (n-2)*180; where n is the number of sides.

Sum of angles = (20-2)*180 = 3240

9) Answer (B)

Let the two angles be X and 90-X.
Hence, X = 4(90-X) or X = 72 $^{\circ}$
Hence, the supplement of the larger angle is
180$^{\circ}$ – 4/5(90$^{\circ}$)=108$^{\circ}$

10) Answer (B)

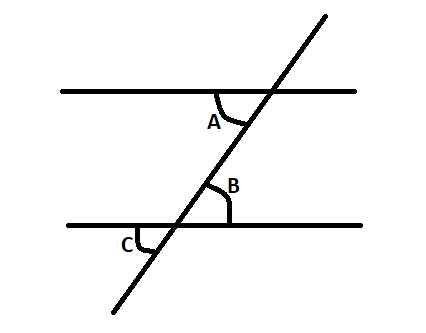
Since A and B are alternate interior angles, they are equal and each is equal to 50 degrees. Since corresponding angles are equal, the sum of A and its corresponding angle, say C is 50+50 = 100 degrees.

We hope these Angles Questions for NMAT pdf for the NMAT exam will be highly useful for your Preparation.