Lines and Angles Questions for SSC CGL PDF
Download SSC CGL Lines and Angles Questions with answers PDF based on previous papers very useful for SSC CGL exams. Very Important Lines and Angles Questions for SSC exams
Download Lines and Angles Questions for SSC CGL
Get 200 SSC mocks for just Rs. 249. Enroll here
Take a free mock test for SSC CGL
Download SSC CGL Previous Papers PDF
More SSC CGL Important Questions and Answers PDF
Question 1: BC is the centre of the circle with centre O. A is a point on major arc BC as shown in the above figure. What is the value of $\angle{BAC}+\angle{OBC}$ ?

a) 120$^{\circ}$
b) 60$^{\circ}$
c) 90$^{\circ}$
d) 180$^{\circ}$
Question 2: AC and BC are two equal cords of a circle. BA is produced to any point P and CP, when joined cuts the circle at T. Then
a) CT : TP = AB : CA
b) CT : TP = CA : AB
c) CT : CB = CA : CP
d) CT : CB = CP : CA
Question 3: If an obtuse-angled triangle ABC, is the obtuse angle and O is the orthocenter. If = 54$^{\circ}$ , then is
a) 108$^{\circ}$
b) 126$^{\circ}$
c) 136$^{\circ}$
d) 116$^{\circ}$
Question 4: The external bisectors of and of meet at point P. If = 80$^{\circ}$ , the is
a) 50$^{\circ}$
b) 40$^{\circ}$
c) 80$^{\circ}$
d) 100$^{\circ}$
Question 5: In a triangle ABC, $\angle{A} = 90^o , \angle{C} = 55^o , \overline{AD}$ is perpendicular to $\overline{BC}$. What is the value of $\angle{BAD}$ ?
a) 60 $^{\circ}$
b) 45 $^{\circ}$
c) 55 $^{\circ}$
d) 35 $^{\circ}$
Question 6: If O be the circumcentre of a triangle PQR and $\angle{QOR} = 110^o, \angle{OPR} = 25^o$, then the measure of $\angle{PRQ}$ is
a) 50 $^{\circ}$
b) 55 $^{\circ}$
c) 60 $^{\circ}$
d) 65 $^{\circ}$
SSC CGL Previous Papers Download PDF
Question 7: A, B, C, D are four points on a circle. AC and BD intersect at a point such that $\angle{BEC} = 130^o$ and $\angle{ECD} = 20^o$. Then, $\angle{BAC}$ is
a) 90 $^{\circ}$
b) 100 $^{\circ}$
c) 110 $^{\circ}$
d) 120 $^{\circ}$
Question 8: ABC is a triangle. The bisectors of the internal angle $\angle$B and external $\angle$C intersect at D. If $\angle$BDC=$50^{\circ}$, then $\angle$A is
a) $100^{\circ}$
b) $90^{\circ}$
c) $120^{\circ}$
d) $60^{\circ}$
Question 9: In a triangle ABC, the side BC is extended up to D. Such that CD = AC, if angleBAD = $109°$ and angleACB=$72°$ then the value of angleABC is
a) $35°$
b) $60°$
c) $40°$
d) $45°$
Question 10: The line passing through (-2,5) and (6,b) is perpendicular to the line 20x + 5y = 3. Find b?
a) -7
b) 4
c) 7
d) -4
Question 11: The co-ordinates of the centroid of a triangle ABC are (-1,-2) what are the co-ordinates of vertex C, if co-ordinates of A and B are (6,-4) and (-2,2) respectively?
a) (-7,-4)
b) (7,4)
c) (7,-4)
d) (-7,4)
Question 12: Find equation of the perpendicular bisector of segment joining the points (2,-6) and (4,0)?
a) x + 3y = 6
b) x + 3y = -6
c) x – 3y = -6
d) x – 3y = 6
Question 13: In what ratio is the segment joining (12,1) and (3,4) divided by the Y axis?
a) 4:1
b) 1:4
c) 4:3
d) 3:4
Question 14: The line passing through (4,3) and (y,0) is parallel to the line passing through (1,2) and (3,0). Find y?
a) 1
b) 7
c) 2
d) 5
Question 15: What is the slope of the line perpendicular to the line passing through the points (8,2) and (3,1)?
a) -5
b) 3/5
c) 5/3
d) 1/5
18000+ Questions – Free SSC Study Material
Answers & Solutions:
1) Answer (C)
As we know that angle through an arc on centre is double that of made on remaining arc.
Hence $\angle{BOC}=2\angle{BAC} $=2x (where x=$\angle{BAC} $)
and $\angle{OBC}$ would be 90-x
So $\angle{BAC}+\angle{OBC}$=90
2) Answer (C)
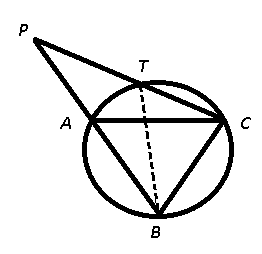
It is given that AC = BC, also $\triangle$ PTB and $\triangle$ PAC are similar, we have :
$\frac{CA}{CP}=\frac{BT}{BP}$ —————-(i)
Also, we have $\angle$ PBC = $\angle$ BTC ($\because$ $\angle$ PBC = $\angle$ BAC = $\angle$ BTC) and $\angle$ PCB = $\angle$ BCT
=> $\triangle$ PBC $\sim$ $\triangle$ BTC
Thus, $\frac{CB}{BP}=\frac{CT}{BT}$
=> $\frac{BT}{BP}=\frac{CT}{CB}$ ————–(ii)
From equations (i) and (ii), we get :
$\frac{CA}{CP}=\frac{CT}{CB}$
=> Ans – (C)
3) Answer (B)
4) Answer (A)
5) Answer (C)
$\angle A = 90^o$
$\angle C = 55^o$
$\angle B$ will be $180 – (90+55) = 35^o$
As AD is perpendicular to BC Hence $\angle BAD=180-(90+35)=55^o$
6) Answer (C)
As we know circumcentre O is perpendicular bisector of sides of a triangle.
And $\angle QOR = 110^o$
and OQ=OR (radius) hence angles OQR and ORQ will be also be equal.
Which will have value equal to $\frac{180-110}{2} = 35^o$
Now angle OPR and PRO will also have equal value as $25^o$.
So angle PQR will be 35+25 = $60^o$
7) Answer (C)
Angle ABD will be equal to angle ACD = $20^o$ (same sector angles)
Angle BEC = $130^o$ so angle AED = $130^o$ (concurrent angles)
Now angle BEA will be $\frac{360-130-130}{2} = 50^o$
So angle EDC will be $180-(50+20) = 110^o$
8) Answer (A)
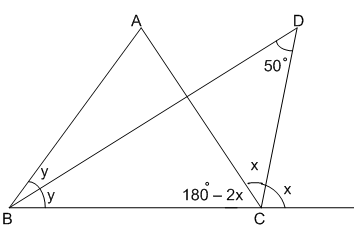
In $\triangle$ BDC,
=> $y+(180^\circ-2x+x)+50^\circ=180^\circ$
=> $y-x+50^\circ=0$
=> $y-x=-50^\circ$
In $\triangle$ ABC,
=> $2y+(180^\circ-2x)+\angle A=180^\circ$
=> $2(y-x)+\angle A=0$
=> $2(-50^\circ)+\angle A=0$
=> $\angle A=100^\circ$
=> Ans – (A)
9) Answer (A)

Angle ACB =72$^o$
Angle ACD = 108$^o$
Angle CAD = Angle ADC = 36$^o$
Angle BAD = Angle BAC + Angle CAD =109$^o$
Angle BAC = 73$^o$
Angle ABC = 180 – Angle BAC – Angle ACB = 180 – 73 – 72 = 35$^o$
Hence Option A is the correct answer.
10) Answer (C)
Slope of line having equation : $ax + by + c = 0$ is $\frac{-a}{b}$
=> Slope of line $20x + 5y = 3$ is $\frac{-20}{5} = -4$
Slope line passing through (-2,5) and (6,b) = $\frac{b – 5}{6 + 2} = \frac{(b – 5)}{8}$
Also, product of slopes of two perpendicular lines is -1
=> $\frac{(b – 5)}{8} \times -4 = -1$
=> $b – 5 = \frac{8}{4} = 2$
=> $b = 2 + 5 = 7$
=> Ans – (C)
11) Answer (A)
Coordinates of centroid of triangle with vertices $(x_1 , y_1)$ , $(x_2 , y_2)$ and $(x_3 , y_3)$ is $(\frac{x_1 + x_2 + x_3}{3} , \frac{y_1 + y_2 + y_3}{3})$
Let coordinates of vertex C = $(x , y)$
Vertex A(6,-4) and Vertex B(-2,2) and Centroid = (-1,-2)
=> $-1 = \frac{-2 + 6 + x}{3}$
=> $x + 4 = -1 \times 3 = -3$
=> $x = -3 – 4 = -7$
Similarly, => $-2 = \frac{-4 + 2 + y}{3}$
=> $y – 2 = -2 \times 3 = -6$
=> $y = -6 + 2 = -4$
$\therefore$ Coordinates of vertex C = (-7,-4)
=> Ans – (A)
12) Answer (B)
Let line $l$ perpendicularly bisects line joining A(2,-6) and B(4,0) at C, thus C is the mid point of AB.
=> Coordinates of C = $(\frac{2 + 4}{2} , \frac{-6 + 0}{2})$
= $(\frac{6}{2} , \frac{-6}{2}) = (3,-3)$
Now, slope of AB = $\frac{y_2 – y_1}{x_2 – x_1} = \frac{(0 + 6)}{(4 – 2)}$
= $\frac{6}{2} = 3$
Let slope of line $l = m$
Product of slopes of two perpendicular lines = -1
=> $m \times 3 = -1$
=> $m = \frac{-1}{3}$
Equation of a line passing through point $(x_1,y_1)$ and having slope $m$ is $(y – y_1) = m(x – x_1)$
$\therefore$ Equation of line $l$
=> $(y + 3) = \frac{-1}{3}(x – 3)$
=> $3y + 9 = -x + 3$
=> $x + 3y = 3 – 9 = -6$
=> Ans – (B)
13) Answer (A)
Using section formula, the coordinates of point that divides line joining A = $(x_1 , y_1)$ and B = $(x_2 , y_2)$ in the ratio a : b
= $(\frac{a x_2 + b x_1}{a + b} , \frac{a y_2 + b y_1}{a + b})$
Let the ratio in which the segment joining (12,1) and (3,4) divided by the y-axis = $k$ : $1$
Since, the line segment is divided by y-axis, thus x coordinate of the point will be zero, let the point of intersection = $(0,y)$
Now, point P (0,y) divides (12,1) and (3,4) in ratio = k : 1
=> $0 = \frac{(3 \times k) + (12 \times 1)}{k + 1}$
=> $3k + 12 = 0$
=> $k = \frac{-12}{3} = -4$
$\therefore$ Line segment joining (12,1) and (3,4) is divided by the Y axis in the ratio = 4 : 1 externally
=> Ans – (A)
14) Answer (B)
Slope of line passing through $(x_1,y_1)$ and $(x_2,y_2)$ is $\frac{y_2 – y_1}{x_2 – x_1}$
=> Slope of line passing through (1,2) and (3,0) = $\frac{0 – 2}{3 – 1} = \frac{-2}{2} = -1$
Slope of line passing through (4,3) and (y,0) = $\frac{0 – 3}{y – 4} = \frac{-3}{(y – 4)}$
Also, slopes of parallel lines are equal.
=> $\frac{-3}{y – 4} = -1$
=> $y – 4 = 3$
=> $y = 3 + 4 = 7$
=> Ans – (B)
15) Answer (A)
Slope of line passing through $(x_1,y_1)$ and $(x_2,y_2)$ is $\frac{y_2 – y_1}{x_2 – x_1}$
=> Slope of line passing through (3,1) and (8,2) = $\frac{2 – 1}{8 – 3} = \frac{1}{5}$
Let slope of line perpendicular to it = $m$
Also, product of slopes of two perpendicular lines = -1
=> $m \times \frac{1}{5} = -1$
=> $m = -5$
=> Ans – (A)
Get 200 SSC mocks for just Rs. 249. Enroll here
We hope this Physics Questions for SSC CGL Exam preparation is so helpful to you.





