SSC CGL Geometry Questions
Download Top-20 Geometry questions for SSC CGL exam. Most important Geometry questions based on asked questions in previous exam papers for SSC CGL.
Download Top -20 SSC CGL geometry questions
Get 125 SSC CGL Mocks – Just Rs. 199
Take a free SSC CGL Tier-1 mock test
Download SSC CGL Tier-1 Previous Papers PDF
Question 1: A tangent is drawn to a circle of radius 6 cm from a point situated at a distance of 10 cm from the centre of the circle. The length of the tangent will be
a) 7 cm
b) 4 cm
c) 5 cm
d) 8 cm
Question 2: How many perfect squares lie between 120 and 300 ?
a) 5
b) 6
c) 7
d) 8
Question 3: A copper wire of length 36 m and diameter 2 mm is melted to form a sphere. The radius of the sphere (in cm) is:
a) 2.5
b) 3
c) 3.5
d) 4
Question 4: The product of two numbers is 45 and their difference is 4. The sum of squares of the two numbers is
a) 135
b) 240
c) 73
d) 106
Question 5: The square root of $14 + 6\sqrt{5}$
a) $2 + \sqrt{5}$
b) $3 + \sqrt{5}$
c) $5 + \sqrt{3}$
d) $3 + 2\sqrt{5}$
Question 6: A copper wire is bent in the form of an equilateral triangle, and has an area $121\sqrt{3}$ cm2 . If the same wire is bent into the form of a circle, the area(in cm2) enclosed by the wire in(Take $\pi = \frac{22}{7}$)
a) 364.5
b) 693.5
c) 346.5
d) 639.5
Question 7: The square root of 0.09 is
a) 0.30
b) 0.03
c) 0.81
d) 0.081
Question 8: If an obtuse-angled triangle ABC, is the obtuse angle and O is the orthocenter. If = 54$^{\circ}$ , then is
a) 108$^{\circ}$
b) 126$^{\circ}$
c) 136$^{\circ}$
d) 116$^{\circ}$
Question 9: If S is the circumcentre of and = 50$^{\circ}$ , then the value of is
a) 20$^{\circ}$
b) 40$^{\circ}$
c) 60$^{\circ}$
d) 80$^{\circ}$
Question 10: AC and BC are two equal cords of a circle. BA is produced to any point P and CP, when joined cuts the circle at T. Then
a) CT : TP = AB : CA
b) CT : TP = CA : AB
c) CT : CB = CA : CP
d) CT : CB = CP : CA
Question 11: The external bisectors of and of meet at point P. If = 80$^{\circ}$ , the is
a) 50$^{\circ}$
b) 40$^{\circ}$
c) 80$^{\circ}$
d) 100$^{\circ}$
Question 12: The total surface area of a sphere is $8\pi$ square unit. The volume of the sphere is
a) $\frac{8}{3}\pi$
b) $8\sqrt{3}\pi$
c) $\frac{8\sqrt{3}}{5}\pi$
d) $\frac{8\sqrt{2}}{3}\pi$
Question 13: A conical flask is full of water. The flask has base radius $r$ and height $h$. This water is poured into a cylindrical flask of base radius mr. The height of water in the cylindrical flask is
a) $\frac{h}{2} m^2$
b) $\frac{2h}{m}$
c) $\frac{h}{3m^2}$
d) $\frac{m}{2h}$
Question 14: In a triangle ABC, $\angle{A} = 90^o , \angle{C} = 55^o , \overline{AD}$ is perpendicular to $\overline{BC}$. What is the value of $\angle{BAD}$ ?
a) 60 $^{\circ}$
b) 45 $^{\circ}$
c) 55 $^{\circ}$
d) 35 $^{\circ}$
Question 15: If G is the centroid of triangle ABC and area of triangle ABC = 48cm2, then the area of triangle BGC is
a) 8 cm2
b) 16 cm2
c) 24 cm2
d) 32 cm2
Get 125 SSC CGL Mocks – Just Rs. 199
Question 16: The diagonals AC and BD of a cyclic quadrilateral ABCD intersect each other at the point P. Then, it is always true that
a) AP . CP = BP . DP
b) AP . BP = CP . DP
c) AP . CD = AB . CP
d) BP . AB = CD . CP
Question 17: A, B, C, D are four points on a circle. AC and BD intersect at a point such that $\angle{BEC} = 130^o$ and $\angle{ECD} = 20^o$. Then, $\angle{BAC}$ is
a) 90 $^{\circ}$
b) 100 $^{\circ}$
c) 110 $^{\circ}$
d) 120 $^{\circ}$
Question 18: In a triangle, if three altitudes are equal, then the triangle is
a) equilateral
b) right
c) isosceles
d) obtuse
Question 19: ABCD is a cyclic trapezium with AB || DC and AB = diameter of the circle. If angleCAB = $30^{\circ}$, then angleADC is
a) $60^{\circ}$
b) $120^{\circ}$
c) $150^{\circ}$
d) $30^{\circ}$
Question 20: ABC is a triangle. The bisectors of the internal angle $\angle$B and external $\angle$C intersect at D. If $\angle$BDC=$50^{\circ}$, then $\angle$A is
a) $100^{\circ}$
b) $90^{\circ}$
c) $120^{\circ}$
d) $60^{\circ}$
Join Exam Preparation Telegram Group
More SSC CGL Important Questions and Answers PDF
Answers & Solutions:
1) Answer (D)
radius OA = 6 and OB = 10
Now, in $\triangle$OAB right angle at A
AB = $\sqrt{(OB)^2 – (OA)^2}$
= $\sqrt{100-36} = \sqrt{64}$
= 8 cm
2) Answer (C)
let’s say n be a number whose perfect square lie between 120 and 300
hence 120<$n^{2}$<300
or $121\leq n^{2} \leq289$
or $11\leq n^{2} \leq17$
3) Answer (B)
since we know volume will remain same while melting
$\pi r_{1}^{2}h= \frac{4}{3}\pi r_{2}^{3}$
where $r_{1}$ is radius of cylinderical wire and $r_{2}$ is radius of sphere and h is length of wire
putting values we will get $r_{2}$ = 3 cm.
4) Answer (D)
As we know $(a-b)^{2}$ = $a^{2} + b^{2} – 2ab$
We assume that first number is a and second number is b hence ab = 45
and a – b = 4
after putiing values we will get $a^{2} + b^{2}$ = 106
5) Answer (B)
Given question can be written as $9+5+6\sqrt{5}$
or it will be square of $3+\sqrt{5}$
6) Answer (C)
Area of equilateral triangle is $\frac{\sqrt{3}}{4} a^{2}$ where a is side of triangle
which is equals to $121{\sqrt{3}}$
or a = 22 and whole length of wire will be 66
from here when it is bend to make a circle, circumference will be $2\pi r$ = 66
r = 10.5
hence area of circle will be $\pi r^{2}$ = 346.5
7) Answer (A)
0.09 = $\frac{9}{100}$
$\sqrt{\frac{9}{100}} = \frac{3}{10}$ = 0.3
8) Answer (B)
9) Answer (B)
10) Answer (C)
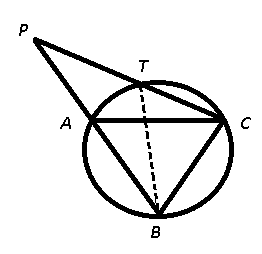
It is given that AC = BC, also $\triangle$ PTB and $\triangle$ PAC are similar, we have :
$\frac{CA}{CP}=\frac{BT}{BP}$ —————-(i)
Also, we have $\angle$ PBC = $\angle$ BTC ($\because$ $\angle$ PBC = $\angle$ BAC = $\angle$ BTC) and $\angle$ PCB = $\angle$ BCT
=> $\triangle$ PBC $\sim$ $\triangle$ BTC
Thus, $\frac{CB}{BP}=\frac{CT}{BT}$
=> $\frac{BT}{BP}=\frac{CT}{CB}$ ————–(ii)
From equations (i) and (ii), we get :
$\frac{CA}{CP}=\frac{CT}{CB}$
=> Ans – (C)
18000+ Questions – Free SSC Study Material
11) Answer (A)
12) Answer (D)
Let the radius of the sphere be ‘r’
Hence $4\pi r^2$ = $8\pi$
=> r = $\sqrt{2}$
Volume of the cube = $\frac{4}{3}\pi r^3$ = $\frac{4}{3}\pi \sqrt{2}^3$ = $\frac{8\sqrt{2}}{3}\pi$
13) Answer (C)
Volume of water in flask = $\frac{\pi r^2 h}{3}$ (where h is height of water in conical flask)
Volume of water in cylinder = $\pi m^2r^2 h_1$ (where h_1 is height of water in cylinderical flask)
Hence now $\frac{\pi r^2 h}{3}$ = $\pi m^2r^2 h_1$
or $h_1 = \frac{h}{3m^2}$
14) Answer (C)
$\angle A = 90^o$
$\angle C = 55^o$
$\angle B$ will be $180 – (90+55) = 35^o$
As AD is perpendicular to BC Hence $\angle BAD=180-(90+35)=55^o$
15) Answer (B)
As we know area of triangle, with centroid as one of the vertices and remaining 2 triangle vertices, is $\frac{1}{3}$rd of the area of whole triangle.
Hence area will be $\frac{48}{3}$ = 16
16) Answer (A)
As we know that a cyclic quadrilateral can be inscribed into a circle, Hence in triangle APB and in triangle CPD.
$\angle PAB = \angle PDC$ (same sector angles)
$\angle PCD = \angle PBA$ (same sector angles)
Hence third angle will also be equal and they will be similar triangles.
So $\frac{AP}{PD} = \frac{BP}{PC}$
Get 125 SSC CGL Mocks – Just Rs. 199
18000+ Questions – Free SSC Study Material
17) Answer (C)
Angle ABD will be equal to angle ACD = $20^o$ (same sector angles)
Angle BEC = $130^o$ so angle AED = $130^o$ (concurrent angles)
Now angle BEA will be $\frac{360-130-130}{2} = 50^o$
So angle EDC will be $180-(50+20) = 110^o$
18) Answer (A)
It is property of equilateral triangle that length of all its altitutes are equal.
19) Answer (B)
let angle CDA = x
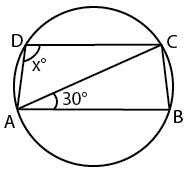
since AB is parallel to CD, angle ACD=30 and angle CAD=30
in triangle ACD,
sum of all three angles = 180
30 + 30 + x = 180
x = 120
so the answer is option B.
20) Answer (A)
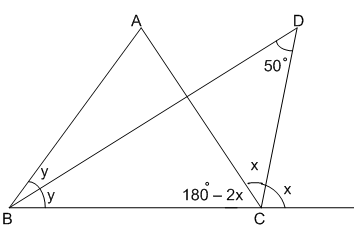
In $\triangle$ BDC,
=> $y+(180^\circ-2x+x)+50^\circ=180^\circ$
=> $y-x+50^\circ=0$
=> $y-x=-50^\circ$
In $\triangle$ ABC,
=> $2y+(180^\circ-2x)+\angle A=180^\circ$
=> $2(y-x)+\angle A=0$
=> $2(-50^\circ)+\angle A=0$
=> $\angle A=100^\circ$
=> Ans – (A)






